习题课讲解

12.3 习题课讲解

12.3.1 一阶微分方程

例 12.3.1 画出以下微分方程的斜率场的大致图像，并根据斜率场的特点说明方程的解的特征：

(1): $y^{'} = x (1 - x)$
(2): $y^{'} = \frac{y}{1 + y^{2}}$
(3): $y^{'} = \frac{x - y}{x + y}$
(4): $y^{'} = \sin (x^{2} + y^{2})$

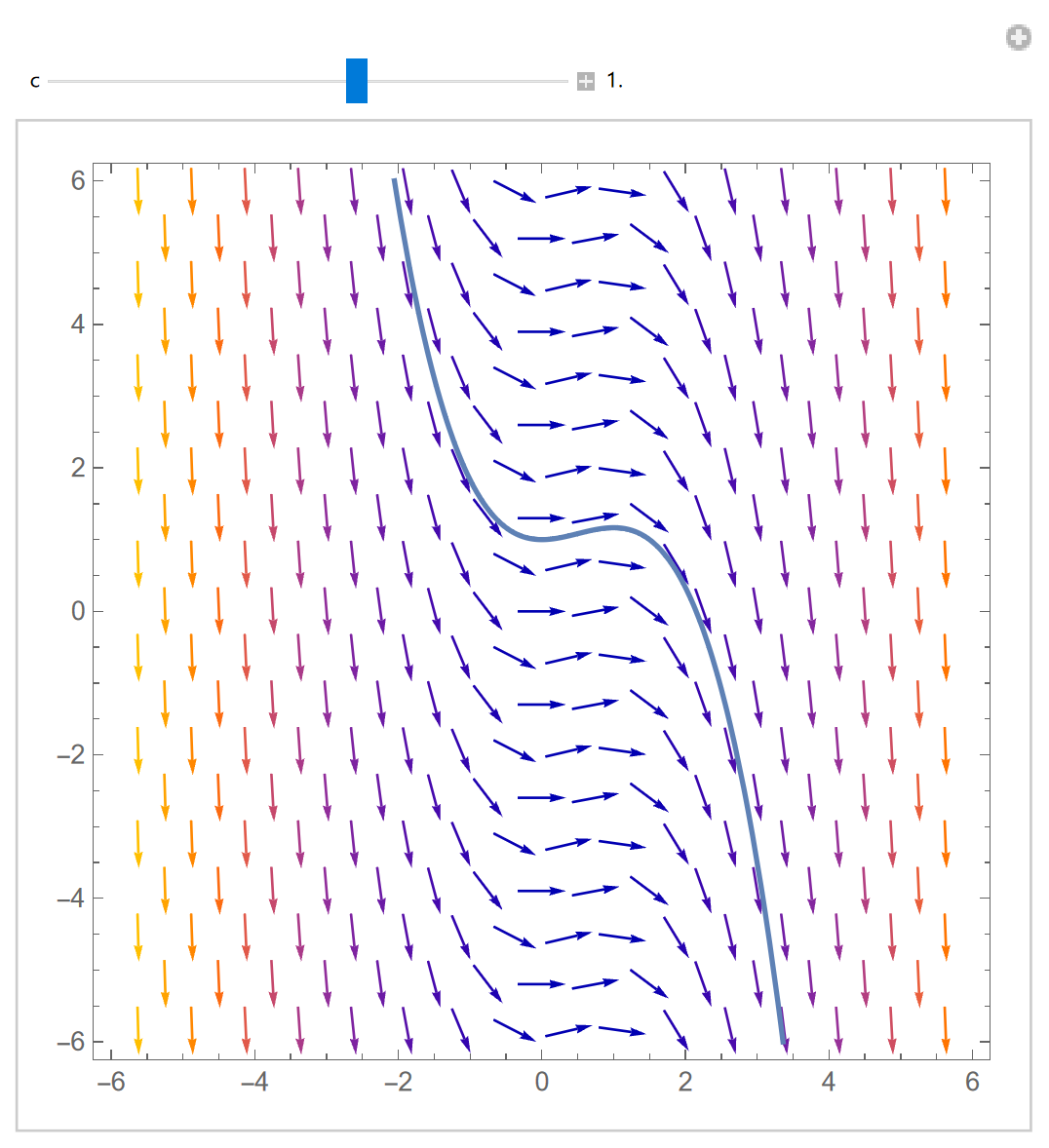
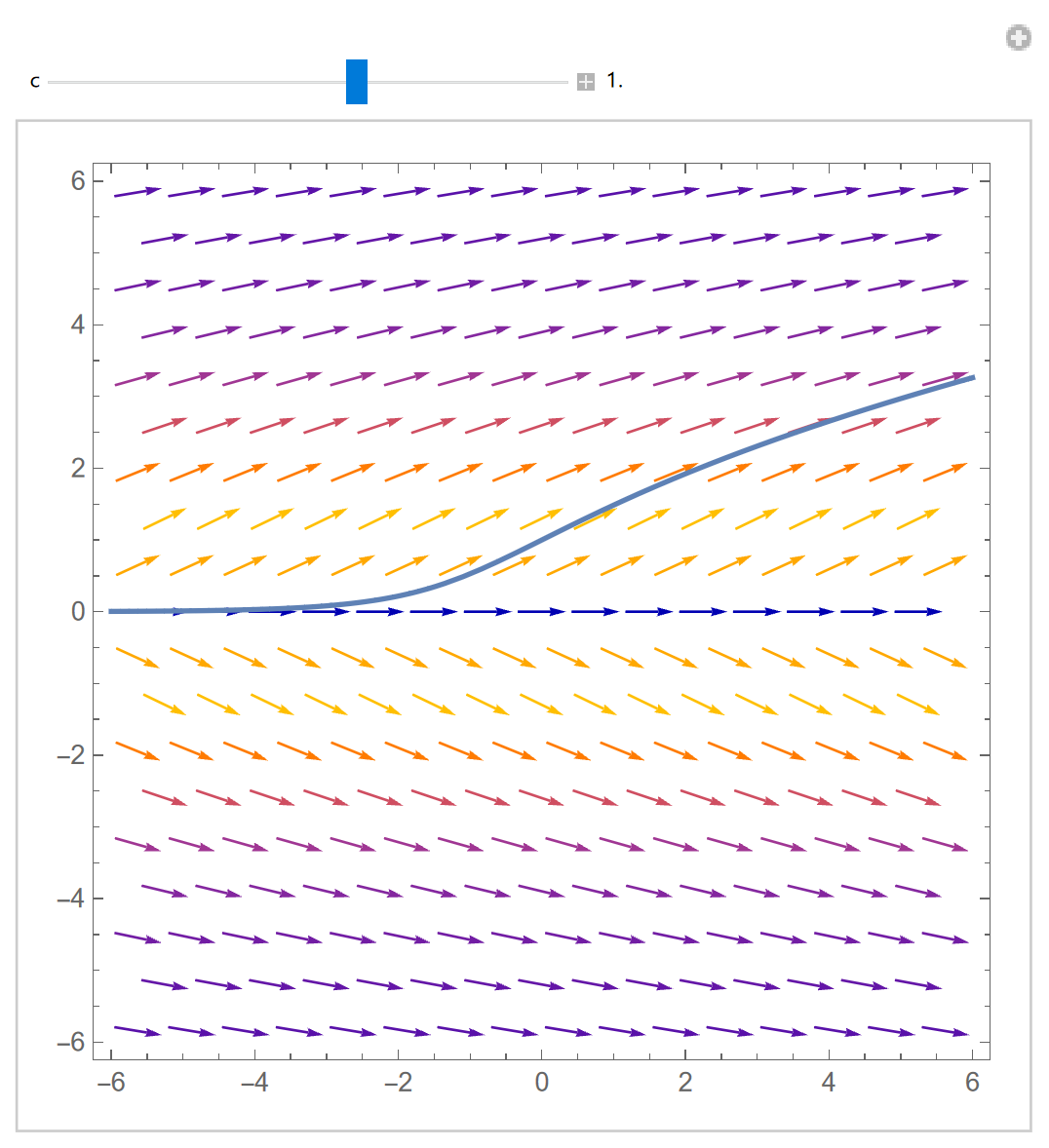
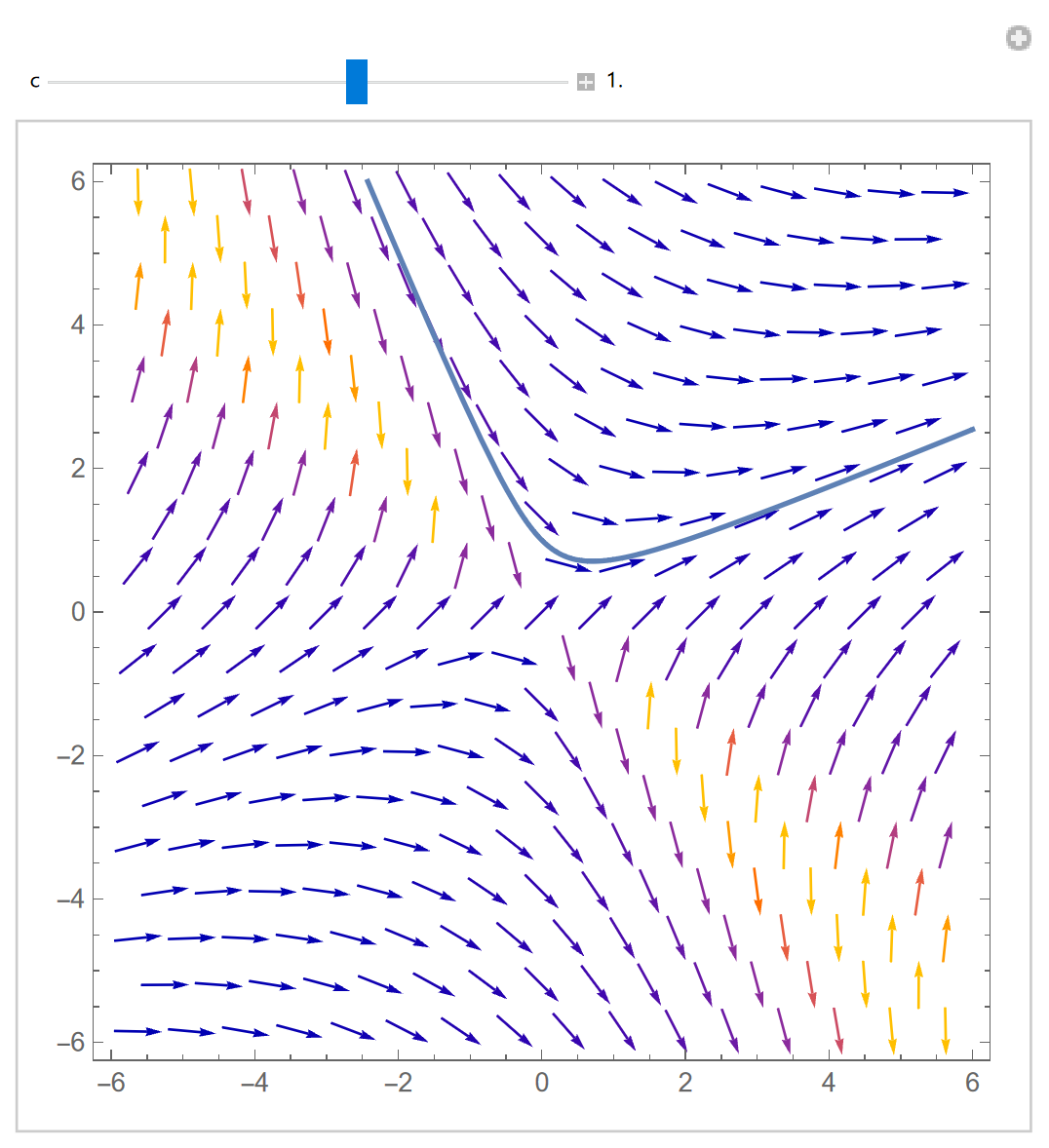
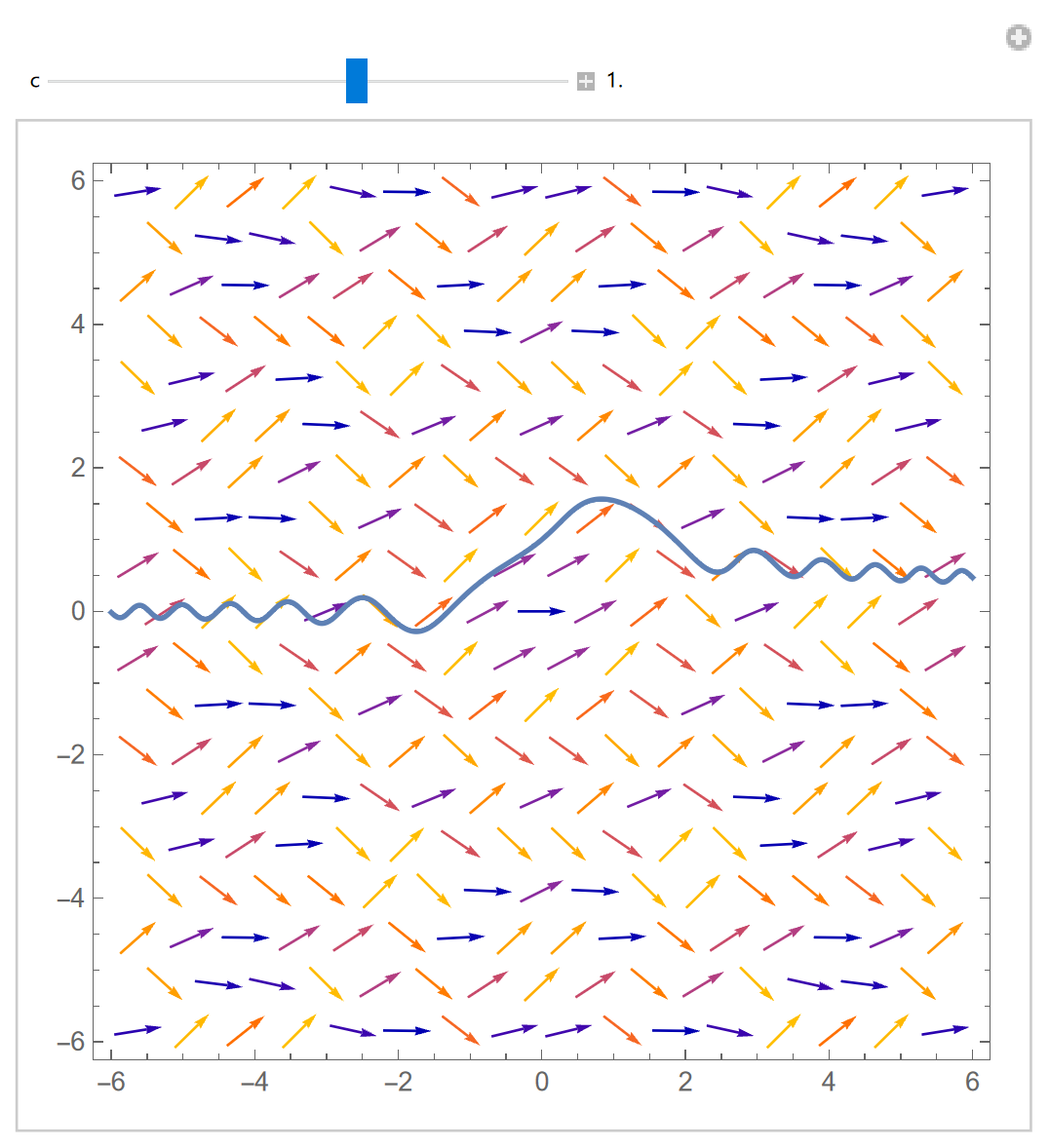
解利用Mathematica绘制的斜率场如图12.3.1所示。斜率场的特征为：

(1): $y^{'} = f (x, y) = g (x)$ 的斜率场只与 $x$ 有关，故将某条积分曲线沿 $y$ 轴平移后，其仍为积分曲线。
(2): $y^{'} = f (x, y) = g (y)$ 的斜率场只与 $y$ 有关，故将某条积分曲线沿 $x$ 轴平移后，其仍为积分曲线。
(3): 对于 $y^{'} = f (x, y) = g (\frac{y}{x})$ 的斜率场，注意到 $f (a x, a y) = f (x, y)$ ，故将某条积分曲线沿原点作伸缩变换后，其仍为积分曲线。
(4): 对于 $y^{'} = f (x, y) = g (x^{2} + y^{2})$ 的斜率场，其在以原点为中心的同心圆上保持不变，故将某条积分曲线绕原点旋转后，其仍为积分曲线。

◻

例 12.3.2 求以下微分方程的通解：

(1): $y^{'} = x (1 - x)$
(2): $y^{'} = \frac{y}{1 + y^{2}}$
(3): $y^{'} = \frac{x - y}{x + y}$
(4): $y^{'} = (x + y + 3)^{2}$

解

(1): $y^{'} = x (1 - x)$ ，分离变量得 $\begin{matrix} (1) & \frac{d y}{d x} = x - x^{2} ⟹ y = \frac{x^{2}}{2} - \frac{x^{3}}{3} + C \end{matrix}$
(2): $y^{'} = \frac{y}{1 + y^{2}}$ ，分离变量得 $\begin{matrix} (2) & \frac{d x}{d y} = \frac{1 + y^{2}}{y} ⟹ x = \frac{y^{2}}{2} + \ln | y | + C \end{matrix}$ 此即方程的通解。当 $y > 0$ （或 $y < 0$ ）时 $x_{y}^{'} > 0$ （或 $x_{y}^{'} < 0$ ），所以 $x = x (y)$ 有可微的反函数 $y = y (x)$ 。此外，方程还有特解 $y = 0$ 。
(3): $y^{'} = \frac{x - y}{x + y}$ ，令 $u = \frac{y}{x}$ ，则 $\begin{matrix} (3) & x \frac{d u}{d x} = \frac{1 - u}{1 + u} - u = \frac{1 - 2 u - u^{2}}{1 + u} \end{matrix}$ 因此 $\begin{matrix} (4) & d \ln | x | = \frac{d x}{x} = \frac{(1 + u) d u}{1 - 2 u - u^{2}} = - \frac{1}{2} d \ln | u^{2} + 2 u - 1 | \end{matrix}$ 两边积分可得 $\begin{matrix} (5) & \ln | u^{2} + 2 u - 1 | + 2 \ln | x | = C ⟹ y^{2} + 2 x y - x^{2} = C \end{matrix}$
(4): $y^{'} = (x + y + 3)^{2}$ ，令 $u = x + y + 3$ ，则 $\begin{matrix} (6) & \frac{d u}{d x} = \frac{d y}{d x} + 1 = 1 + u^{2} ⟹ \frac{d u}{1 + u^{2}} = d x \end{matrix}$ 两边积分可得 $\begin{matrix} (7) & \arctan u = x + C ⟹ \arctan (x + y + 3) = x + C \end{matrix}$

◻

注

(1): 一阶微分方程 $F (x, y, y^{'}) = 0$ 的解允许是由代数方程 $G (x, y) = C$ 表示的曲线，函数 $G$ 叫做微分方程的首次积分，物理上它是一个守恒量。
(2): 微分方程具有的对称性（变换下的不变性）意味着它存在某种形式的首次积分，即某种守恒量。
(3): 可以利用微分方程的对称性得到求解微分方程的方法。

例 12.3.3 求下列方程的解：

(1): $y^{'} = \frac{x (y - 1)}{y + x y}$
(2): $y^{'} = \sqrt{x y}$
(3): $(1 + e^{x}) y y^{'} = e^{x}, y (1) = 1$
(4): $(1 - x) d y = (1 + y) d x$
(5): $3 x d y - y (2 - x \cos x) d x = 0$
(6): $(e^{x + y} - e^{x}) d x + (e^{x + y} + e^{y}) d y = 0$

解这些方程都是可分离变量的方程，故此处仅列出答案。

(1): $(y - 1) (x + 1) e^{y - x} = C$
(2): $y = {(\frac{1}{3} x^{3 / 2} + C)}^{2}$
(3): $y = \sqrt{2 \ln (1 + e^{x}) + 1 - 2 \ln (1 + e)}$
(4): $(1 + y) (1 - x) = C$
(5): $y = C x^{2 / 3} e^{- \sin x}$
(6): $(e^{x} + 1) (e^{y} - 1) = C$

◻

例 12.3.4 平面直角坐标系中，与 $y$ 轴平行的光线经曲线 $y = y (x)$ 反射后汇聚于原点。求曲线的方程。

解曲线的切向量为 $t = (1, y^{'})$ ，法向量为 $n = (- y^{'}, 1)$ 。假设光沿 $y$ 轴负方向入射，则入射光的单位方向向量为 $a = (0, - 1)$ ，反射光的单位方向向量为 $\begin{matrix} (8) & b = \frac{(- x, - y)}{\sqrt{x^{2} + y^{2}}} \end{matrix}$ 由反射定律可得 $\begin{matrix} (9) & n \cdot b = - n \cdot a ⟹ 1 = \frac{x y^{'} - y}{\sqrt{x^{2} + y^{2}}} ⟹ y^{'} = \frac{y}{x} + \sqrt{1 + {(\frac{y}{x})}^{2}} \end{matrix}$ 令 $u = \frac{y}{x}$ ，则 $\begin{matrix} (10) & x \frac{d u}{d x} = u + \sqrt{1 + u^{2}} - u ⟹ \frac{d u}{\sqrt{1 + u^{2}}} = \frac{d x}{x} \end{matrix}$ 两边积分可得 $\begin{matrix} (11) & \ln | u + \sqrt{1 + u^{2}} | = \ln | x | + C ⟹ u + \sqrt{1 + u^{2}} = C x \end{matrix}$ 解得 $\begin{matrix} (12) & u = \frac{(C x)^{2} - 1}{2 C x} ⟹ y = \frac{C}{2} x^{2} - \frac{1}{2 C} \end{matrix}$ 即为抛物线。 $◻$

例 12.3.5 求曲线族 $x y = C$ 的正交曲线族。

解该曲线族满足的微分方程为 $\begin{matrix} (13) & y d x + x d y = 0 \end{matrix}$ 由此可得该曲线族的正交向量场为 $(y, x)$ ，它应当为正交曲线族的切向量场，因此 $\begin{matrix} (14) & x d x - y d y = 0 ⟹ x^{2} - y^{2} = C \end{matrix}$ $◻$

12.3.2 一阶线性方程

例 12.3.6 记 $P_{α, n}$ 是所有形如 $e^{α x} P (x)$ 的拟多项式组成的线性空间，其中 $P$ 是次数不超过 $n$ 的多项式。证明：

(1): 设 $λ \in R$ ，若 $α \neq λ$ ，则 $\forall f \in P_{α, n}$ ， $y^{'} - λ y = f$ 在 $P_{α, n}$ 中有唯一解。
(2): $\forall f \in P_{λ, n}$ ， $y^{'} - λ y = f$ 在 $P_{λ, n + 1}$ 中有无穷多解，这些解彼此相差 $e^{λ x}$ 的一个常数倍数。

证明 (1) 记 $L = \frac{d}{d x} - λ$ ，则 $\begin{matrix} (15) & L (e^{α x} \frac{x^{k}}{k!}) = e^{α x} [(α - λ) \frac{x^{k}}{k!} + \frac{x^{k - 1}}{(k - 1)!}] \end{matrix}$ 因此 $L$ 是 $P_{α, n}$ 到自身的线性变换，在基 $\begin{matrix} (16) & {e^{α x}, e^{α x} x, \dots, e^{α x} \frac{x^{n}}{n!}} \end{matrix}$ 下的表示矩阵为 $\begin{matrix} (17) & A = {(\begin{matrix} α - λ & 1 \\ α - λ & 1 \\ ⋱ & ⋱ \\ α - λ & 1 \\ α - λ \end{matrix})}_{(n + 1) \times (n + 1)} \end{matrix}$ 当 $α \neq λ$ 时， $A$ 可逆，从而 $L$ 是 $P_{α, n}$ 到自身的可逆线性变换。

(2) $L : P_{λ, n + 1} \to P_{λ, n}$ 的矩阵表示为 $(0, I_{n + 1})_{(n + 1) \times (n + 2)}$ ，所以 $L$ 是满射、但不是单射，所以 $\forall f \in P_{λ, n}$ ， $y^{'} - λ y = f$ 在 $P_{λ, n + 1}$ 中有无穷多解，这些解彼此相差 $c \cdot e^{λ x}$ 。 $◻$

例 12.3.7 求下列方程的解：

(1): $y^{'} - 2 y = e^{x} x^{2}$
(2): $y^{'} + y = \sin x$
(3): $y^{'} - y = x e^{x}$

解 (1) 齐次方程的通解为 $y = C e^{2 x}$ 。设 $\begin{matrix} (18) & y = c \cdot (e^{x}, e^{x} x, e^{x} \frac{x^{2}}{2}) \end{matrix}$ 由此可得 $\begin{matrix} (19) & (\begin{matrix} - 1 & 1 & 0 \\ 0 & - 1 & 1 \\ 0 & 0 & - 1 \end{matrix}) c = (\begin{matrix} 0 \\ 0 \\ 2 \end{matrix}) ⟹ c = (\begin{matrix} - 2 \\ - 2 \\ - 2 \end{matrix}) ⟹ y (x) = - e^{x} (2 + 2 x + x^{2}) \end{matrix}$ 由此得到非齐次方程的特解。因此非齐次方程的通解为 $\begin{matrix} (20) & y = C e^{2 x} - e^{x} (2 + 2 x + x^{2}) \end{matrix}$

(2) 齐次方程的通解为 $y = C e^{- x}$ 。注意到 $\begin{matrix} (21) & \begin{aligned} L (\sin x) & = \cos x + \sin x \\ L (\cos x) & = - \sin x + \cos x \end{aligned} \end{matrix}$ 因此 $\begin{matrix} (22) & \sin x = L (\frac{\sin x - \cos x}{2}) ⟹ y = \frac{\sin x - \cos x}{2} \end{matrix}$ 由此得到非齐次方程的特解。因此非齐次方程的通解为 $\begin{matrix} (23) & y = C e^{- x} + \frac{\sin x - \cos x}{2} \end{matrix}$

(3) 齐次方程的通解为 $y = C e^{x}$ 。注意到 $\begin{matrix} (24) & L (e^{x} \frac{x^{2}}{2}) = e^{x} x \end{matrix}$ 由此得到非齐次方程的特解。因此非齐次方程的通解为 $\begin{matrix} (25) & y = C e^{x} + e^{x} \frac{x^{2}}{2} \end{matrix}$ $◻$

例 12.3.8 求下列方程的解：

(1): $y^{'} + 2 x y = 2 x^{3} y^{2}$
(2): $y^{'} = a y^{2} + \frac{b}{x^{2}}, 4 a b > 1$

解 (1) 这是Bernoulli方程。令 $z = y^{1 - 2} = y^{- 1}$ ，则 $\begin{matrix} (26) & z^{'} = - y^{- 2} y^{'} = - y^{- 2} (2 x^{3} y^{2} - 2 x y) = - 2 x^{3} + 2 x z \end{matrix}$ 解得 $\begin{matrix} (27) & z = C e^{x^{2}} + x^{2} + 1 ⟹ y = \frac{1}{C e^{x^{2}} + x^{2} + 1} \end{matrix}$ 此外， $y = 0$ 也是方程的解。

(2) 这是Riccati方程的特例。令 $z = \frac{1}{y}$ ，则 $\begin{matrix} (28) & z^{'} = - y^{- 2} y^{'} = - y^{- 2} (a y^{2} + \frac{b}{x^{2}}) = - a - b {(\frac{z}{x})}^{2} \end{matrix}$ 设 $Δ = 4 a b - 1$ ，由此解得 $\begin{matrix} (29) & z = \frac{- 1 + \sqrt{Δ} \tan \frac{\sqrt{Δ} (C_{1} - \ln x)}{2}}{2 b} x = \frac{1}{y} \end{matrix}$ $◻$