第九次作业参考答案

13.1 第九次作业参考答案

13.1.1 习题8.2

例 13.1.1 （习题8.2.1）求区间 $[0, + \infty)$ 上的可微函数 $f$ 使得 $\begin{matrix} (1) & \ln | f (x) | + \int_{0}^{x} f (t) d t = 0 \end{matrix}$

解令 $x = 0$ 可得 $\begin{matrix} (2) & \ln | f (0) | = 0 ⟹ f (0) = \pm 1 \end{matrix}$ 由于 $f$ 可微，对积分方程两边求导可得 $\begin{matrix} (3) & \frac{f^{'} (x)}{f (x)} + f (x) = 0 ⟹ - \frac{d f}{f^{2}} = d x \end{matrix}$ 两边积分可得 $\begin{matrix} (4) & \frac{1}{f (x)} = x + C ⟹ f (x) = \frac{1}{x + C} \end{matrix}$ 由 $f (0) = \pm 1$ 可得 $C = \pm 1$ ； $C = - 1$ 需要舍去，因为此时 $f (x)$ 在 $x = 1$ 处间断。因此 $f (x) = \frac{1}{x + 1}$ 。 $◻$

例 13.1.2 （习题8.2.2）求解微分方程 $y^{'} = 2 x y^{2}$ ，并回答以下问题：

(1): 证明： $\forall x_{0} \in R$ 、 $\forall y_{0} \neq 0$ ，该方程存在唯一解满足初始条件 $y (x_{0}) = y_{0}$ ，且在它的定义域中总有 $y (x) \neq 0$ ；
(2): 对(1)中的解 $y (x)$ ，求它的定义域；
(3): 证明： $\forall x_{0}, y_{0} \in R$ ，该方程有唯一解满足初始条件 $y (x_{0}) = y_{0}$ 。
(4): 写出该方程的通解，并证明通解并非该方程的全部解。

注在讨论微分方程的解时，我们通常只在解的存在区间上关注解的性质（存在性、唯一性、适定性）。

引理 13.1.3 设 $f$ 在区间 $[a, b]$ 上单调不减且满足 $f (a) = 0$ 、 $f (b) > 0$ 。证明： $\exists ξ \in [a, b)$ 使得 $(\forall x < ξ) f (x) = 0$ 且 $(\forall x > ξ) f (x) > 0$ 。

证明令 $[a_{0}, b_{0}] = [a, b]$ ，考虑 $ξ_{n} = \frac{a_{n} + b_{n}}{2}$ ：

若 $f (ξ_{n}) = 0$ 则令 $a_{n + 1} = ξ_{n}$ ，即 $f (a_{n + 1}) = 0$ ；
若 $f (ξ_{n}) > 0$ 则令 $b_{n + 1} = ξ_{n}$ ，即 $f (b_{n + 1}) > 0$ 。

由有界闭区间套定理以及 $lim_{n \to + \infty} (b_{n} - a_{n}) = 0$ 知 $⋂_{n = 0}^{\infty} [a_{n}, b_{n}] = {ξ}$ 且 $ξ = lim_{n \to + \infty} a_{n} = lim_{n \to + \infty} b_{n}$ ，此时

$\forall x < ξ$ ， $\exists N > 0$ 使得 $n > N ⟹ x < a_{n} ⟹ f (x) \leq f (a_{n}) = 0$ ；
$\forall x > ξ$ ， $\exists N > 0$ 使得 $n > N ⟹ x > b_{n} ⟹ f (x) \geq f (b_{n}) > 0$ 。

故引理成立。进一步地，若 $f$ 连续，则 $\begin{matrix} (5) & f (ξ) = f (lim_{n \to + \infty} a_{n}) = lim_{n \to + \infty} f (a_{n}) = 0 \end{matrix}$ $◻$

解 (1) 设 $y$ 在区间 $I \subseteq R$ 上恒有定义且 $x_{0} \in I$ ，此时 $I$ 连通，下面我们只在 $I$ 上考虑 $y (x)$ 。首先证明：（结论I）若 $y (x) \neq 0$ ，则该方程存在唯一解满足 $y (x_{0}) = y_{0}$ 。考虑函数 $\begin{matrix} (6) & g (x) = \frac{1}{y (x)} + x^{2} ⟹ g^{'} (x) = 0 \end{matrix}$ 由Lagrange中值定理可得 $\forall x \in I$ 且 $x \neq x_{0}$ ，存在 $x, x_{0}$ 之间的 $ξ$ 满足 $\begin{matrix} (7) & g (x) - g (x_{0}) = g^{'} (ξ) (x - x_{0}) = 0 ⟹ y (x) = \frac{1}{\frac{1}{y_{0}} + x_{0}^{2} - x^{2}} \end{matrix}$ 因此原方程具有唯一解，且此解满足 $y (x) \neq 0$ 。

然后证明：（结论II）若 $y_{0} \neq 0$ 且 $0 \notin I$ ，则 $y (x) \neq 0$ 。当 $0 \notin I$ 时 $y$ 具有单调性，故不妨设 $y_{0} > 0$ 且 $y$ 在 $I$ 上单调不减。假设 $\exists ξ \in I$ 使得 $y (ξ) = 0$ ，则 $ξ < x_{0}$ ，由引理知 $\exists η \in [ξ, x_{0})$ 满足 $y (η) = 0$ 且 $(\forall x > η) y (x) > 0$ ，在 $[η, x_{0})$ 上应用结论I可知原方程有唯一解 $y (x) = \frac{1}{\frac{1}{y_{0}} + x_{0}^{2} - x^{2}}$ ，然而此时 $y (η) \neq 0$ ，矛盾！故 $y (x) \neq 0$ 。

最后证明：（结论III）若 $y_{0} \neq 0$ ，则 $y (x) \neq 0$ 。结论II已证明 $0 \notin I$ 的情况；当 $0 \in I$ 时，分别在 $I \cap (- \infty, 0]$ 和 $I \cap [0, + \infty)$ 上应用结论II可知 $y (x) \neq 0$ 。

综上所述，由结论III和结论I可知原方程具有唯一解，且此解满足 $y (x) \neq 0$ 。

(2) 当 $\frac{1}{y_{0}} + x_{0}^{2} < 0$ ，即当 $x = 0$ 且 $y < 0$ 、 $x \neq 0$ 且 $- \frac{1}{x^{2}} < y < 0$ 时， $y (x)$ 的定义域为 $R$ ；当 $\frac{1}{y_{0}} + x_{0}^{2} \geq 0$ ，即当 $y > 0$ 、 $x \neq 0$ 且 $y \leq - \frac{1}{x^{2}}$ 时，记 $c_{0} = \sqrt{\frac{1}{y_{0}} + x_{0}^{2}}$ ， $y (x)$ 的定义域为 $(- \infty, - c_{0}) \cup (c_{0}, + \infty)$ 。

(3) 若 $y_{0} = 0$ ，假设 $\exists ξ \in I$ 使得 $y (ξ) \neq 0$ ，由(1)可知 $(ξ, y (ξ))$ 确定了唯一解 $y (x)$ ，然而此时 $y (x_{0}) \neq 0$ ，矛盾！故 $y (x) = 0$ ，亦是原方程的唯一解。

(4) 由题可得 $\begin{matrix} (8) & \frac{d y}{y^{2}} = 2 x d x ⟹ - \frac{1}{y} = x^{2} + C ⟹ y = - \frac{1}{x^{2} + C} \end{matrix}$ 为原方程的通解；此外方程还有特解 $y = 0$ ，其并不包含在通解中。 $◻$

另解解的唯一性可直接利用Grönwall不等式证明，参考例14.2.4。 $◻$

例 13.1.4 （习题8.2.3）讨论以下微分方程初值问题解的存在性与唯一性，以及解的定义域： $\begin{matrix} (9) & {\begin{cases} y^{'} = \sqrt{y} \\ y (x_{0}) = y_{0} \end{cases} \end{matrix}$

解利用分离变量法求解微分方程可得 $\begin{matrix} (10) & \frac{d y}{\sqrt{y}} = d x ⟹ 2 \sqrt{y} = x + C ⟹ y = {(\frac{x + C}{2})}^{2} \end{matrix}$ 然而此时方程出现增解，代入原方程可得 $\begin{matrix} (11) & \frac{x + C}{2} = \sqrt{{(\frac{x + C}{2})}^{2}} ⟹ x \geq - C \end{matrix}$ 由于 $\sqrt{y}$ 需满足 $y \geq 0$ ，故当 $y_{0} < 0$ 时原方程无解。当 $y_{0} > 0$ 时，由题可得 $\begin{matrix} (12) & y_{0} = {(\frac{x_{0} + C}{2})}^{2} ⟹ C = \pm 2 \sqrt{y_{0}} - x_{0} \end{matrix}$ $C = - 2 \sqrt{y_{0}} - x_{0}$ 需要舍去，因为此时 $x_{0}$ 不在定义域 $[- C, + \infty)$ 中。故当 $y_{0} > 0$ 时原方程具有唯一解，且定义域为 $(x_{0} - 2 \sqrt{y_{0}}, + \infty)$ 。

此外方程还有特解 $y = 0$ ，其并不包含在通解中。故当 $y_{0} = 0$ 时，方程有无数个解¹；除了 $y = 0$ 以外，它们具有以下形式： $\begin{matrix} (13) & y = {\begin{cases} 0 & x \leq ξ \\ {(\frac{x - ξ}{2})}^{2} & x > ξ \end{cases} \end{matrix}$ 其中 $ξ$ 是任意不小于 $x_{0}$ 的实数。 $◻$

例 13.1.5 （习题8.2.4）设 $P (x, y), Q (x, y)$ 都是 $k$ 次齐次函数，即 $\forall λ > 0$ 、 $\forall (x, y) \neq (0, 0)$ ，都有 $\begin{matrix} (14) & P (λ x, λ y) = λ^{k} P (x, y), Q (λ x, λ y) = λ^{k} Q (x, y) \end{matrix}$ 因此在 $x y$ 坐标平面中沿从原点出发的每条射线平移，微分方程 $\begin{matrix} (15) & P (x, y) d x + Q (x, y) d y = 0 \end{matrix}$ 对应的方向场保持不变。证明：在平面极坐标系下，上述微分方程是分离变量的。

证明作极坐标换元 $(x, y) = (r \cos θ, r \sin θ)$ 可得 $\begin{matrix} (16) & {\begin{cases} d x = \cos θ d r - r \sin θ d θ \\ d y = \sin θ d r + r \cos θ d θ \end{cases} ⟹ (\begin{matrix} d x \\ d y \end{matrix}) = (\begin{matrix} \cos θ & - \sin θ \\ \sin θ & \cos θ \end{matrix}) (\begin{matrix} d r \\ r d θ \end{matrix}) \end{matrix}$ 故有 $\begin{matrix} (17) & \begin{aligned} 0 & = P (x, y) d x + Q (x, y) d y = (\begin{array}{c} P (x, y) & Q (x, y) \end{array}) (\begin{array}{c} d x \\ d y \end{array}) \\ = (\begin{array}{c} P (r \cos θ, r \sin θ) & Q (r \cos θ, r \sin θ) \end{array}) (\begin{array}{c} \cos θ & - \sin θ \\ \sin θ & \cos θ \end{array}) (\begin{array}{c} d r \\ r d θ \end{array}) \\ = r^{k} \underset{(M (θ) N (θ))}{\underset{⏟}{(\begin{array}{c} P (\cos θ, \sin θ) & Q (\cos θ, \sin θ) \end{array}) (\begin{array}{c} \cos θ & - \sin θ \\ \sin θ & \cos θ \end{array})}} (\begin{array}{c} d r \\ r d θ \end{array}) \\ = r^{k} (\begin{array}{c} M (θ) & N (θ) \end{array}) (\begin{array}{c} d r \\ r d θ \end{array}) = r^{k} (M (θ) d r + N (θ) r d θ) \end{aligned} \end{matrix}$ 故原方程可化为如下变量分离形式 $\begin{matrix} (18) & \frac{d r}{r} + \frac{N (θ)}{M (θ)} d θ = 0 \end{matrix}$ $◻$

例 13.1.6 （习题8.2.7）求解以下微分方程： $\begin{matrix} (19) & y^{'} = \frac{x^{2} (y - 2 x^{3})}{2 y + 3 x^{3}} \end{matrix}$

解原方程可化为 $\begin{matrix} (20) & x {(\frac{y}{x^{3}})}^{'} + 3 \frac{y}{x^{3}} = \frac{y^{'}}{x^{2}} = \frac{\frac{y}{x^{3}} - 2}{2 \frac{y}{x^{3}} + 3} \end{matrix}$ 作换元 $p = \frac{y}{x^{3}}$ 可得 $\begin{matrix} (21) & x p^{'} = \frac{p - 2}{2 p + 3} - 3 p = - \frac{2 (1 + p) (1 + 3 p)}{2 p + 3} ⟹ (\frac{7}{1 + 3 p} - \frac{1}{1 + p}) d p + 4 \frac{d x}{x} = 0 \end{matrix}$ 两边积分可得 $\begin{matrix} (22) & \frac{7}{3} \ln | 1 + 3 p | - \ln | 1 + p | + 4 \ln | x | = \frac{1}{3} \ln | \frac{(1 + 3 p)^{7} x^{12}}{(1 + p)^{3}} | = \tilde{C} \end{matrix}$ 故原方程的通解为 $\begin{matrix} (23) & {(3 y + x^{3})}^{7} = C {(y + x^{3})}^{3} \end{matrix}$ 由此得到隐函数形式的通解。 $◻$

例 13.1.7 （习题8.2.8）考虑二阶微分方程 $\begin{matrix} (24) & \frac{y^{″}}{1 + y^{' 2}} + a \frac{x y^{'} - y}{x^{2} + y^{2}} = 0 \end{matrix}$

(1): 考虑坐标变换 $(ξ, η) = (λ x, λ y)$ ，求 $(ξ, η)$ 坐标系下相应的微分方程；
(2): 考虑坐标变换 $(x, y) = e^{u (θ)} (\cos θ, \sin θ)$ ，求 $(u, θ)$ 坐标系下相应的微分方程；
(3): 求解原微分方程。

解 (1) 作坐标变换 $(ξ, η) = (λ x, λ y)$ 可得 $\begin{matrix} (25) & \frac{d η}{d ξ} = \frac{λ d y}{λ d x} = y^{'}, \frac{d^{2} η}{d ξ^{2}} = \frac{d x}{d ξ} \frac{d}{d x} (\frac{d η}{d ξ}) = \frac{y^{″}}{λ} \end{matrix}$ 方便起见，我们仍用 $η^{'}, η^{″}$ 表示 $\frac{d η}{d ξ}, \frac{d^{2} η}{d ξ^{2}}$ ，则原方程可化为 $\begin{matrix} (26) & \frac{η^{″}}{1 + η^{' 2}} + a \frac{ξ η^{'} - η}{ξ^{2} + η^{2}} = 0 \end{matrix}$ 即原方程在原点位似变换下保持不变。

(2) 注意到原方程可化为 $\begin{matrix} (27) & d (\arctan \frac{1}{y^{'}} - a \arctan \frac{y}{x}) = 0 ⟹ \arctan \frac{1}{y^{'}} - a \arctan \frac{y}{x} = C_{1} \end{matrix}$ 计算可得 $\begin{matrix} (28) & \frac{y}{x} = \tan θ, y^{'} = \frac{d y}{d x} = \frac{\frac{d y}{d θ}}{\frac{d x}{d θ}} = \frac{\cos θ + u^{'} (θ) \sin θ}{- \sin θ + u^{'} (θ) \cos θ} = \frac{1 + u^{'} (θ) \tan θ}{u^{'} (θ) - \tan θ} \end{matrix}$ 令 $v (θ) = \arctan u^{'} (θ)$ ，代入可得 $\begin{matrix} (29) & \arctan \frac{\tan v (θ) - \tan θ}{1 + \tan v (θ) \tan θ} - a \arctan \tan θ = C_{1} ⟹ v (θ) - (1 + a) θ = C_{1} \end{matrix}$ 亦即 $\begin{matrix} (30) & \arctan u^{'} (θ) - (1 + a) θ = C_{1} ⟹ \frac{u^{″}}{1 + u^{' 2}} = 1 + a \end{matrix}$

(3) 根据上述过程可得：当 $a \neq - 1$ 时，有 $\begin{matrix} (31) & u^{'} (θ) = \tan ((1 + a) θ + C_{1}) ⟹ u (θ) = - \frac{1}{1 + a} \ln | \cos ((1 + a) θ + C_{1}) | + C_{2} \end{matrix}$ 当 $a = - 1$ 时，有 $\begin{matrix} (32) & v (θ) = {\tilde{C}}_{1} ⟹ u^{'} (θ) = C_{1} ⟹ u (θ) = C_{1} θ + C_{2} \end{matrix}$ 由此得到参数方程形式的通解，转换成隐函数形式可得 $\begin{matrix} (33) & \frac{1}{2} \ln (x^{2} + y^{2}) = u (θ) = {\begin{cases} - \frac{1}{1 + a} \ln | \cos ((1 + a) \arctan \frac{y}{x} + C_{1}) | + C_{2}, & a \neq - 1 \\ C_{1} \arctan \frac{y}{x} + C_{2}, & a = - 1 \end{cases} \end{matrix}$ $◻$

注本题利用了例13.1.5的重要结论：如果一阶微分方程 $\begin{matrix} (34) & \frac{d y}{d x} = f (x, y) \end{matrix}$ 满足 $f$ 是 $k$ 次齐次函数（本题 $k = 1$ ，即在原点位似变换 $(ξ, η) = (λ x, λ y)$ 下保持不变），那么在极坐标变换后，该方程是分离变量的；而指数函数 $ρ (θ) = e^{u (θ)}$ 的选择不仅可以保证半径恒正，还可以将伸缩变换（ $ρ$ 的乘除）转化成平移变换（ $u$ 的加减）。这为我们解决一些特殊的微分方程提供了一种新的思路。

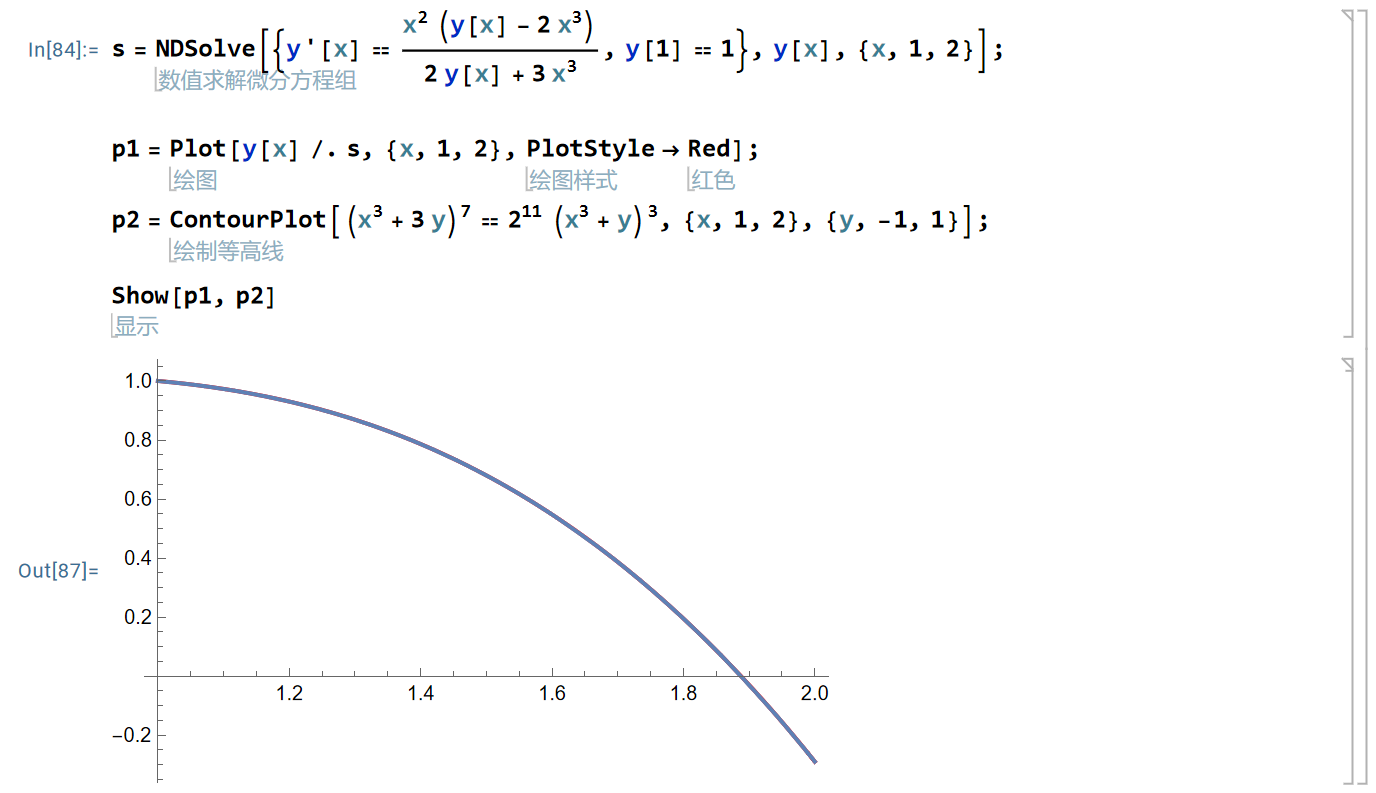
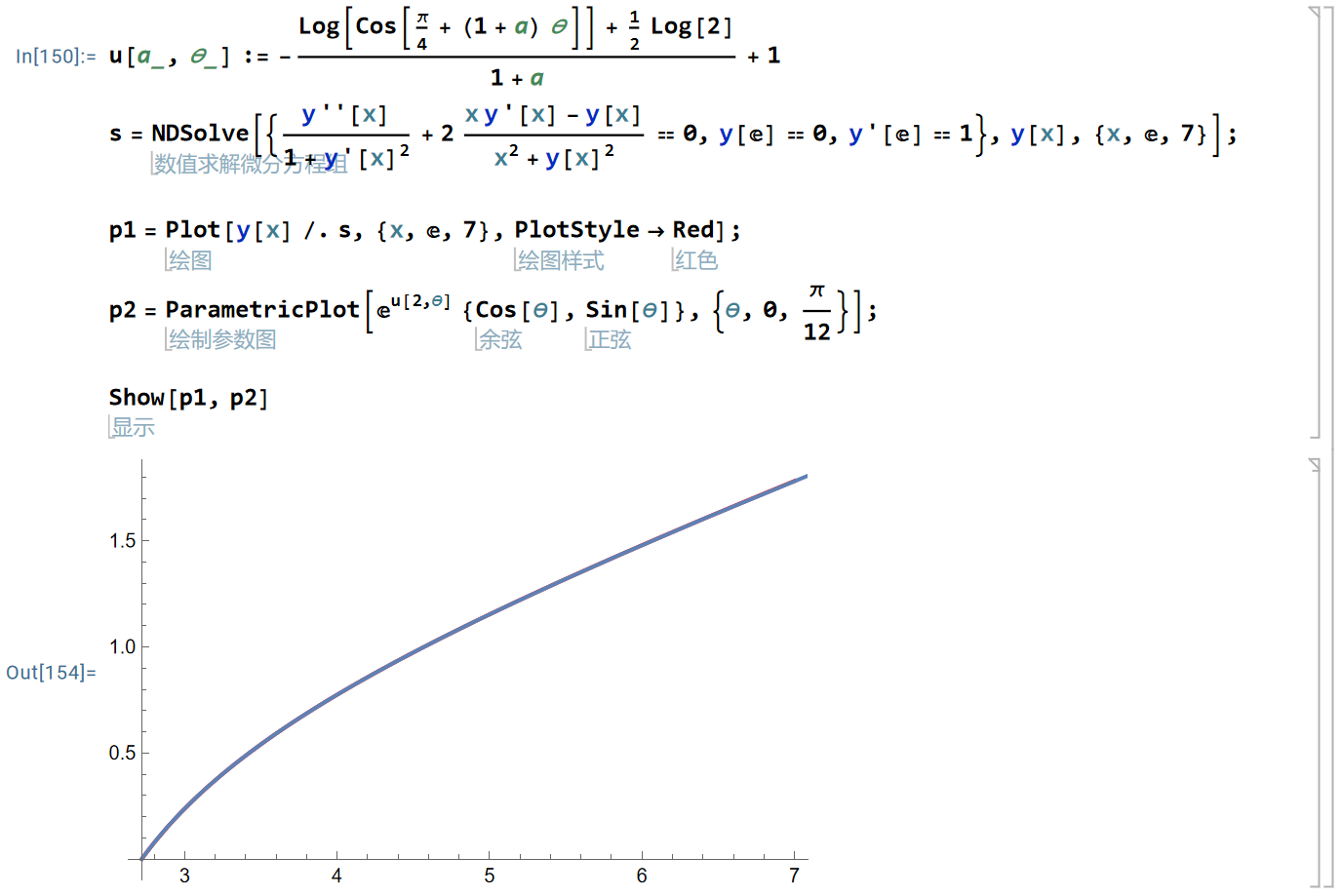
图 13.1.1: 如何在Wolfram Mathematica中数值验证隐函数和参数方程形式的解

例 13.1.8 （习题8.2.11）求解以下微分方程：

(1): $2 x e^{- x^{2}} \sin y d x - e^{- x^{2}} \cos y d y = 0$
(2): $(y e^{x y} + \cos x) d x + x e^{x y} d y = 0$

解 (1) 原方程可化为 $\begin{matrix} (35) & 2 x d x - \cot y d y = 0 ⟹ x^{2} - \ln | \sin y | = \tilde{C} \end{matrix}$ 令 $C = \pm e^{- \tilde{C}}$ 可得原方程的通解为 $\begin{matrix} (36) & y (x) = \arcsin (C e^{x^{2}}) \end{matrix}$

(2) 原方程可化为 $\begin{matrix} (37) & \cos x d x + e^{x y} (y d x + x d y) = d (\sin x + e^{x y}) = 0 ⟹ e^{x y} + \sin x = C \end{matrix}$ 故原方程的通解为 $\begin{matrix} (38) & y = \frac{\ln (C - \sin x)}{x} \end{matrix}$ $◻$

¹此处鸣谢黄添豪、杨鼎两位同学。