习题课讲解

6.3 习题课讲解

6.3.1 基本定理

例 6.3.1 试找“最好的”常数 $A, B$ 使得 $\begin{matrix} (1) & \arctan (1 + x) - \frac{π}{4} \geq \frac{x}{A x + B}, \forall x > 0 \end{matrix}$

解令 $x \to + \infty$ ，则有 $\begin{matrix} (2) & \frac{π}{4} \geq \frac{1}{A} ⟹ A \leq \frac{4}{π} \end{matrix}$ 记 $\begin{matrix} (3) & f (x) := \arctan (1 + x) - \frac{π}{4} - \frac{x}{A x + B} \end{matrix}$ 则有 $\begin{matrix} (4) & f^{'} (0) = \frac{1}{2} - \frac{1}{B} \geq 0 ⟹ B \geq 2 \end{matrix}$ 因此所谓“最好”，就是选择尽可能小的 $A, B$ ，使 $\frac{x}{A x + B}$ 尽可能大。因此，我们可以选择 $A = \frac{4}{π}, B = 2$ ，此时 $\begin{matrix} (5) & f^{'} (x) = - \frac{x [(π^{2} - 8) x - 2 π (4 - π)]}{2 [1 + (x + 1)^{2}] (2 x + π)^{2}} \end{matrix}$ 记 $x^{*} = \frac{2 π (4 - π)}{π^{2} - 8}$ ，则 $f$ 在 $(0, x^{*})$ 上严格增，在 $(x^{*}, + \infty)$ 上严格减，故 $\begin{matrix} (6) & f (x) > min {f (0), f (+ \infty)} = 0, \forall x > 0 \end{matrix}$ 即 $A = \frac{4}{π}, B = 2$ 就是“最好”的。 $◻$

例 6.3.2 求满足 ${(1 + \frac{1}{n})}^{n + α} \leq e \leq {(1 + \frac{1}{n})}^{n + β}$ （ $\forall n \in N^{*}$ ）的参数 $α, β$ 的取值范围。

解采用参数分离法。由 $\ln$ 的单调性可得 $\begin{matrix} (7) & (n + α) \ln (1 + \frac{1}{n}) \leq 1 \leq (n + β) \ln (1 + \frac{1}{n}) \end{matrix}$ 因此 $\begin{matrix} (8) & α \leq f (n) := \frac{1}{\ln (1 + \frac{1}{n})} - n \leq β \end{matrix}$ 考虑定义在 $[1, + \infty)$ 上的连续函数 $f$ ，则 $\begin{matrix} (9) & f^{'} (x) = \frac{1}{x (x + 1) {[\ln (1 + \frac{1}{x})]}^{2}} - 1 \end{matrix}$ 欲证 $f^{'} (x) > 0$ ，只需证 $\begin{matrix} (10) & {[\ln (1 + \frac{1}{x})]}^{2} < \frac{1}{x (x + 1)} \overset{t = x^{- 1}}{=} (1 + t) [\ln (1 + t)]^{2} < t^{2}, \forall t \in (0, 1] \end{matrix}$ 考虑定义在 $[0, 1]$ 上的函数 $g$ $\begin{matrix} (11) & g (t) := t^{2} - (1 + t) [\ln (1 + t)]^{2}, t \in (0, 1] \end{matrix}$ 则 $\begin{matrix} (12) & g^{'} (t) = 2 t - \ln (1 + t) [2 + \ln (1 + t)], g^{″} (t) = \frac{2 (t - \ln (1 + t))}{1 + t} > 0, \forall t \in (0, 1] \end{matrix}$ 因此 $\begin{matrix} (13) & g^{'} (t) > g^{'} (0) = 0, g (t) > g (0) = 0, \forall t \in (0, 1] \end{matrix}$ 因此 $f^{'} (x) > 0$ 在定义域内成立，即 $f$ 在定义域内严格增，故 $\begin{matrix} (14) & α \leq f (1) = \frac{1}{\ln 2} - 1, β \geq f (+ \infty) = \frac{1}{2} \end{matrix}$ 其中由Heine定理可得 $\begin{matrix} (15) & f (+ \infty) = lim_{x \to 0^{+}} [\frac{1}{\ln (1 + x)} - \frac{1}{x}] = lim_{x \to 0^{+}} \frac{\frac{x^{2}}{2} + o (x^{2})}{x^{2} + o (x^{2})} = \frac{1}{2} \end{matrix}$ $◻$

例 6.3.3 证明： $\forall n \in N^{*}$ ， $\begin{matrix} (16) & \frac{1}{2 (n + 1)} < \sum_{k = 1}^{n} \frac{1}{k} - \ln n - γ < \frac{1}{2 n} \end{matrix}$ 其中 $γ := lim_{n \to + \infty} (\sum_{k = 1}^{n} \frac{1}{k} - \ln n)$ 。

证明记 $\begin{matrix} (17) & a_{n} := \sum_{k = 1}^{n} \frac{1}{k} - \ln n - \frac{1}{2 n}, b_{n} := \sum_{k = 1}^{n} \frac{1}{k} - \ln n - \frac{1}{2 (n + 1)} \end{matrix}$ 易见 $lim_{n \to + \infty} a_{n} = lim_{n \to + \infty} b_{n} = γ$ 。为证明 $a_{n} < γ < b_{n}$ ，我们试图证明 $a_{n}$ 严格增、 $b_{n}$ 严格减，即 $\begin{matrix} (18) & \begin{aligned} a_{n + 1} - a_{n} & = \frac{1}{2 n} + \frac{1}{2 (n + 1)} - \ln (1 + \frac{1}{n}) =: f (\frac{1}{n}) \\ b_{n + 1} - b_{n} & = \frac{3}{2 (n + 1)} - \frac{1}{2 (n + 2)} - \ln (1 + \frac{1}{n}) =: g (\frac{1}{n}) \end{aligned} \end{matrix}$ 亦即证明 $\forall x \in (0, 1]$ ， $\begin{matrix} (19) & \begin{aligned} f (x) & = \frac{x}{2} + \frac{x}{2 (1 + x)} - \ln (1 + x) > 0 = f (0) \\ g (x) & = \frac{3 x}{2 (1 + x)} - \frac{x}{2 (1 + 2 x)} - \ln (1 + x) < 0 = g (0) \end{aligned} \end{matrix}$ 求导可得 $\begin{matrix} (20) & f^{'} (x) = \frac{x^{2}}{2 (1 + x)^{2}} > 0, g^{'} (x) = - \frac{x^{2} (5 + 8 x)}{2 (1 + x)^{2} (1 + 2 x)^{2}} < 0, \forall x \in (0, 1] \end{matrix}$ 故 $f, g$ 分别在 $(0, 1]$ 上严格增、严格减，即 $f (x) > 0 > g (x)$ ，故 $a_{n} < γ < b_{n}$ 。 $◻$

6.3.2 不定型极限

例 6.3.4

(1): 设 $f (x)$ 在 $x_{0}$ 处右连续， $lim_{x \to x_{0}^{+}} f^{'} (x) = A \in R$ ，证明 $f$ 在 $x_{0}$ 处有右导数，且 $f_{+}^{'} (x_{0}) = A$ 。
(2): 设 $f (x)$ 在 $x_{0}$ 处连续， $lim_{x \to x_{0}} f^{'} (x) = A \in R$ ，证明 $f$ 在 $x_{0}$ 处有导数，且 $f^{'} (x_{0}) = A$ 。
(3): 设 $f$ 可微，且 $lim_{x \to + \infty} f^{'} (x) = A \in R$ ，若 $y = f (x)$ 在 $x \to + \infty$ 时有渐近线，则渐近线的斜率为 $A$ 。

证明 (1) $\begin{matrix} (21) & f_{+}^{'} (x_{0}) = lim_{x \to x_{0}^{+}} \frac{f (x) - f (x_{0})}{x - x_{0}} \overset{L^{'} H}{=} lim_{x \to x_{0}^{+}} f^{'} (x) = A \end{matrix}$

(2) $\begin{matrix} (22) & f^{'} (x_{0}) = lim_{x \to x_{0}} \frac{f (x) - f (x_{0})}{x - x_{0}} \overset{L^{'} H}{=} lim_{x \to x_{0}} f^{'} (x) = A \end{matrix}$

(3) $\begin{matrix} (23) & lim_{x \to + \infty} \frac{f (x)}{x} \overset{L^{'} H}{=} lim_{x \to + \infty} f^{'} (x) = A \end{matrix}$ $◻$

例 6.3.5 求以下极限

(1): $lim_{x \to 0^{+}} \frac{\ln \cot x}{\ln x}$ 。
(2): $lim_{x \to 0^{+}} x^{α} \ln x$ ，其中 $α > 0$ 。
(3): $lim_{x \to + \infty} \frac{\ln x}{x^{α}}$ ，其中 $α > 0$ 。
(4): $lim_{x \to + \infty} \frac{\frac{π}{2} - \arctan x}{x^{- 1}}$ 。
(5): $lim_{x \to 1} (\frac{x}{x - 1} - \frac{1}{\ln x})$ 。
(6): $lim_{x \to 0} {(\frac{\sin x}{x})}^{x^{- 2}}$ 。
(7): $lim_{x \to 0} \frac{\tan x - \tan \tan x}{\sin x - \sin \sin x}$ 。

解 (1) 分析 $\ln \cot x$ 的主项。注意到 $\begin{matrix} (24) & \ln \cot x = \ln \cos x - \ln \sin x = \ln (1 + o (1)) - \ln [x (1 + o (1))] = - \ln x + o (1) \end{matrix}$ 因此 $\begin{matrix} (25) & \frac{\ln \cot x}{\ln x} = \frac{- \ln x + o (1)}{\ln x} \to - 1, x \to 0^{+} \end{matrix}$

(2) 令 $x^{α} = e^{- t}$ ，则 $t = - α \ln x \to + \infty$ ，注意到 $\begin{matrix} (26) & x^{α} \ln x = - \frac{t}{α e^{t}} \to 0, t \to + \infty \end{matrix}$

(3) 令 $t = x^{α}$ ，则 $x \to + \infty$ 时 $t \to + \infty$ ，注意到 $\begin{matrix} (27) & \frac{\ln x}{x^{α}} = \frac{\ln t}{α t} \to 0, t \to + \infty \end{matrix}$

(4) 令 $t = \frac{π}{2} - \arctan x$ ，则 $\cot t = x$ ，且 $x \to + \infty$ 时 $t \to 0^{+}$ ，注意到 $\begin{matrix} (28) & \frac{\frac{π}{2} - \arctan x}{x^{- 1}} = \frac{t}{\tan t} \to 1, t \to 0^{+} \end{matrix}$

(5) 令 $x = 1 + t$ ，则 $t \to 0$ 时 $x \to 1$ ，注意到 $\begin{matrix} (29) & \frac{x}{x - 1} - \frac{1}{\ln x} = \frac{(1 + t) \ln (1 + t) - t}{t \ln (1 + t)} = \frac{(1 + t) (t - \frac{t^{2}}{2} + o (t^{2})) - t}{t^{2} + o (t^{2})} \to \frac{1}{2}, t \to 0 \end{matrix}$

(6) 考虑其自然对数，注意到 $\begin{matrix} (30) & \frac{1}{x^{2}} \ln \frac{\sin x}{x} = \frac{\ln (1 - \frac{x^{2}}{6} + o (x^{2}))}{x^{2}} = \frac{- \frac{x^{2}}{6} + o (x^{2})}{x^{2}} \to - \frac{1}{6}, x \to 0 \end{matrix}$ 因此原极限为 $e^{- \frac{1}{6}}$ 。

(7) 解法一： $\begin{matrix} (31) & \frac{\tan x - \tan \tan x}{\sin x - \sin \sin x} = \frac{\tan x - (\tan x + \frac{\tan^{3} x}{3} + o (\tan^{3} x))}{\sin x - (\sin x - \frac{\sin^{3} x}{6} + o (\sin^{3} x))} = \frac{- \frac{\tan^{3} x}{3} + o (\tan^{3} x)}{\frac{\sin^{3} x}{6} + o (\sin^{3} x)} \to - 2, x \to 0 \end{matrix}$

解法二：考虑Lagrange中值定理， $\exists ξ \in (x, \tan x)$ 和 $η \in (\sin x, x)$ 使得 $\begin{matrix} (32) & \frac{\tan x - \tan \tan x}{\sin x - \sin \sin x} = \frac{\sec^{2} ξ}{\cos η} \frac{x - \tan x}{x - \sin x} = \frac{\sec^{2} ξ}{\cos η} \frac{x - (x + \frac{x^{3}}{3} + o (x^{3}))}{x - (x - \frac{x^{3}}{6} + o (x^{3}))} \to - 2, x \to 0 \end{matrix}$ $◻$

例 6.3.6 以下解答正确吗？为什么？

(1): 以下极限不存在： $\begin{matrix} (33) & lim_{x \to + \infty} \frac{\sin x^{2}}{\sqrt{x}} = lim_{x \to + \infty} \frac{2 x \cos x^{2}}{\frac{1}{2 \sqrt{x}}} = lim_{x \to + \infty} 4 x^{\frac{3}{2}} \cos x^{2} \end{matrix}$
(2): $\begin{matrix} (34) & lim_{x \to + \infty} \frac{2 x + \sin 2 x}{e^{\sin x} (2 x + \sin 2 x)} = lim_{x \to + \infty} \frac{4 \cos^{2} x}{e^{\sin x} (2 x + \sin 2 x + 4 \cos x) \cos x} = 0 \end{matrix}$

解 (1) 不正确，不能由“导数比值不存在”推出“原极限不存在”。正确的极限为 $0$ 。

(2) 不正确，因为 $g^{'} (x) \neq 0$ 不成立。原极限显然不存在。 $◻$

6.3.3 Taylor展开式（一）

例 6.3.7

(1): 写出 $\sin x, \cos x$ 在 $x = 0$ 处带5阶Peano余项的Taylor展开式。
(2): 写出 $\tan x$ 在 $x = 0$ 处带5阶Peano余项的Taylor展开式。
(3): 设 $f, g \in C^{\infty}$ 满足 $\begin{matrix} (35) & \begin{aligned} f (x) & = x + a_{3} x^{3} + a_{5} x^{5} + a_{7} x^{7} + o (x^{7}), x \to 0 \\ g (x) & = x + b_{3} x^{3} + b_{5} x^{5} + b_{7} x^{7} + o (x^{7}), x \to 0 \end{aligned} \end{matrix}$ 请写出 $f (g (x))$ 在 $x = 0$ 处带7阶Peano余项的Taylor展开式。
(4): 设 $f \in C^{\infty}$ 是可逆的奇函数，且 $\begin{matrix} (36) & f (x) = x + a_{3} x^{3} + a_{5} x^{5} + a_{7} x^{7} + o (x^{7}), x \to 0 \end{matrix}$ 请写出 $f^{- 1}$ 在 $x = 0$ 处带7阶Peano余项的Taylor展开式。
(5): 求极限 $\begin{matrix} (37) & lim_{x \to 0} \frac{\sin \tan x - \tan \sin x}{\arcsin \arctan x - \arctan \arcsin x} \end{matrix}$
(6): 求 $f (x) = \frac{\sin x}{1 + x^{2}}$ 在 $x = 0$ 处带5阶Peano余项的Taylor展开式。

解 (1)(2)(6) $\begin{matrix} (38) & \begin{aligned} \sin x & = x - \frac{x^{3}}{3!} + \frac{x^{5}}{5!} + o (x^{5}) \\ \cos x & = 1 - \frac{x^{2}}{2!} + \frac{x^{4}}{4!} + o (x^{5}) \\ \tan x & = x + \frac{x^{3}}{3} + \frac{2 x^{5}}{15} + o (x^{5}) \\ \frac{\sin x}{1 + x^{2}} & = x - \frac{7 x^{3}}{6} + \frac{47 x^{5}}{40} + o (x^{5}) \end{aligned} \end{matrix}$

(3) 直接展开可得 $\begin{matrix} (39) & \begin{aligned} f (g (x)) & = x + (a_{3} + b_{3}) x^{3} + (a_{5} + 3 a_{3} b_{3} + b_{5}) x^{5} \\ + (a_{7} + 5 a_{5} b_{3} + 3 a_{3} b_{3}^{2} + 3 a_{3} b_{5} + b_{7}) x^{7} + o (x^{7}) \end{aligned} \end{matrix}$

(4) 采用待定系数法可得 $\begin{matrix} (40) & f^{- 1} (x) = x - a_{3} x^{3} + (3 a_{3}^{2} - a_{5}) x^{5} + (- 12 a_{3}^{3} + 8 a_{3} a_{5} - a_{7}) x^{7} + o (x^{7}) \end{matrix}$

(5) 由(3)可知 $\begin{matrix} (41) & f (g (x)) - g (f (x)) = (3 a_{3} b_{3}^{2} - 3 b_{3} a_{3}^{2} - 2 a_{3} b_{5} + 2 a_{5} b_{3}) x^{7} + o (x^{7}) \end{matrix}$ 故 $f \circ g - g \circ f$ 是7阶无穷小。同理可得 $\begin{matrix} (42) & f^{- 1} (g^{- 1} (x)) - g^{- 1} (f^{- 1} (x)) = (3 a_{3} b_{3}^{2} - 3 b_{3} a_{3}^{2} - 2 a_{3} b_{5} + 2 a_{5} b_{3}) x^{7} + o (x^{7}) \end{matrix}$ 即 $f^{- 1} \circ g^{- 1} - g^{- 1} \circ f^{- 1}$ 与 $f \circ g - g \circ f$ 具有相同的7阶无穷小形式，因此 $\begin{matrix} (43) & lim_{x \to 0} \frac{\sin \tan x - \tan \sin x}{\arcsin \arctan x - \arctan \arcsin x} = lim_{x \to 0} \frac{f (g (x)) - g (f (x))}{f^{- 1} (g^{- 1} (x)) - g^{- 1} (f^{- 1} (x))} = 1 \end{matrix}$ $◻$

例 6.3.8 计算以下极限：

(1): $lim_{x \to 0} \frac{e^{x} \sqrt{1 - 2 x} - \cos (\sqrt{2} x)}{\sin^{3} x}$ 。
(2): $lim_{x \to 0} \frac{\cos x - e^{- x^{2} / 2}}{x^{4}}$ 。
(3): $lim_{x \to 1} x^{\frac{1}{1 - x}}$ 。
(4): $lim_{x \to π / 2^{-}} (\tan x)^{π / 2 - x}$ 。
(5): $lim_{x \to 0} [\frac{1}{x} - (\frac{1}{x^{2}} - \frac{1}{x}) \ln (1 + x)]$ 。
(6): $lim_{h \to 0} \frac{f (2 h) + 2 f (- h) - 3 f (0)}{h^{2}}$ ，其中 $f^{″} (0) = 1$ 。
(7): $lim_{x \to 0} \frac{3 x^{2}}{\sqrt{1 + x \sin x} - \sqrt{\cos x}}$ 。
(8): $lim_{n \to + \infty} (\sin \sqrt{n + n^{α}} - \sin \sqrt{n})$ 。
(9): $lim_{n \to + \infty} \sin (2 π \sqrt{n^{2} + α n})$ 。

解 (1) $\begin{matrix} (44) & \begin{aligned} LHS & = \frac{(1 + x + \frac{x^{2}}{2} + \frac{x^{3}}{6} + o (x^{3})) (1 - x - \frac{x^{2}}{2} - \frac{x^{3}}{2} + o (x^{3})) - (1 - x^{2} + o (x^{3}))}{x^{3} (1 + o (1))^{3}} \\ = \frac{- \frac{4}{3} x^{3} + o (x^{3})}{x^{3} + o (x^{3})} \to - \frac{4}{3}, x \to 0 \end{aligned} \end{matrix}$

(2) $\begin{matrix} (45) & LHS = \frac{(1 - \frac{x^{2}}{2} - \frac{x^{4}}{24} + o (x^{4})) - (1 - \frac{x^{2}}{2} + \frac{x^{4}}{8} + o (x^{4}))}{x^{4}} \to - \frac{1}{12}, x \to 0 \end{matrix}$

(3) 令 $t = x - 1 \to 0$ ，则 $\begin{matrix} (46) & x^{\frac{1}{1 - x}} = \exp \frac{\ln (1 + t)}{- t} = \exp (- 1 + o (1)) \to \frac{1}{e}, t \to 0 \end{matrix}$

(4) 令 $t = \frac{π}{2} - x$ ，则 $\begin{matrix} (47) & (\tan x)^{π / 2 - x} = \exp (t \ln \cos t - t \ln \tan t) = \exp (o (1)) \to 1, t \to 0 \end{matrix}$

(5) $\begin{matrix} (48) & LHS = \frac{x - (1 - x) \ln (1 + x)}{x^{2}} = \frac{x - (1 - x) (x - \frac{x^{2}}{2} + o (x^{2}))}{x^{2}} \to \frac{3}{2}, x \to 0 \end{matrix}$

(6) $\begin{matrix} (49) & LHS = \frac{a_{0} + a_{1} (2 h) + \frac{(2 h)^{2}}{2} + o (h^{2}) + 2 a_{0} + 2 a_{1} (- h) + (- h)^{2} + o (h^{2}) - 3 a_{0}}{h^{2}} \to 3, h \to 0 \end{matrix}$

(7) $\begin{matrix} (50) & LHS = \frac{3 x^{2}}{(1 + \frac{1}{2} x^{2} + o (x^{2})) - (1 - \frac{1}{4} x^{2} + o (x^{2}))} \to 4, x \to 0 \end{matrix}$

(8) 当 $α < \frac{1}{2}$ 时，由Lagrange中值定理可得 $\exists ξ \in (n, \sqrt{n + n^{α}})$ $\begin{matrix} (51) & \begin{aligned} LHS & = \cos ξ \cdot [\sqrt{n + n^{α}} - \sqrt{n}] = \cos ξ \cdot \sqrt{n} [{(1 + n^{α - 1})}^{\frac{1}{2}} - 1] \\ = \cos ξ \cdot [\frac{1}{2} n^{α - \frac{1}{2}} + o (n^{α - \frac{1}{2}})] \to 0, n \to + \infty \end{aligned} \end{matrix}$

当 $α = \frac{1}{2}$ ，注意到 $\begin{matrix} (52) & \sqrt{n + \sqrt{n}} - \sqrt{n} = \frac{1}{2} + o (1) ⟹ LHS = \sin (\sqrt{n} + \frac{1}{2}) - \sin \sqrt{n} + o (1), n \to + \infty \end{matrix}$ 由 ${\sin n}_{n \in N}$ 在 $[- 1, 1]$ 上的稠密性知 ${\sin \sqrt{n}}_{n \in N}$ 在 $[- 1, 1]$ 上也是稠密的，故存在子列 ${\sin \sqrt{n_{k}}}_{k \in N}$ 收敛于 $1$ ，此时原数列收敛于 $\cos \frac{1}{2} - 1$ ；也存在子列 ${\sin \sqrt{m_{k}}}_{m \in N}$ 收敛于 $- 1$ ，此时原数列收敛于 $- \cos \frac{1}{2} + 1$ 。因此原极限不存在。

当 $α > \frac{1}{2}$ ，由函数图像（图6.3.1）可知该极限不存在。

(9) 注意到 $\begin{matrix} (53) & 2 π \sqrt{n^{2} + α n} = 2 π n {(1 + \frac{α}{n})}^{\frac{1}{2}} = 2 π n + α π + o (1), n \to + \infty \end{matrix}$ 因此 $\begin{matrix} (54) & \sin (2 π \sqrt{n^{2} + α n}) = \sin (α π + o (1)) \to \sin (α π), n \to + \infty \end{matrix}$ $◻$

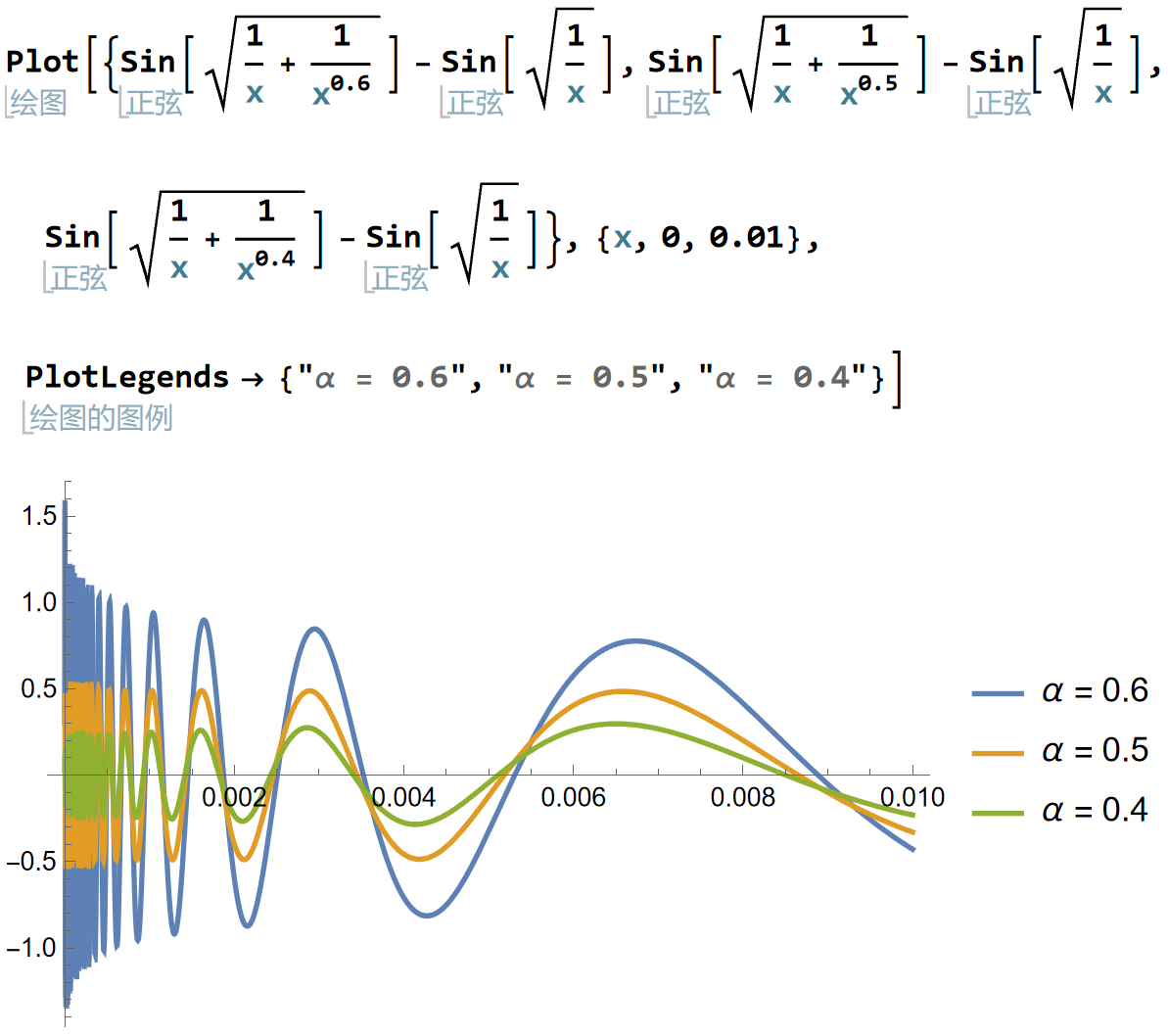
图 6.3.1: $\sin \sqrt{x^{- 1} + x^{- α}} - \sin \sqrt{x^{- 1}}$ 的函数图像

例 6.3.9 设 $f \in C [a, b]$ ，在 $(a, b)$ 上二阶可导，证明 $\exists ξ \in (a, b)$ 使得 $\begin{matrix} (55) & f (b) - 2 f (\frac{a + b}{2}) + f (a) = \frac{(b - a)^{2}}{4} f^{″} (ξ) \end{matrix}$

证明在 $x = \frac{a + b}{2}$ 处作带Lagrange余项的Taylor展开， $\exists ξ_{1} \in (a, \frac{a + b}{2})$ 和 $ξ_{2} \in (\frac{a + b}{2}, b)$ 使得 $\begin{matrix} (56) & \begin{aligned} f (a) & = f (\frac{a + b}{2}) + f^{'} (\frac{a + b}{2}) (a - \frac{a + b}{2}) + \frac{f^{″} (ξ_{1})}{2} {(a - \frac{a + b}{2})}^{2} \\ f (b) & = f (\frac{a + b}{2}) + f^{'} (\frac{a + b}{2}) (b - \frac{a + b}{2}) + \frac{f^{″} (ξ_{2})}{2} {(b - \frac{a + b}{2})}^{2} \end{aligned} \end{matrix}$ 两者相加可得 $\begin{matrix} (57) & f (a) + f (b) = 2 f (\frac{a + b}{2}) + \frac{f^{″} (ξ_{1}) + f^{″} (ξ_{2})}{2} \frac{(b - a)^{2}}{4} \end{matrix}$ 由Darboux定理可知 $\exists ξ \in (ξ_{1}, ξ_{2}) \subseteq (a, b)$ 使得 $f^{″} (ξ) = \frac{f^{″} (ξ_{1}) + f^{″} (ξ_{2})}{2}$ ，因此 $\begin{matrix} (58) & f (b) - 2 f (\frac{a + b}{2}) + f (a) = \frac{(b - a)^{2}}{4} f^{″} (ξ) \end{matrix}$ $◻$

另证构造二次函数 $g (x) = A x^{2} + B x + C$ 满足 $\begin{matrix} (59) & g (a) = f (a), g (\frac{a + b}{2}) = f (\frac{a + b}{2}), g (b) = f (b) \end{matrix}$ 令 $F (x) = f (x) - g (x)$ ，则 $F (b) = F (\frac{a + b}{2}) = F (a) = 0$ ，且待证命题等价于 $\begin{matrix} (60) & [F (b) + g (b)] - 2 [F (\frac{a + b}{2}) + g (\frac{a + b}{2})] + [F (a) + g (a)] = \frac{(b - a)^{2}}{4} [F^{″} (ξ) + g^{″} (ξ)] \end{matrix}$ 注意到 $\begin{matrix} (61) & g (b) - 2 g (\frac{a + b}{2}) + g (a) = \frac{1}{2} (b - a)^{2} A = \frac{(b - a)^{2}}{4} g^{″} (ξ) \end{matrix}$ 故待证命题等价于 $\begin{matrix} (62) & \frac{(b - a)^{2}}{4} F^{″} (ξ) = F (b) - 2 F (\frac{a + b}{2}) + F (a) = 0 ⟺ F^{″} (ξ) = 0 \end{matrix}$ 由于 $F (b) = F (\frac{a + b}{2}) = F (a) = 0$ ，故由Rolle定理可得 $\begin{matrix} (63) & \exists ξ_{1} \in (a, \frac{a + b}{2}), F^{'} (ξ_{1}) = 0; \exists ξ_{2} \in (\frac{a + b}{2}, b), F^{'} (ξ_{2}) = 0 \end{matrix}$ 从而由Rolle定理可得 $\begin{matrix} (64) & \exists ξ \in (ξ_{1}, ξ_{2}) \subseteq (a, b), F^{″} (ξ) = 0 \end{matrix}$ $◻$

例 6.3.10 证明： $\frac{3}{2} < \tan 1 < \frac{π}{2}$ 。

例 6.3.11 设 $f$ 在含 $0$ 的开区间 $I$ 上有连续的 $n + 1$ 阶导数， $f (0) = 0$ ，定义 $\begin{matrix} (65) & F (x) := {\begin{cases} \frac{f (x)}{x}, & x \in I ∖ {0} \\ f^{'} (0), & x = 0 \end{cases} \end{matrix}$ 证明： $F$ 在 $I$ 内有连续的 $n$ 阶导数。

证明设 $I = (a, b)$ ，其中 $- \infty \leq a < 0 < b \leq + \infty$ 。当 $x \neq 0$ 时， $\begin{matrix} (66) & F^{(k)} (x) = \frac{(- 1)^{k} k!}{x^{k + 1}} \sum_{j = 0}^{k} \frac{f^{(j)} (x)}{j!} (- x)^{j} ⟹ F \in C^{k} (a, 0), F \in C^{k} (0, b) \end{matrix}$ 而当 $x \to 0$ 时，在 $x$ 处作带Lagrange余项的Taylor展开可得，存在位于 $0, x$ 之间的 $ξ$ 使得 $\begin{matrix} (67) & f (0) = f (x) + f^{'} (x) (- x) + \dots + \frac{f^{(k)} (x)}{k!} (- x)^{k} + \frac{f^{(k + 1)} (ξ)}{(k + 1)!} (- x)^{k + 1} \end{matrix}$ 故有 $\begin{matrix} (68) & F^{(k)} (x) = \frac{(- 1)^{k} k!}{x^{k + 1}} [f (0) - \frac{f^{(k + 1)} (ξ)}{(k + 1)!} (- x)^{k + 1}] = \frac{f^{(k + 1)} (ξ)}{k + 1} \to \frac{f^{(k + 1)} (0)}{k + 1}, x \to 0 \end{matrix}$ 所以由导数定义和L’Hôpital法则可得 $\begin{matrix} (69) & F^{(k)} (0) = lim_{x \to 0} \frac{F^{(k - 1)} (x) - \frac{f^{(k)} (0)}{k}}{x} \overset{L^{'} H}{=} lim_{x \to 0} F^{(k)} (x) = \frac{f^{(k + 1)} (0)}{k + 1} \end{matrix}$ 归纳可知 $F \in C^{k} (I)$ ，故 $F \in C^{n} (I)$ 。 $◻$

例 6.3.12 设 $f \in C^{\infty}$ ，定义 $\begin{matrix} (70) & F (x) := {\begin{cases} f (e^{- \frac{1}{x^{2}}}), & x \neq 0 \\ f (0), & x = 0 \end{cases} \end{matrix}$ 求 $F$ 在 $x = 0$ 处带 $n$ 阶Peano余项的Taylor展开式。

解归纳可证 $\begin{matrix} (71) & g (x) := {\begin{cases} e^{- \frac{1}{x^{2}}}, & x \neq 0 \\ 0, & x = 0 \end{cases} \end{matrix}$ 为 $C^{\infty}$ 函数，因此 $F = f \circ g \in C^{\infty}$ 。注意到 $\begin{matrix} (72) & | f (g (x)) - f (0) | \leq | f^{'} (ξ) | | g (x) - 0 | \leq M e^{- \frac{1}{x^{2}}} = o (x^{n}), 0 < | x | \leq 1 \end{matrix}$ 因此 $\begin{matrix} (73) & F (x) = f (g (x)) = f (0) + o (x^{n}), x \to 0 \end{matrix}$ 由带Peano余项的Taylor展开式的唯一性可知，这就是 $F$ 在 $x = 0$ 处带 $n$ 阶Peano余项的Taylor展开式。 $◻$

6.3.4 积分因子、微分方程与辅助函数

例 6.3.13 证明： $e^{- λ x}$ 是微分方程 $\begin{matrix} (74) & y^{'} - λ y = 0 \end{matrix}$ 的积分因子。

证明代入验证可得 $\begin{matrix} (75) & {(e^{- λ x} y)}^{'} = e^{- λ x} (y^{'} - λ y) = 0 \end{matrix}$ 从而微分方程的解为 $y = C e^{λ x}$ 。 $◻$

例 6.3.14 求微分方程 $\begin{matrix} (76) & y^{'} + g^{'} (x) y = 0 \end{matrix}$ 的积分因子。

证明代入验证可得 $\begin{matrix} (77) & {(e^{g (x)} y)}^{'} = e^{g (x)} (y^{'} + g^{'} (x) y) = 0 \end{matrix}$ 从而微分方程的解为 $y = C e^{- g (x)}$ 。 $◻$

例 6.3.15 设 $f, g$ 可微， $g$ 有界且 $\begin{matrix} (78) & lim_{x \to + \infty} f (x) = f (0) = 0 \end{matrix}$ 证明： $\exists ξ > 0$ 使得 $\begin{matrix} (79) & f^{'} (ξ) + g^{'} (ξ) f (ξ) = 0 \end{matrix}$

证明令 $F (x) := e^{g (x)} f (x)$ ，则 $F$ 可微，且 $F (0) = F (+ \infty) = 0$ ，由广义Rolle定理可知 $\exists ξ > 0$ 使得 $\begin{matrix} (80) & F^{'} (ξ) = e^{g (ξ)} [f^{'} (ξ) + g^{'} (ξ) f (ξ)] = 0 ⟹ f^{'} (ξ) + g^{'} (ξ) f (ξ) = 0 \end{matrix}$ $◻$

例 6.3.16 设 $f$ 可微，满足 $\begin{matrix} (81) & lim_{x \to + \infty} [f^{'} (x) + f (x)] = a \end{matrix}$ 证明： $\begin{matrix} (82) & lim_{x \to + \infty} f (x) = a, lim_{x \to + \infty} f^{'} (x) = 0 \end{matrix}$

证明令 $F (x) := e^{x} f (x)$ 、 $G (x) := e^{x}$ ，则 $F, G$ 可微且 $\begin{matrix} (83) & lim_{x \to + \infty} f (x) \overset{L^{'} H}{=} lim_{x \to + \infty} \frac{F^{'} (x)}{G^{'} (x)} = lim_{x \to + \infty} [f^{'} (x) + f (x)] = a \end{matrix}$ 因此 $\begin{matrix} (84) & lim_{x \to + \infty} f^{'} (x) = a - lim_{x \to + \infty} f (x) = 0 \end{matrix}$ $◻$