10.2 知识点复习

10.2.1 平面区域的面积

在一元微积分中，我们可以计算以下类型的平面区域的面积：

(1)

设$y_1,y_2\in \mathcal{R}[\alpha ,\beta ]$满足$y_1(x)\le y_2(x)$，则$y_1,y_2$围成的有界区域的面积为$$\begin{array}{}\text{(1)}& S={\int }_{\alpha }^{\beta }(y_2(x)-y_1(x))\mathrm{d}x\end{array}$$

(2)

对于由参数方程确定的简单闭曲线$\gamma :[\alpha ,\beta ]\to {\mathbb{R}}^2$，记$t\mapsto (x(t),y(t))$，其围成的有界区域的面积为$$\begin{array}{}\text{(2)}& \begin{array}{rl}S& ={\int }_{\gamma }x\mathrm{d}y={\int }_{\alpha }^{\beta }x(t)y^{\prime }(t)\mathrm{d}t\\ & =-{\int }_{\gamma }y\mathrm{d}x=-{\int }_{\alpha }^{\beta }y(t)x^{\prime }(t)\mathrm{d}t\\ & =\frac{1}{2}{\int }_{\gamma }(x\mathrm{d}y-y\mathrm{d}x)=\frac{1}{2}{\int }_{\alpha }^{\beta }(x(t)y^{\prime }(t)-y(t)x^{\prime }(t))\mathrm{d}t\\ & =\frac{1}{2}{\int }_{\gamma }\mathit{r}\wedge \mathrm{d}\mathit{r}=\frac{1}{2}{\int }_{\alpha }^{\beta }\mathit{r}(t)\wedge {\mathit{r}}^{\prime }(t)\mathrm{d}t\end{array}\end{array}$$ 上述积分是有向积分，曲线$\gamma$的参数增加方向需要满足区域的自然正向，即：在区域边界按参数增加方向前进时，区域位于左手一侧。

(3)

平面极坐标系下，$$\begin{array}{}\text{(3)}& S=\frac{1}{2}{\int }_{\gamma }{r}^2\mathrm{d}\theta =\frac{1}{2}{\int }_{\alpha }^{\beta }r(t{)}^2{\theta }^{\prime }(t)\mathrm{d}t=\frac{1}{2}{\int }_{{\theta }_1}^{{\theta }_2}r(\theta {)}^2\mathrm{d}\theta \end{array}$$ 在(2)中的第三个公式中代入$x(t)=r(t)\cos \theta (t)$、$y(t)=r(t)\sin \theta (t)$即可得到上式。

10.2.2 曲线的弧长

正则曲线$\mathit{x}(t)\in {\mathcal{C}}^1([\alpha ,\beta ];{\mathbb{R}}^n)$，满足${\mathit{x}}^{\prime }(t)\ne \mathbf{0}$，则其弧长为$$\begin{array}{}\text{(4)}& L={\int }_{\gamma }\mathrm{d}l={\int }_{\alpha }^{\beta }\parallel {\mathit{x}}^{\prime }(t)\parallel \mathrm{d}t\end{array}$$

(1)

在空间直角坐标系下，$$\begin{array}{}\text{(5)}& \mathrm{d}l=\sqrt{\mathrm{d}{x}_1^2+\cdots +\mathrm{d}{x}_n^2}=\sqrt{x_1^{\prime }(t{)}^2+\cdots +x_n^{\prime }(t{)}^2}\mathrm{d}t\end{array}$$

(2)

在平面极坐标系下，我们有$x(t)=r(t)\cos \theta (t)$，$y(t)=r(t)\sin \theta (t)$，则$$\begin{array}{}\text{(6)}& \mathrm{d}l=\sqrt{\mathrm{d}{x}^2+\mathrm{d}{y}^2}=\sqrt{r^{\prime }(t{)}^2+r(t{)}^2{\theta }^{\prime }(t{)}^2}\mathrm{d}t=\sqrt{\mathrm{d}{r}^2+(r\mathrm{d}\theta {)}^2}\end{array}$$

(3)

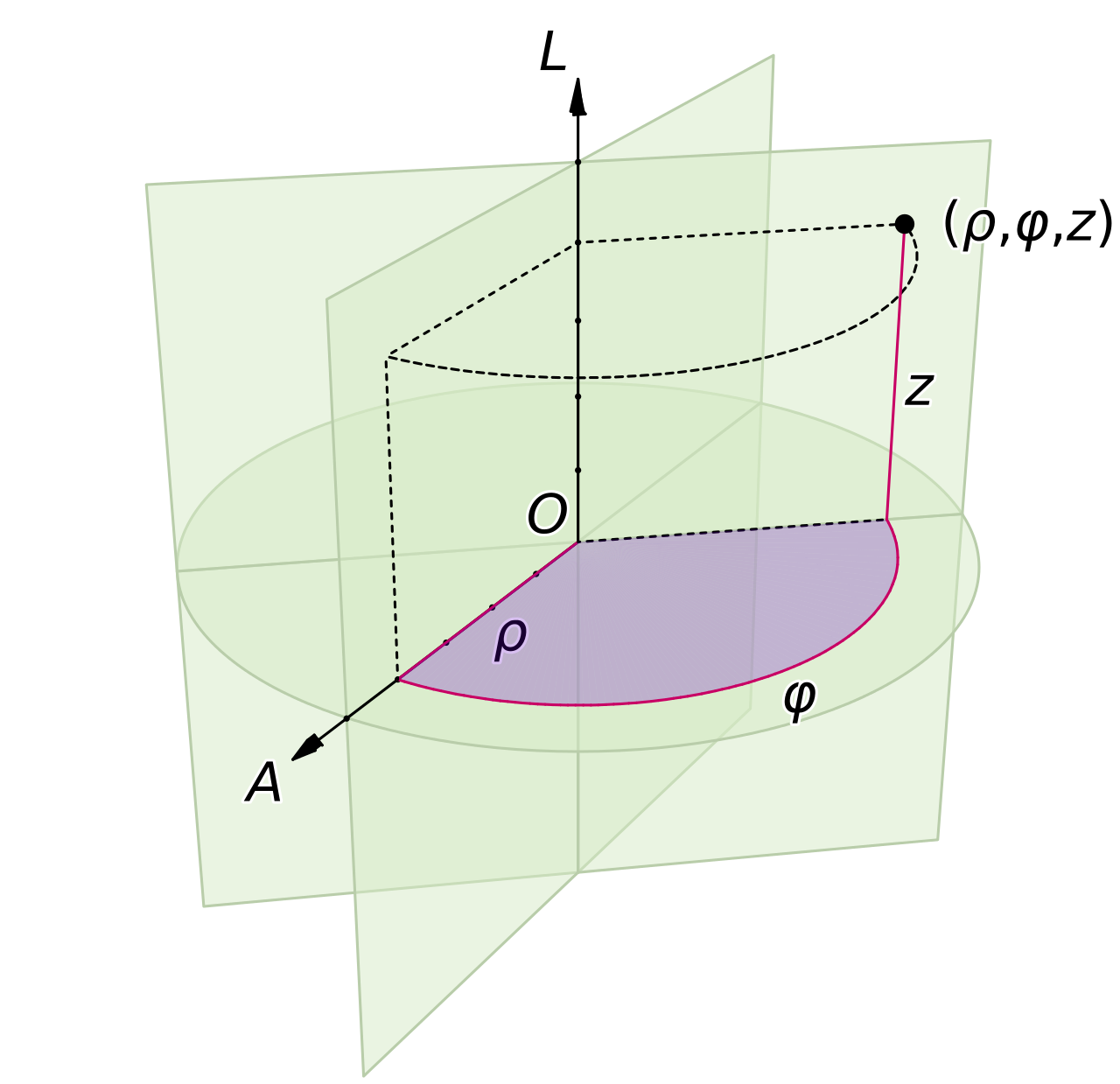
在空间柱坐标系下，我们有$x(t)=r(t)\cos \theta (t)$，$y(t)=r(t)\sin \theta (t)$，$z(t)=z(t)$，则$$\begin{array}{}\text{(7)}& \begin{array}{rl}\mathrm{d}l& =\sqrt{\mathrm{d}{x}^2+\mathrm{d}{y}^2+\mathrm{d}{z}^2}=\sqrt{r^{\prime }(t{)}^2+r(t{)}^2{\theta }^{\prime }(t{)}^2+z^{\prime }(t{)}^2}\mathrm{d}t\\ & =\sqrt{\mathrm{d}{r}^2+(r\mathrm{d}\theta {)}^2+\mathrm{d}{z}^2}\end{array}\end{array}$$

(4)

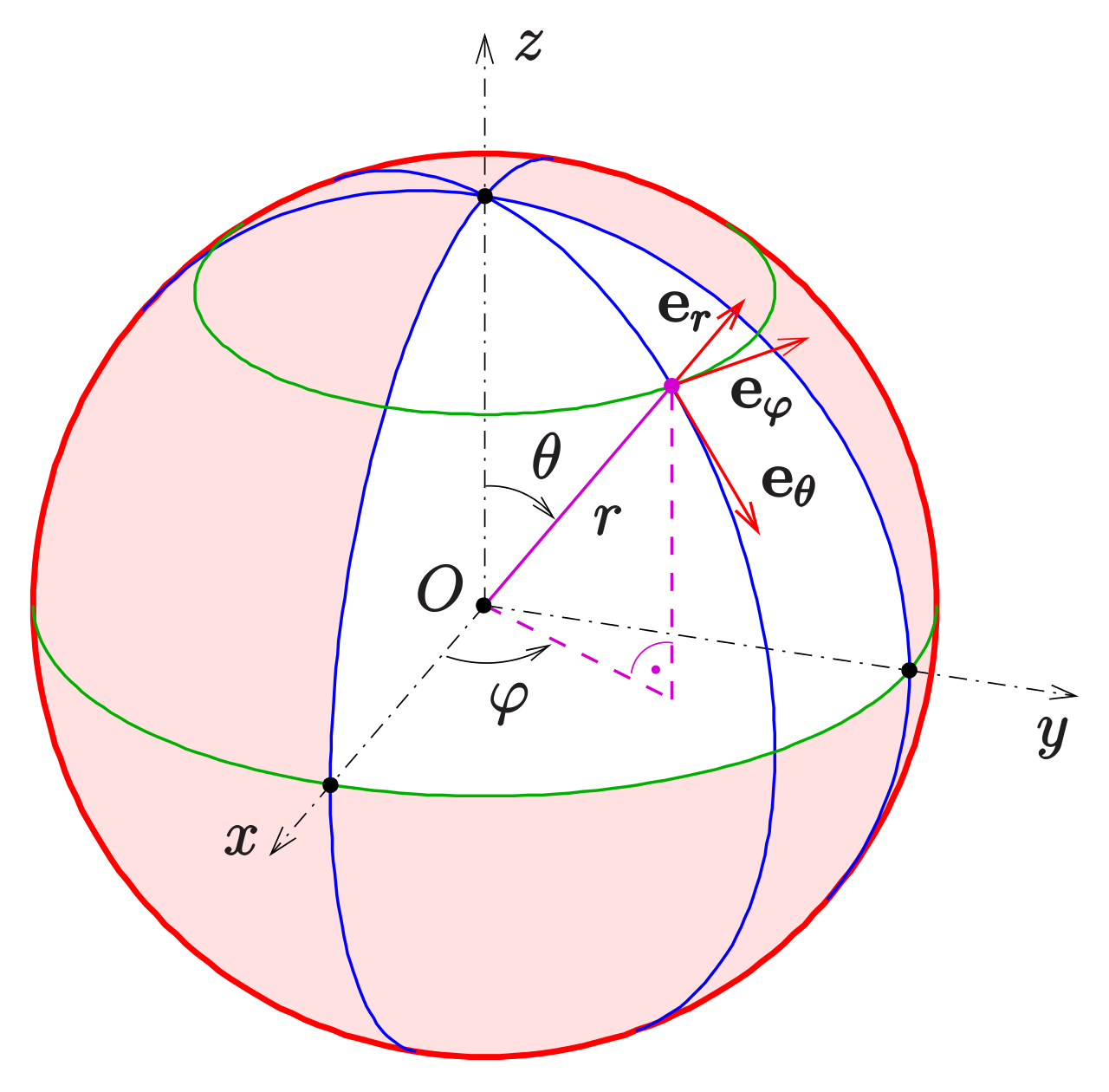
在空间球坐标系下，我们有$x(t)=r(t)\sin \theta (t)\cos \varphi (t)$，$y(t)=r(t)\sin \theta (t)\sin \varphi (t)$，$z(t)=r(t)\cos \theta (t)$，则$$\begin{array}{}\text{(8)}& \begin{array}{rl}\mathrm{d}l& =\sqrt{\mathrm{d}{x}^2+\mathrm{d}{y}^2+\mathrm{d}{z}^2}=\sqrt{r^{\prime }(t{)}^2+r(t{)}^2{\theta }^{\prime }(t{)}^2+r(t{)}^2{\sin }^2\theta (t){\varphi }^{\prime }(t{)}^2}\mathrm{d}t\\ & =\sqrt{\mathrm{d}{r}^2+(r\mathrm{d}\theta {)}^2+(r\sin \theta \mathrm{d}\varphi {)}^2}\end{array}\end{array}$$

以上公式可以借助图像直观地理解，如图10.2.1所示。

(a) 柱坐标系

(b) 球坐标系

10.2.3 曲线的曲率

正则曲线的弧长参数定义为$$\begin{array}{}\text{(9)}& l(t):={\int }_{\alpha }^t\parallel {\mathit{x}}^{\prime }(s)\parallel \mathrm{d}s\end{array}$$ 于是$$\begin{array}{}\text{(10)}& l^{\prime }(t)=\parallel {\mathit{x}}^{\prime }(t)\parallel >0\end{array}$$ 因此$l(t)$有${\mathcal{C}}^1$的反函数$t(l)$，用弧长参数表示的曲线方程$\tilde{\mathit{x}}(l):=\mathit{x}(t(l))$满足$$\begin{array}{}\text{(11)}& {\tilde{\mathit{x}}}^{\prime }(l)=\frac{{\mathit{x}}^{\prime }(t)}{\parallel {\mathit{x}}^{\prime }(t)\parallel },\parallel {\tilde{\mathit{x}}}^{\prime }(l)\parallel =1,⟨{\tilde{\mathit{x}}}^{\prime }(l),{\tilde{\mathit{x}}}^{″}(l)⟩=0\end{array}$$ 这是一个以单位速率运动的曲线，其加速度与速度正交，是曲线的主法向量。曲线的曲率定义为$$\begin{array}{}\text{(12)}& \kappa :=\parallel {\tilde{\mathit{x}}}^{″}(l)\parallel =\frac{\parallel {\mathit{x}}^{\prime }(t)\times {\mathit{x}}^{″}(t)\parallel }{\parallel {\mathit{x}}^{\prime }(t){\parallel }^3}\end{array}$$

10.2.4 旋转体与旋转面

平面封闭曲线$\gamma :[\alpha ,\beta ]\to {\mathbb{R}}^2$位于$x$轴的一侧（包括$x$轴本身），它绕$x$轴旋转一周得到曲面$\mathrm{\Sigma }$和旋转体$\mathrm{\Omega }$，则旋转面（即旋转体侧面）面积为$$\begin{array}{}\text{(13)}& A={\int }_{\gamma }2\pi y\mathrm{d}l=2\pi {\int }_{\alpha }^{\beta }y(t)\sqrt{x^{\prime }(t{)}^2+y^{\prime }(t{)}^2}\mathrm{d}t\end{array}$$ 旋转体体积为$$\begin{array}{}\text{(14)}& V=-{\int }_{\gamma }\pi y^2\mathrm{d}x=-\pi {\int }_{\alpha }^{\beta }y(t{)}^2{x}^{\prime }(t)\mathrm{d}t\end{array}$$ 上述积分中的符号来自于曲线定向。

祖暅原理：沿一个方向把$\mathrm{\Omega }$切割成与$x$轴垂直的一系列薄片，其近似为柱体，设截面面积为$A(x)$、薄体厚度为$\mathrm{d}x$，则薄体体积为$\mathrm{d}V(x)=A(x)\mathrm{d}x$，因此$$\begin{array}{}\text{(15)}& V={\int }_{\alpha }^{\beta }\mathrm{d}V(x)={\int }_{\alpha }^{\beta }A(x)\mathrm{d}x\end{array}$$ 曲面面积的计算是一个很微妙的问题，我们将在多元微积分时有更深入的（但仍是初等的）讨论。

10.2.5 质心与加权平均

设$X\in [\alpha ,\beta ]\subseteq \mathbb{R}$为连续的随机变量，其概率密度函数为$f$，则有$$\begin{array}{}\text{(16)}& {\int }_{\alpha }^{\beta }f(x)\mathrm{d}x=1\end{array}$$ 定义分布函数$F:[\alpha ,\beta ]\to [0,1]$为$$\begin{array}{}\text{(17)}& F(x):={\int }_{\alpha }^{x}f(t)\mathrm{d}t,x\in [\alpha ,\beta ]\end{array}$$ 则$$\begin{array}{}\text{(18)}& \mathrm{d}F(x)=F^{\prime }(x)\mathrm{d}x=f(x)\mathrm{d}x\end{array}$$ 反映了随机变量$X$落在$[x,x+\mathrm{d}x]$的概率。

设$\varphi :[\alpha ,\beta ]\to \mathbb{R}$，则$\varphi (X)$的期望为$$\begin{array}{}\text{(19)}& \mathbb{E}[\varphi (X)]={\int }_{\alpha }^{\beta }\varphi (x)\mathrm{d}F(x)={\int }_{\alpha }^{\beta }\varphi (x)f(x)\mathrm{d}x\end{array}$$ 取$X$为几何体的质量，$\varphi$为恒等映射，则几何体的质心为$$\begin{array}{}\text{(20)}& x_{\mathrm{c}}:=\frac{\int x\mathrm{d}m}{\int \mathrm{d}m}=\frac{{\int }_{\alpha }^{\beta }x\rho (x)\mathrm{d}x}{{\int }_{\alpha }^{\beta }\rho (x)\mathrm{d}x}=:{\int }_{\alpha }^{\beta }xf(x)\mathrm{d}x\end{array}$$ 其中$\rho$为线密度函数（单位长度几何体的质量），权函数（概率密度函数）$f$的定义为线密度函数的归一化，即$$\begin{array}{}\text{(21)}& f(x):=\frac{\rho (x)}{{\int }_{\alpha }^{\beta }\rho (t)\mathrm{d}t}\end{array}$$

以上概念容易推广到高维空间中。