3.2 习题课讲解
3.2.1 单调性与极限
例 3.2.1
设是区间上的单调函数。
-
(1)
-
证明在区间内的间断点都是跳跃间断点。
-
(2)
-
证明至多只有可数个间断点。
-
(3)
-
证明连续当且仅当是区间。
-
(4)
-
若进一步,严格单调,是区间,证明有连续的反函数。
证明
不妨设单调不减。
(1) 对的任何内点,记
易见和均存在,且有。
,都不是的上界,因此且满足。由的单调性可知,。因此,,使得,,即。
同理可知。
若,则在处连续;否则,在处跳跃间断。
(2) 设的间断点集合为,。令满足,满足。由实数的稠密性可知是存在的。
设且满足,则,故,即。故为单射,,即的间断点至多可数。
(3) 我们尝试证明其逆否命题:不连续当且仅当不是区间。
必要性:设在内的某点处间断,由(1)可知在处跳跃间断,故中至多含有一个元素,即不是区间。
充分性:设不是区间,则,使得且。易见。令
显然和、和均存在,且成立以及、。
显然。否则设,,则既是的上界又是的下界,即,与矛盾。
同(1)理可知、。显然,否则设,则,与矛盾。
即为的间断点,即不连续。
(4) 由严格单增知存在,且严格单增。注意到也是区间,由(3)知连续。
注
区间的定义为:称为区间,如果,。
例 3.2.2
设是数列
记
对正整数,记
证明:
-
(1)
-
,极限存在。
-
(2)
-
在上严格增。
-
(3)
-
在每个有理数处间断,在每个无理数处连续。
证明
(1) ,关于单调不减,且
即关于有上界,由单调有界收敛定理知关于的极限存在。
(2) ,不妨设,由于有理数稠密且,故存在使得,因此,有
令,则有
即在上严格增。
(3) ,取,则,满足。故,都有
令,则有
即在处间断。
,,取特定使得,都有
上述第一个“?”可以通过下式满足:
若给定,取
即可。
上述第二个“?”可取。
因此,使得,,即在处连续。
例 3.2.3
设,记
证明对任意,数列收敛于。
问题背景
本题是求解方程的一种迭代方法,称为Newton迭代法。
证明
用数学归纳法可以证明,由AM-GM不等式可得
从而
故单调不增且有下界,从而收敛于。
令递推关系式中的,则有
例 3.2.4
设,记,
求正数的值,使得单调不减;此时证明收敛,并求其极限。
解
(1) 当且仅当,即;由递推公式可知当且仅当,亦即
取充分条件
解得
我们后面还需要验证其必要性。
(2) 此时单调不减,且有上界,故收敛。设极限为,则有
因此
我们验证了(1)中充分条件的必要性。
例 3.2.5
设严格增、连续,证明,存在,且极限值满足。
证明
若,则,,极限显然存在。
若,则由数学归纳法可以证明严格增且有上界,故极限存在。由于连续,故
若,同理可证。
例 3.2.6
在第一次习题课中,我们证明了
因此严格增且有上界,严格减且有下界,故两者极限均存在且相等,记为。记,易见
从而有
利用以上事实,证明数列
收敛。
证明
注意到
故严格减,又
即有下界,故收敛。
例 3.2.7
证明
提示:利用
证明
本题的难点在于如何联系与。先设,则使得(为什么?),因此
即
另一方面,注意到
因此
例 3.2.8
设,,
证明和收敛于同一极限。
证明
由数学归纳法可知。由AM-GM不等式可得
因此
因此从开始,单调减且有下界,单调增且有上界,故两者极限均存在,分别设为。令的递推关系式两边,则
命题背景
上述算法称为算术、几何平均法(Arithmetic-Geometric Mean Method),是迭代计算椭圆积分的最常用的方法。把上述极限值记作初值的函数,定义积分
Gauss“敏锐”地发现
因此
经过变换,积分可转写为第一类完全椭圆积分
由此,我们找到了计算第一类完全椭圆积分的一种方法。
这种方法的收敛速度如何呢?注意到
故这种算法是二阶的,会很快收敛。
例 3.2.9
,定义
证明:
-
(1)
-
当且时,关于严格增。
-
(2)
-
关于有上界。
-
(3)
-
收敛于正数,。
-
(4)
-
设数列有界,。
-
(5)
-
,。
-
(6)
-
在处连续,从而处处连续。
-
(7)
-
关于严格增。
-
(8)
-
的值域为。
解
(1) 由Bernoulli不等式可得
故关于严格增。
(2) 注意到
当时,有
当时,注意到
选择,即即可保证上式成立,此时
故关于有上界。
(3) 由(1)(2)知收敛,设极限为。取,则,且,有
故,且显然有。
(4) 设,。注意到
其中
取即可。
(5) 注意到
故。
(6) 设,注意到
令可得。故,,使得
而,都有,此时,,使得
故处处连续。
(7) 设,对充分大的利用Bernoulli不等式可得
故关于严格增。
(8) 由(6)(7)知连续且严格增,故将区间映射为区间,而
故的值域为。
3.2.2 有界闭区间套
例 3.2.10
设,,,。证明的极限存在,并求它的值。
证明
不妨设,否则可以考虑。用数学归纳法可以证明
于是构成有界闭区间套,从而、存在。令,则有,即。因此。
注意到
因此
即
例 3.2.11
设在开区间上可导,即,极限
存在。证明:若,都有,则在区间上严格增。
证明
记。假设使得且。采用以下方法构造:
- 若,则令,。
- 若,则必然有,令,。
如此可得有界闭区间套,满足
由有界闭区间套定理,存在唯一实数满足,都有。由于区间长度不为,必然存在之一(记为)满足且,因此
由于,令上述不等式两边,得到
这与矛盾。因此在上严格增。
注
构造数列的过程可以形象地用下面这张图表示,相当于不断找(斜率)的最小值点。
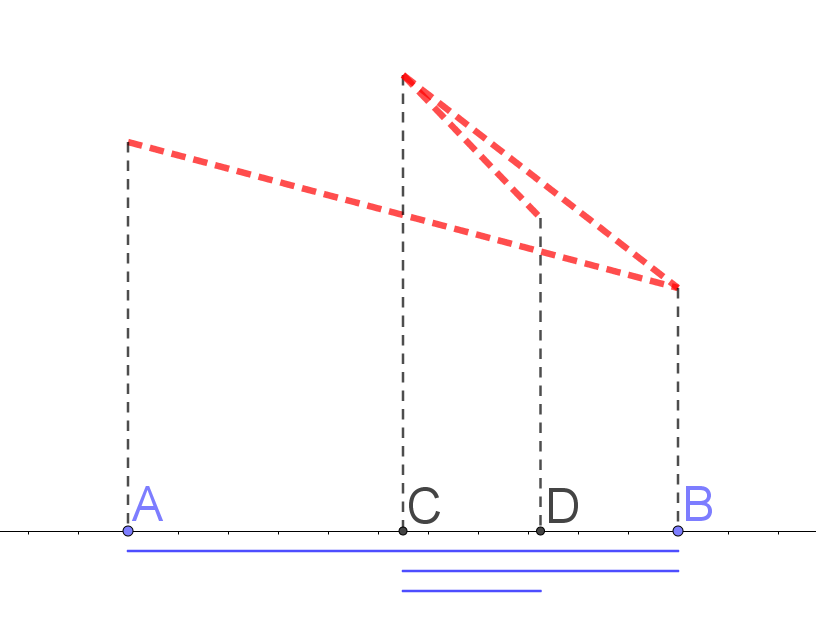
图 3.2.1: 构造数列的过程
3.2.3 Cauchy准则
例 3.2.12
压缩不动点定理。设是闭集,是压缩映射,即存在常数使得,都有。证明:存在唯一的使得,并且,,且
证明
记。若,则命题显然成立。若,则
从而,取特定,使得,有
取
即可。所以是Cauchy数列,于是存在。
在中令可得
易见连续,因此
设均为的不动点,则
即,故不动点唯一。
例 3.2.13
用压缩不动点定理证明例3.2.3。
证明
令
记,由AM-GM不等式可得,且,都有
因此是压缩映射,故有唯一不动点,且,。
例 3.2.14
设,用压缩不动点定理证明例3.2.4。
证明
当时,命题显然成立。故设。令
记,则,都有
故。,都有
因此是压缩映射,故有唯一不动点,且,。
例 3.2.15
设,,。证明存在,并求其值。
证明
令
记,显然,且,都有
并不能保证是压缩映射,故我们考虑
此时
因此是压缩映射,故有唯一不动点。因此
于是,,都有
另解
直接求出的通项。
例 3.2.16
每一种收敛都对应一种Cauchy准则。试写出收敛所对应的Cauchy准则,并给予证明。
证明
当且仅当,,使得,
必要性显然,因为
充分性:任取满足且,则,使得,都有且,因此,即是Cauchy数列,从而存在。令不等式中的可得,因此,
所以。
例 3.2.17
设,,证明:在上连续且所有间断点都是可去间断点当且仅当对于中的任意Cauchy数列,都是Cauchy数列。
证明
必要性:设为中的Cauchy数列,但不是Cauchy数列,则存在,记为。若,则在处连续,此时,这与假设矛盾。若,则是的可去间断点且,此时,这也与假设矛盾。
充分性:设为的聚点,且满足不存在。则,,,使得且,但。取,则,使得且,但,因此是Cauchy数列,但不是Cauchy数列,这与假设矛盾。
因此对的任何聚点,存在。若,则是的可去间断点。若,设,则取、满足,则是Cauchy数列,但不是Cauchy数列,这与假设矛盾。因此在上连续。
例 3.2.18
证明数列
收敛,并证明其极限为。
证明
显然严格增,且有上界
即单调增且有上界,故收敛。
下证其极限为。记,则。注意到
同时
因此。
另证
,取特定,使得,都有
故为Cauchy数列,故收敛。
,取特定,使得,都有
利用Bernoulli不等式可得
因此
因此,即。
例 3.2.19
(指数函数的另一种定义方式,复数指数),定义
证明:
-
(1)
-
关于是Cauchy列,从而存在极限。
-
(2)
-
,对充分大的,有
从而。
-
(3)
-
满足,。
-
(4)
-
对连续。
-
(5)
-
。
![2n2nE2n2n2nE2n2n2n2n2nn++11((zz))EE22nn++11((ww))
0zwE2n+E2n+0−E=zw0−Ezw≤≤≤0zwEn+En+z≤112211((nn(z(wzz++))11[)E+((⋅[⋅2zz⋅⋅nw + +⋅]⋅+)]1ww(w)))](main0x.svg)
图 3.2.2: 证明过程(2)的示意图
证明
(1) 与例3.2.18另解类似。
(2) 本题需要仔细观察等式左右两侧的关系,如图3.2.2所示。此图由个格点构成,点表示求和项。注意到
即为红色区域,为橙色区域,LHS(=两者之差)即为黄色区域,虚线和圆圈表示不包含此点。
不妨设,则图中第一个不等号显然成立,因为双实线上的求和项被计算了两次。对于第二个不等号,我们需要依此证明蓝色和绿色箭头对应的不等式成立,亦即
这两个不等式本质相同,故我们只证明第一个:给定正数,对充分大的和任意,有
只需注意到
由(1)知使得。取即可。
因此,蓝色和绿色箭头对应的不等式成立,从而第二个不等号成立,最终得到的蓝色区域与绿色区域之和即为RHS。当时,采用三角不等式放缩,上述不等号仍然成立,故原不等式成立。
令可得
(3)(4) 与例3.2.9(6)类似。
(5) 见例3.2.18。
例 3.2.20
考虑以下递进的三个问题:
-
(1)
-
设数列满足:,都有。问是否收敛?
-
(2)
-
设数列满足:,都有,其中。问是否收敛?
-
(3)
-
设数列满足:,都有。问是否收敛?
证明
(1)(2) 收敛。只需证明存在使得
为此,计算
故存在使得,都有
从而以及,都有
(1) 是 (2) 的一个特例,即
(3) 可能发散。注意到
令,则满足题设,显然发散。
