1.2 知识点复习
1.2.1 数、运算与数的扩张
数的扩张过程可以用下面这张图来表示。
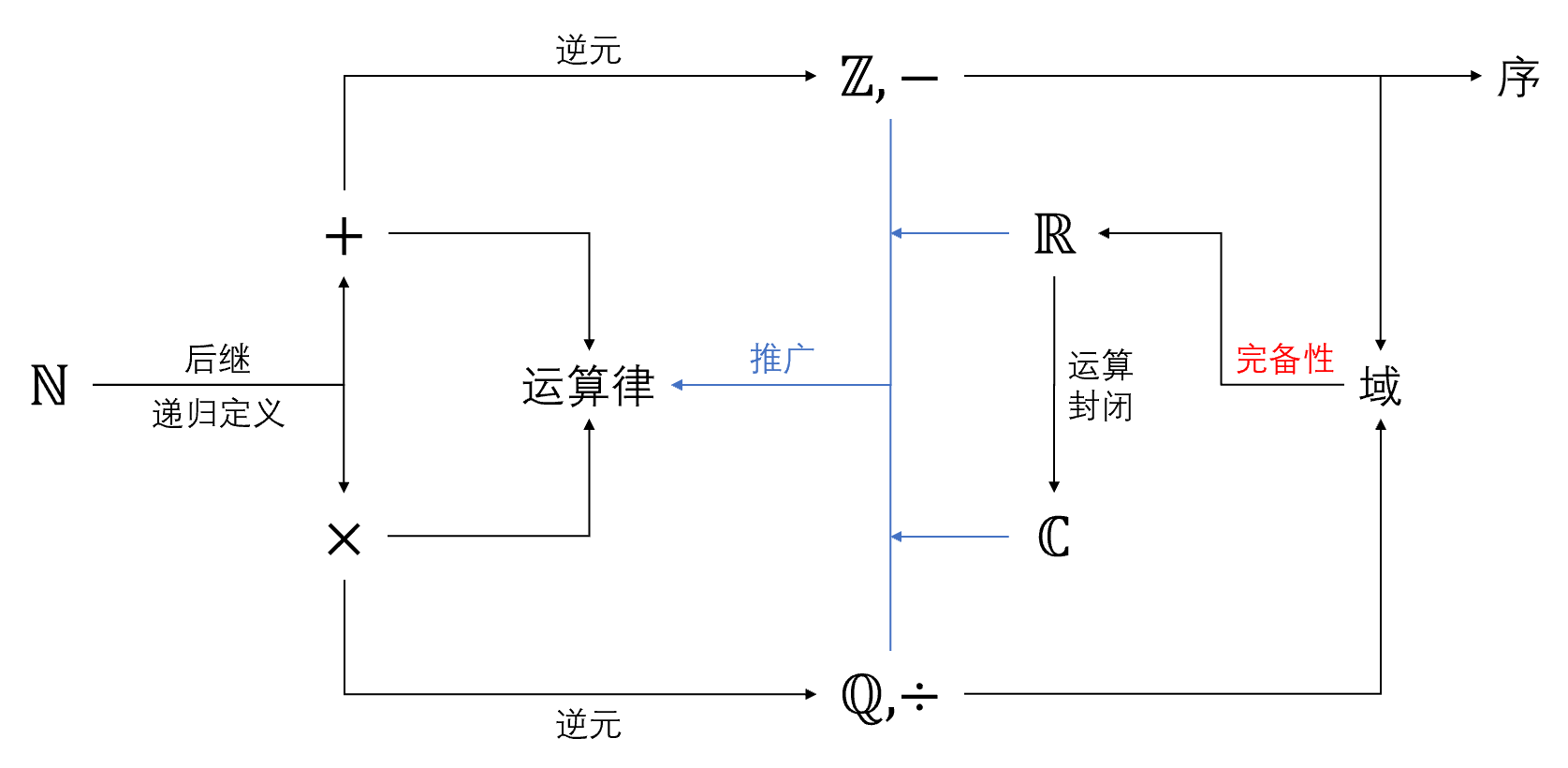
首先,我们通过数学归纳法原理和后继的概念给出了自然数的定义,同时递归定义了加法和乘法。随后,我们利用加法逆元的概念定义了减法和整数,再利用乘法逆元的概念定义了除法和有理数。至此,我们已构建了一个域,即有理数域,它对四则运算封闭。
我们在有理数域中定义了序,并证明了它的三歧性(定理1.3.5和 推论1.3.7),从而给出序域的概念。我们在序域中可以定义绝对值,并给出距离的定义。至此,我们有了度量的手段,为微积分的基本概念——极限作铺垫。
然而,在微积分研究中,仅有有理数域还远远不够。除了老师在课上举的例子以外,我更喜欢下面这种引入方式。在后续的课程中,我们会接触到数列极限的概念,并提出Cauchy收敛准则。这可以算得上微积分中最基本的概念,即:
Cauchy收敛准则是判断数列收敛的好方法,因为它只需要研究数列本身的变化趋势,无需预先“开上帝视角”知道数列的极限值。然而,Cauchy收敛准则成立的条件是完备性,即任何Cauchy点列都能收敛到原空间。这对空间以及空间的度量提出了要求,你能很轻松地在有理数域中构造出这样的数列来:
例 1.2.2
数列
所以仅仅有有理数域是不够的,我们必须要扩张数域。一种扩张的方法就是利用确界11,定义实数为有理数集合的上确界,并给出了
复数最初是在求解一元三次方程的过程中提出的12,不是本课程的重点。
最后,我们在提出自然数时,就提出了基本的运算律,即交换律、结合律和分配律。我们在扩张数的同时,还在不断推广四则运算的定义和运算律的适用范围。推广是引入新数学概念的常见思路,读者可在学习中不断体会这一点。
读者可以按以上思路厘清这一章的逻辑,并复习以下知识点:
- (1)
-
自然数集、数学归纳法原理、后继、加法、乘法、结合律、交换律、分配律。
- (2)
-
整数集、减法、加法单位元、加法逆元。
- (3)
-
有理数集、除法、乘法单位元、乘法逆元、序、距离、域。
- (4)
-
实数、实数的序、阿基米德性质。
1.2.2 确界
重要概念回顾 有(上、下)界、上(下)界、最大(小)值、上(下)确界。
- (1)
-
确界公理的一个重要应用是(非空有上界的)集合的上界集合一定有最小值。
- (2)
-
确界有多种等价表述,以集合