[prev ] [up ]
7.3 7.3.1 菲赫金哥尔茨《微积分学教程》第一卷中有一小节插值法讲了这个内容,这本来是数值分析里讲插值逼近误差分析的内容,但被讲数学分析的人用来构造各种吓人的中值问题。
例 7.3.1
(刘/章/闫 · 习题4.1.13)设函数 f , g , h 在 [ a , b ] 上连续、在 ( a , b ) 内可导,证明: ∃ ξ ∈ ( a , b ) 使得 (1) | f ( a ) g ( a ) h ( a ) f ( b ) g ( b ) h ( b ) f ′ ( ξ ) g ′ ( ξ ) h ′ ( ξ ) | = 0
(2) F ( x ) := | f ( a ) g ( a ) h ( a ) f ( b ) g ( b ) h ( b ) f ( x ) g ( x ) h ( x ) | ⟹ F ( a ) = F ( b ) = 0 ∃ ξ ∈ ( a , b ) F ′ ( ξ ) = 0 (3) F ′ ( ξ ) = | f ( a ) g ( a ) h ( a ) f ( b ) g ( b ) h ( b ) f ′ ( ξ ) g ′ ( ξ ) h ′ ( ξ ) | = 0 ◻
例 7.3.2
(刘/章/闫 · 习题4.1.14)设 f 在 [ a , b ] 上一阶可导,在 ( a , b ) 内二阶可导,且 f ( a ) = f ( b ) = 0 、 f + ′ ( a ) f − ′ ( b ) > 0 ,证明:
(1)
∃ ξ ∈ ( a , b ) ,使得 f ″ ( ξ ) + 2 f ′ ( ξ ) + f ( ξ ) = 0 。
(2)
∃ θ ∈ ( a , b ) ,使得 f ″ ( θ ) − 2 f ′ ( θ ) + f ( θ ) = 0 。
(3)
∃ η ∈ ( a , b ) ,使得 f ″ ( η ) = f ′ ( η ) 。
(4)
∃ ζ ∈ ( a , b ) ,使得 f ″ ( ζ ) = f ( ζ ) 。
我们先证明如下引理:
引理 7.3.3
设 f 在 [ a , b ] 上一阶可导,在 ( a , b ) 内二阶可导,且 f ( a ) = f ( b ) = 0 、 f + ′ ( a ) f − ′ ( b ) > 0 ,则 ∃ ξ 1 , ξ 2 , ξ ∈ ( a , b ) ,使得 f ′ ( ξ 1 ) = f ′ ( ξ 2 ) = f ″ ( ξ ) = 0 。
f + ′ ( a ) > 0 − f ε = 1 2 f + ′ ( a ) ∃ δ ∈ ( 0 , b − a 2 ) (4) 0 < x − a < δ ⟹ − ε < f ( x ) − f ( a ) x − a − f + ′ ( a ) < ε ⟹ f ( x ) > 1 2 f + ′ ( a ) ( x − a ) > 0 ∃ x 1 ∈ ( a , a + δ ) ⊆ ( a , a + b 2 ) f ( x 1 ) = 0 ∃ x 2 ∈ ( b − δ , b ) ⊆ ( a + b 2 , b ) f ( x 2 ) = 0 ∃ x 0 ∈ ( x 1 , x 2 ) f ( x 0 ) = 0
反复应用Rolle定理可得:∃ ξ 1 ∈ ( a , x 0 ) f ′ ( ξ 1 ) = 0 ∃ ξ 2 ∈ ( x 0 , b ) f ′ ( ξ 2 ) = 0 ∃ ξ ∈ ( ξ 1 , ξ 2 ) ⊆ ( a , b ) f ″ ( ξ ) = 0
F ( x ) = e x f ( x ) F ( a ) = F ( b ) = 0 (5) F + ′ ( a ) F − ′ ( b ) = e a + b f + ′ ( a ) f − ′ ( b ) > 0 ∃ ξ ∈ ( a , b ) F ″ ( ξ ) = 0 (6) f ″ ( ξ ) + 2 f ′ ( ξ ) + f ( ξ ) = 0
(2) 令G ( x ) = e − x f ( x ) G ( a ) = G ( b ) = 0 (7) G + ′ ( a ) G − ′ ( b ) = e − a − b f + ′ ( a ) f − ′ ( b ) > 0 ∃ θ ∈ ( a , b ) G ″ ( θ ) = 0 (8) f ″ ( θ ) − 2 f ′ ( θ ) + f ( θ ) = 0
(3) 令H ( x ) = e − x f ′ ( x ) f ′ ( ξ 1 ) = f ′ ( ξ 2 ) = 0 H ( ξ 1 ) = H ( ξ 2 ) = 0 ∃ η ∈ ( ξ 1 , ξ 2 ) ⊆ ( a , b ) H ′ ( η ) = 0 (9) f ″ ( η ) = f ′ ( η )
(4) 令I ( x ) = e − x ( f ( x ) + f ′ ( x ) ) ∃ ζ 1 , ζ 2 ∈ ( a , b ) F ′ ( ζ 1 ) = F ′ ( ζ 2 ) = 0 I ( ζ 1 ) = I ( ζ 2 ) = 0 ∃ ζ ∈ ( ζ 1 , ζ 2 ) ⊆ ( a , b ) I ′ ( ζ ) = 0 (10) f ″ ( ζ ) = f ( ζ ) ◻
例 7.3.4
(刘/章/闫 · 习题4.3.9)设函数 f ∈ C 3 [ 0 , 1 ] ,且 f ( 0 ) = f ′ ( 1 2 ) = 0 、 f ( 1 ) = 1 2 。证明: ∃ ξ ∈ ( 0 , 1 ) ,使得 f ‴ ( ξ ) = 12 。
f 0 = f ( 1 2 ) g ( x ) = a 3 x 3 + a 2 x 2 + a 1 x + a 0 (11) g ( 0 ) = g ′ ( 1 2 ) = 0 , g ( 1 2 ) = f 0 , g ( 1 ) = 1 2 ⟹ g ( x ) = 2 x 3 − 2 ( 1 + 2 f 0 ) x 2 + 1 + 8 f 0 2 x F ( x ) = f ( x ) − g ( x ) F ( 0 ) = F ( 1 2 ) = F ( 1 ) = F ′ ( 1 2 ) = 0
∃ ξ 1 ∈ ( 0 , 1 2 ) F ′ ( ξ 1 ) = 0 ∃ ξ 2 ∈ ( 1 2 , 1 ) F ′ ( ξ 2 ) = 0 ∃ η 1 ∈ ( ξ 1 , 1 2 ) F ″ ( η 1 ) = 0 ∃ η 2 ∈ ( 1 2 , ξ 2 ) F ″ ( η 2 ) = 0 ∃ ξ ∈ ( η 1 , η 2 ) ⊆ ( a , b ) F ‴ ( ξ ) = 0 f ‴ ( ξ ) = g ‴ ( ξ ) = 12
◻
例 7.3.5
(刘/章/闫 · 习题4.3.11)设 h > 0 ,函数 f ∈ C 1 [ x 0 − h , x 0 + h ] 。证明: ∃ θ ∈ ( 0 , 1 ) ,使得 (12) f ( x 0 + h ) − f ( x 0 − h ) = [ f ′ ( x 0 + θ h ) + f ′ ( x 0 − θ h ) ] h
F : [ 0 , 1 ] → R F ( x ) = f ( x 0 + x h ) − f ( x 0 − x h ) ∃ θ ∈ ( 0 , 1 ) (13) f ( x 0 + h ) − f ( x 0 − h ) = F ( 1 ) − F ( 0 ) = F ′ ( θ ) = [ f ′ ( x 0 + θ h ) + f ′ ( x 0 − θ h ) ] h ◻
例 7.3.6
(刘/章/闫 · 习题4.3.12)设函数 f ∈ C 1 [ a , b ] ,在 ( a , b ) 内二阶可导,且 f ′ ( a ) = f ′ ( b ) = 0 。证明: ∃ ξ ∈ ( a , b ) ,使得 (14) | f ″ ( ξ ) | ≥ 4 ( b − a ) 2 | f ( b ) − f ( a ) |
(15) f ( a + b 2 ) = f ( a ) − f ′ ( a ) b − a 2 + f ″ ( ξ 1 ) 2 ( b − a 2 ) 2 = f ( a ) + f ″ ( ξ 1 ) 8 ( b − a ) 2 = f ( b ) + f ′ ( b ) b − a 2 + f ″ ( ξ 2 ) 2 ( b − a 2 ) 2 = f ( b ) + f ″ ( ξ 2 ) 8 ( b − a ) 2 (16) f ( b ) − f ( a ) = ( b − a ) 2 8 [ f ″ ( ξ 1 ) − f ″ ( ξ 2 ) ] ξ ∈ { ξ 1 , ξ 2 } | f ″ ( ξ ) | = max { | f ″ ( ξ 1 ) | , | f ″ ( ξ 2 ) | } (17) | f ( b ) − f ( a ) | ≤ ( b − a ) 2 8 [ | f ″ ( ξ 1 ) | + | f ″ ( ξ 2 ) | ] ≤ ( b − a ) 2 4 | f ″ ( ξ ) | ◻
例 7.3.7
(楼红卫 · 例6.5.4)设函数 f ∈ C 1 [ a , b ] ,在 ( a , b ) 内三阶可导。证明: ∃ ξ ∈ ( a , b ) ,使得 (18) f ( b ) = f ( a ) + 1 2 ( b − a ) ( f ′ ( a ) + f ′ ( b ) ) − 1 12 ( b − a ) 3 f ‴ ( ξ )
g ( x ) = a 3 x 3 + a 2 x 2 + a 1 x + a 0 (19) g ( a ) = f ( a ) , g ( b ) = f ( b ) , g ′ ( a ) = f ′ ( a ) , g ′ ( b ) = f ′ ( b ) g (20) | g ( x ) 1 x x 2 x 3 f ( a ) 1 a a 2 a 3 f ( b ) 1 b b 2 b 3 f ′ ( a ) 0 1 2 a 3 a 2 f ′ ( b ) 0 1 2 b 3 b 2 | = 0 ⟹ | g ‴ ( x ) 0 0 0 6 f ( a ) 1 a a 2 a 3 f ( b ) 1 b b 2 b 3 f ′ ( a ) 0 1 2 a 3 a 2 f ′ ( b ) 0 1 2 b 3 b 2 | = 0 (21) g ‴ ( x ) = − 12 ( b − a ) 3 [ f ( b ) − f ( a ) ] + 6 ( b − a ) 2 [ f ′ ( a ) + f ′ ( b ) ] F ( x ) = f ( x ) − g ( x ) F ( a ) = F ( b ) = F ′ ( a ) = F ′ ( b ) = 0
∃ η ∈ ( a , b ) F ′ ( η ) = 0 ∃ ξ 1 ∈ ( a , η ) F ″ ( ξ 1 ) = 0 ∃ ξ 2 ∈ ( η , b ) F ″ ( ξ 2 ) = 0 ∃ ξ ∈ ( ξ 1 , ξ 2 ) ⊆ ( a , b ) F ‴ ( ξ ) = 0 (22) f ( b ) = f ( a ) + 1 2 ( b − a ) ( f ′ ( a ) + f ′ ( b ) ) − 1 12 ( b − a ) 3 f ‴ ( ξ )
◻
7.3.2
例 7.3.8
阿基米德提出用圆内接正多边形的周长逼近圆的周长,从而计算圆周率的近似值。荷兰的Ludolph van Ceulen用一生的时间计算了 2 62 边形,得到圆周率的 35 位小数。由初等的平面几何知识可得:半径为 1 的圆内接正 3 ⋅ 2 n 边形的边长 a n 和周长 L n 满足递推关系: (23) a n + 1 = 2 − 2 1 − ( a n 2 ) 2 = a n 1 2 + 4 − a n 2 L n + 1 = 3 ⋅ 2 n + 1 a n + 1 = L n 2 1 + 1 − ( L n 3 ⋅ 2 n ) 2 然而,这个公式收敛很慢。试确定常数 λ ,使得数列 { ( 1 − λ ) L n + λ L n + 1 } 具有最快的收敛速度。
(24) L n = 3 ⋅ 2 n + 1 sin 2 π 3 ⋅ 2 n + 1 = 3 ⋅ 2 n + 1 [ 2 π 3 ⋅ 2 n + 1 − 1 6 ( 2 π 3 ⋅ 2 n + 1 ) 3 + O ( 1 2 5 n ) ] = 2 π − π 3 27 ⋅ 2 2 n + O ( 1 2 4 n ) (25) ( 1 − λ ) L n + λ L n + 1 = 2 π − ( 4 − 3 λ ) π 3 27 ⋅ 2 2 n + 2 + O ( 1 2 4 n ) λ = 4 3 (26) L ~ n = − 1 3 L n + 4 3 L n + 1 = 2 π + O ( 1 2 4 n ) ◻
例 7.3.9
(1)
证明: ∀ x ∈ [ − 1 , 1 ] , (27) arctan x = x − x 3 3 + x 5 5 − ⋯ + ( − 1 ) n x 2 n + 1 2 n + 1 + ⋯
(2)
利用 arctan 1 2 + arctan 1 3 = π 4 ,求 π 的近似值。
(28) ( arctan x ) ′ = 1 1 + x 2 = 1 − x 2 + x 4 − ⋯ + ( − 1 ) n x 2 n + o ( x 2 n ) ∃ ξ ∈ ( − 1 , 1 ) (29) arctan x = x − x 3 3 + x 5 5 − ⋯ + ( − 1 ) n x 2 n + 1 2 n + 1 + arctan ( 2 n + 2 ) ( ξ ) ( 2 n + 2 ) ! x 2 n + 2 (30) ( arctan x ) ′ = 1 1 + x 2 = 1 2 i ( 1 x + i − 1 x − i ) (31) arctan ( n + 1 ) ( x ) = ( − 1 ) n n ! 2 i ( 1 ( x − i ) n + 1 − 1 ( x + i ) n + 1 ) (32) | arctan ( n + 1 ) ( x ) ( n + 1 ) ! | ≤ 2 2 ( n + 1 ) max { 1 | x − i | n + 1 , 1 | x + i | n + 1 } ≤ 1 n + 1 (33) | arctan ( 2 n + 2 ) ( ξ ) ( 2 n + 2 ) ! x 2 n + 2 | ≤ | x | 2 n + 2 2 n + 2 ≤ 1 2 n + 2 → 0 , n → + ∞ , ξ ∈ ( − 1 , 1 ) (34) arctan x = x − x 3 3 + x 5 5 − ⋯ + ( − 1 ) n x 2 n + 1 2 n + 1 + ⋯
(2) 由题可得(35) π 4 = arctan 1 2 + arctan 1 3 = ∑ n = 1 + ∞ ( − 1 ) n − 1 2 n − 1 ( 1 2 2 n − 1 + 1 3 2 n − 1 ) 22 π 3.141592653589790 14 ◻
7.3.3
例 7.3.10
证明: ∀ x 1 , ⋯ , x n ∈ R + ,都有 (36) x 1 x 1 ⋯ x n x n ≥ ( x 1 + ⋯ + x n n ) x 1 + ⋯ + x n
f ( x ) := x ln x f ″ ( x ) = 1 x > 0 ∀ x > 0 f (37) f ( x 1 + ⋯ + x n n ) ≤ f ( x 1 ) + ⋯ + f ( x n ) n (38) x 1 + ⋯ + x n n ln x 1 + ⋯ + x n n ≤ x 1 ln x 1 + ⋯ + x n ln x n n exp ◻
7.3.4
例 7.3.11
设 f 在区间 [ a , + ∞ ) 上是凸函数, y = k x + b 是 y = f ( x ) 在 x → + ∞ 时的一条渐近线。证明:
(1)
若 f 可微,则 lim x → + ∞ f ′ ( x ) = k 。
(2)
若 f 可微,则 f ( x ) ≥ k x + b , ∀ x ≥ a 。
(3)
若 f 严格凸,则 f ( x ) > k x + b , ∀ x > a 。
f f ′ lim x → + ∞ f ′ ( x ) = A ∈ R ∪ { + ∞ } A ∈ R f ′ (39) k = lim x → + ∞ f ( x ) x = lim x → + ∞ f ′ ( x ) = A
(2) 考虑函数g ( x ) := f ( x ) − k x − b g ′ ( x ) = f ′ ( x ) − k g g ′ g ′ ( x ) ≤ g ′ ( + ∞ ) = 0 g g ( x ) ≥ g ( + ∞ ) = 0 f ( x ) ≥ k x + b
(3) 考虑函数g ( x ) := f ( x ) − k x − b g g ( + ∞ ) = 0
假设∃ x 1 ≥ a g ( x 1 ) ≤ 0 x 2 > x 1 g ( x 2 ) > g ( x 1 ) ∀ x > x 2 (40) g ( x ) − g ( x 2 ) x − x 2 > g ( x 2 ) − g ( x 1 ) x 2 − x 1 (41) g ( x ) > g ( x 2 ) + g ( x 2 ) − g ( x 1 ) x 2 − x 1 ( x − x 2 ) → + ∞ , x → + ∞ g ( + ∞ ) = 0 ∀ x > x 1 g ( x ) ≤ g ( x 1 ) 0 = g ( + ∞ ) ≤ g ( x 1 ) g ( x 1 ) = 0
∀ x > x 1 g ( x ) ≤ g ( x 1 ) = 0 g ( x ) = 0 g ( x ) ≡ 0 ∀ x ≥ x 1 g ∀ x > a g ( x ) > 0 f ( x ) > k x + b ◻
例 7.3.12
讨论函数 f ( x ) = 2 x 2 x + 1 的凹凸性和渐近线。
(42) f ′ ( x ) = 2 ( x − 1 ) + 2 x + 1 , f ″ ( x ) = 4 ( x + 1 ) 3 x < − 1 f ″ ( x ) < 0 f x > − 1 f ″ ( x ) > 0 f
注意到lim x → − 1 f ( x ) = ∞ x = − 1 y = f ( x ) f ( x ) = 2 x − 2 + o ( 1 ) x → ∞ y = 2 x − 2 y = f ( x ) x → ∞ x < − 1 y = f ( x ) x > − 1 y = f ( x ) ◻
例 7.3.13
讨论平面曲线 x 3 + y 3 = 3 x y 的渐近线和曲线的位置关系。
t = y x (43) x ( t ) = 3 t t 3 + 1 , y ( t ) = 3 t 2 t 3 + 1 , t ∈ R ∖ { − 1 } t → − 1 x ( t ) → ∞ (44) y ( t ) x ( t ) = t → − 1 , y ( t ) + x ( t ) t = 3 t ( 1 + t ) 1 + t 3 → − 1 , t → − 1 y = − x − 1 (45) y ( t ) + x ( t ) + 1 = t 3 + 3 t 2 + 3 t + 1 1 + t 3 = ( t + 1 ) 2 1 − t + t 2 > 0 ◻
7.3.5
例 7.3.14
计算极限:
(1)
lim x → + ∞ x ln x ( ln x ) x 。
(2)
lim n → + ∞ ( n + 9 n 2 − n 3 3 ) 。
(3)
lim x → 0 sin x − arctan x tan x − arcsin x 。
(4)
lim n → + ∞ 1 ln n ( 1 + 1 3 + 1 5 + ⋯ + 1 2 n − 1 ) 。
t = ln x → + ∞ (46) x ln x ( ln x ) x = exp [ ( ln x ) 2 − x ln ln x ] = exp [ t 2 − e t ln t ] ≤ exp [ t 2 − e t ] → 0 , t → + ∞
(2) (47) n + 9 n 2 − n 3 3 = n ( 1 − 1 − 9 n 3 ) = n ( 9 3 n + o ( 1 n ) ) → 3 , n → + ∞
(3) (48) sin x − arctan x tan x − arcsin x = ( x − x 3 6 + o ( x 3 ) ) − ( x − x 3 3 + o ( x 3 ) ) ( x + x 3 3 + o ( x 3 ) ) − ( x + x 3 6 + o ( x 3 ) ) → 1 , x → 0
(4) 解法一 :利用Stolz定理可得(49) LHS = lim n → + ∞ 1 2 n + 1 ln ( n + 1 ) − ln n = lim n → + ∞ n 2 n + 1 lim n → + ∞ ln [ ( 1 + 1 n ) n ] = 1 2
解法二 :利用此前证明过的(50) 1 + 1 2 + ⋯ + 1 n = ln n + γ + o ( 1 ) , n → + ∞ (51) LHS = [ ln ( 2 n ) + γ + o ( 1 ) ] − 1 2 [ ln n + γ + o ( 1 ) ] ln n = 1 2 ln n + O ( 1 ) ln n → 1 2 , n → + ∞ ◻
例 7.3.15
求 sec x := 1 cos x 在 x = 0 处带4阶Peano余项的Taylor展开式。
(52) cos x = 1 − x 2 2 + x 4 24 + o ( x 4 ) , x → 0 (53) sec x = 1 1 − x 2 2 + x 4 24 + o ( x 4 ) = 1 + x 2 2 + 5 x 4 24 + o ( x 4 ) , x → 0 ◻
例 7.3.16
(第八届百度数学吧吧赛大学非数组 · 法官)设 f : R → R ,称 f 在 x 0 ∈ R 处拟递增,若存在一个趋于 0 的正序列 { h n } 使得 (54) lim n → + ∞ f ( x 0 + h n ) − f ( x 0 ) h n ≥ 0
(1)
试构造 f ∈ C ( R ) ,满足 f 在 x = 0 处拟递增,但 f 在任意包含 x = 0 的区间内不单调。
(2)
设 f ∈ C ( R ) ,且在任意 x 0 ∈ R 处拟递增,证明: f 在 R 上单调递增。
(55) f ( x ) = { x sin 1 x , x ≠ 0 0 , x = 0 , h n = 1 n π , lim n → + ∞ f ( 0 + h n ) − f ( 0 ) h n = 0 f x = 0 f [ 1 2 ( n + 1 ) π , 1 2 n π ]
(2) 设x 1 > x 0 k := f ( x 1 ) − f ( x 0 ) x 1 − x 0 (56) F ( x ) = f ( x ) − f ( x 0 ) − k ( x − x 0 ) F ( x 0 ) = F ( x 1 ) = 0 F [ x 0 , x 1 ] ∃ ξ ∈ [ x 0 . x 1 ) F ( ξ ) ∀ x ∈ ( ξ , x 1 ) (57) 0 ≥ F ( ξ ) − F ( x ) ξ − x = f ( ξ ) − f ( x ) ξ − x − k ⟹ k ≥ f ( x ) − f ( ξ ) x − ξ ξ 0 { h n } lim n → + ∞ f ( ξ + h n ) − f ( ξ ) h n ≥ 0
取x = ξ + h n (58) f ( x 1 ) − f ( x 0 ) x 1 − x 0 = k ≥ lim n → + ∞ f ( ξ + h n ) − f ( ξ ) h n ≥ 0 f ( x 1 ) ≥ f ( x 0 ) f R ◻
例 7.3.17
设 x 0 ∈ ( 0 , 1 ) , x n + 1 = x n ( 1 − x n ) ,试证明: (59) x n = 1 n − ln n n 2 + O ( 1 n 2 )
{ x n } n = 1 0 lim n → + ∞ x n = 0 (60) 1 x n + 1 = 1 x n ( 1 − x n ) = 1 x n + 1 + x n + O ( x n 2 ) = 1 x n + O ( 1 ) (61) 1 x n = O ( n ) ⟹ x n = O ( 1 n ) (62) 1 x n + 1 = 1 x n + 1 + O ( 1 n ) (63) 1 x n = n + O ( ln n ) ⟹ x n = 1 n + O ( ln n n 2 ) (64) 1 x n + 1 = 1 x n + 1 + 1 n + O ( ln n n 2 ) (65) 1 x n = n + ln n + O ( 1 ) ⟹ x n = 1 n − ln n n 2 + O ( 1 n 2 ) ◻
∑ k = 1 n O ( 1 ) ≠ O ( n ) ∑ k = 1 n k = O ( n 2 ) O k
例 7.3.18
设 x 0 ∈ ( 0 , 1 ) , x n + 1 = x n ( 1 − x n ) 。
(1)
证明: lim n → + ∞ x n 存在,并求出该极限值。
(2)
计算: lim n → + ∞ n x n 。
(3)
计算: lim n → + ∞ n ( 1 − n x n ) ln n 。
{ x n } n = 1 0 lim n → + ∞ x n = 0
(2) 由Stolz定理可得(66) lim n → + ∞ n x n = lim n → + ∞ n 1 x n = lim n → + ∞ 1 1 x n + 1 − 1 x n = lim n → + ∞ x n 2 ( 1 − x n ) x n 2 = 1
(3) 结合(2)的结论,由Stolz定理可得(67) lim n → + ∞ n ( 1 − n x n ) ln n = lim n → + ∞ 1 − n x n x n ln n = lim n → + ∞ 1 x n − n ln n = lim n → + ∞ 1 x n + 1 − 1 x n − 1 ln ( n + 1 ) − ln n = lim n → + ∞ x n − x n + 1 − x n x n + 1 x n x n + 1 1 n = lim n → + ∞ x n 3 x n 3 ( 1 − x n ) = 1 ◻
例 7.3.19
设 x 0 ∈ R , x n + 1 = sin x n ,试证明: (68) x n 2 = 3 n − 9 ln n 5 n 2 + O ( 1 n 2 ) 提示: csc 2 x 在 x = 0 附近的渐近展开为 (69) csc 2 x = 1 x 2 + 1 3 + x 2 15 + O ( x 4 ) , x → 0
{ x n } 0 lim n → + ∞ x n = 0 csc 2 x (70) 1 x n + 1 2 = 1 x n 2 + 1 3 + x n 2 15 + O ( x n 4 ) = 1 x n 2 + O ( 1 ) (71) 1 x n 2 = O ( n ) ⟹ x n 2 = O ( 1 n ) (72) 1 x n + 1 2 = 1 x n 2 + 1 3 + O ( 1 n ) (73) 1 x n 2 = 1 3 n + O ( ln n ) ⟹ x n 2 = 3 n + O ( ln n n 2 ) (74) 1 x n + 1 2 = 1 x n 2 + 1 3 + 1 5 n + O ( ln n n 2 ) (75) 1 x n 2 = 1 3 n + 1 5 ln n + O ( 1 ) ⟹ x n 2 = 3 n − 9 ln n 5 n 2 + O ( 1 n 2 ) ◻
例 7.3.20
设 x 0 ∈ R , x n + 1 = sin x n 。
(1)
证明: lim n → + ∞ x n 存在,并求出该极限值。
(2)
计算: lim n → + ∞ n x n 2 。
(3)
计算: lim n → + ∞ n ( 3 − n x n 2 ) ln n 。
{ x n } 0 lim n → + ∞ x n = 0
(2) 由Stolz定理可得(76) lim n → + ∞ n x n 2 = lim n → + ∞ n 1 x n 2 = lim n → + ∞ 1 1 x n + 1 2 − 1 x n 2 = lim n → + ∞ sin 2 x n 1 − ( 1 − 1 6 x n 2 + o ( x n 2 ) ) 2 = 3
(3) 结合(2)的结论,由Stolz定理可得(77) lim n → + ∞ n ( 3 − n x n 2 ) ln n = 3 lim n → + ∞ 3 − n x n 2 x n 2 ln n = 3 lim n → + ∞ 3 x n 2 − n ln n = 3 lim n → + ∞ 3 x n + 1 2 − 3 x n 2 − 1 ln ( n + 1 ) − ln n = 3 lim n → + ∞ 3 − 3 ( 1 − 1 6 x n 2 + 1 120 x n 4 ) 2 − ( x n − 1 6 x n 3 ) 2 + o ( x n 4 ) 1 n sin 2 x n = 9 lim n → + ∞ 1 5 x n 4 + o ( x n 4 ) x n 4 = 9 5 ◻
例 7.3.21
(高等微积分 · 作业)设函数 f : [ 0 , 1 ] → [ 0 , 1 ] 严格单调递增,且满足:
∀ b ≥ 1 ,都有 f ( 1 b ) < 1 b + 1 ;
∀ t > 1 , ∃ M ≥ 1 ,使得 b ≥ M ⟹ f ( 1 b ) > 1 b + t 。
设 a 1 ∈ ( 0 , 1 ) ,定义数列 { a n } n ≥ 1 满足 a n + 1 = f ( a n ) ,证明: lim n → + ∞ n a n = 1 。
x = 1 b ε = t − 1 δ = 1 M f ∀ ε > 0 ∃ δ > 0 (78) 0 < x < δ ⟹ 1 < 1 f ( x ) − 1 x < 1 + ε ⟹ lim x → 0 + [ 1 f ( x ) − 1 x ] = 1 0 < x ≤ 1 ⟹ 0 ≤ f ( 0 ) < f ( x ) < x 1 + x < x
令x → 0 + f ( 0 ) = 0 0 < x ≤ 1 ⟹ 0 < f ( x ) < x x = 0 f [ 0 , 1 ] a 1 ∈ ( 0 , 1 ) (79) 0 < a n + 1 = f ( a n ) < a n 1 + a n < a n { a n } 0 lim n → + ∞ a n = x ∗ x ∗ = f ( x ∗ ) x ∗ = 0
由于1 a n + ∞ (80) lim n → + ∞ n a n = lim n → + ∞ n 1 a n = lim n → + ∞ 1 1 a n + 1 − 1 a n = lim x → 0 + 1 1 f ( x ) − 1 x = 1 ◻
例 7.3.22
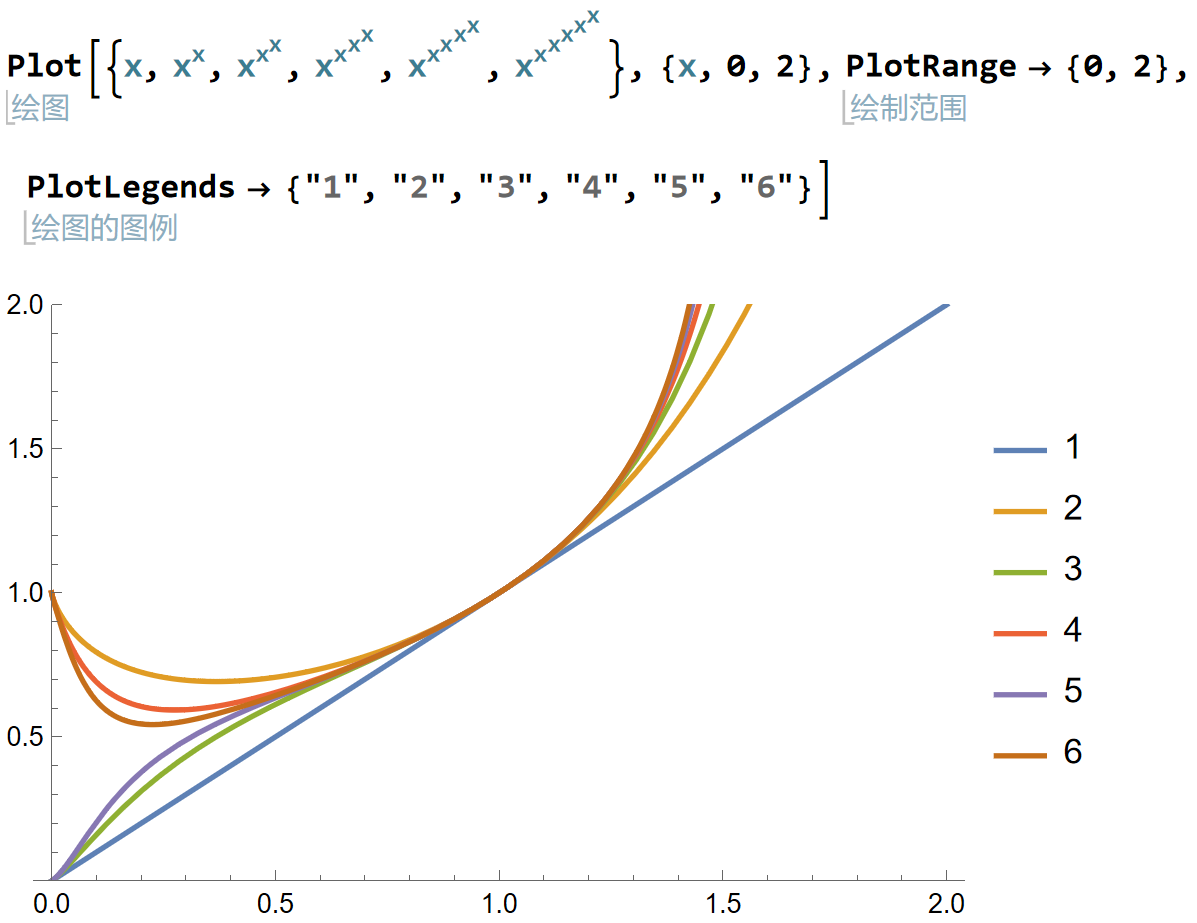
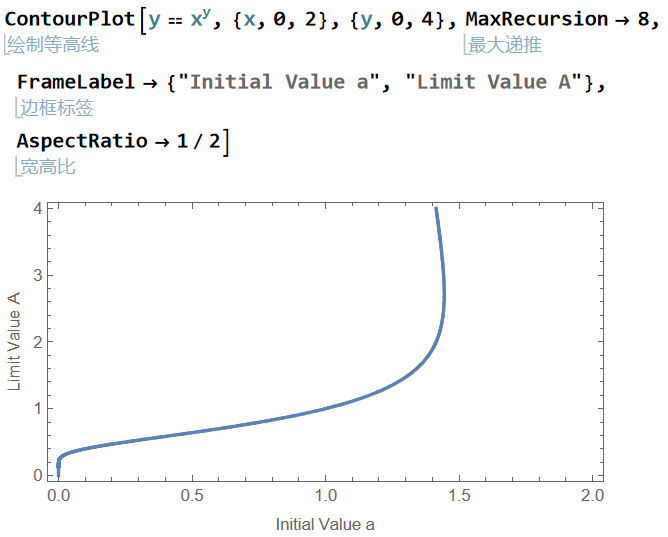
(2023秋期中考试拓展)设 a ∈ ( 0 , + ∞ ) , x 1 = a , x n + 1 = a x n 。若 lim n → + ∞ x n 存在,求 a 的取值范围,并求出该极限值。
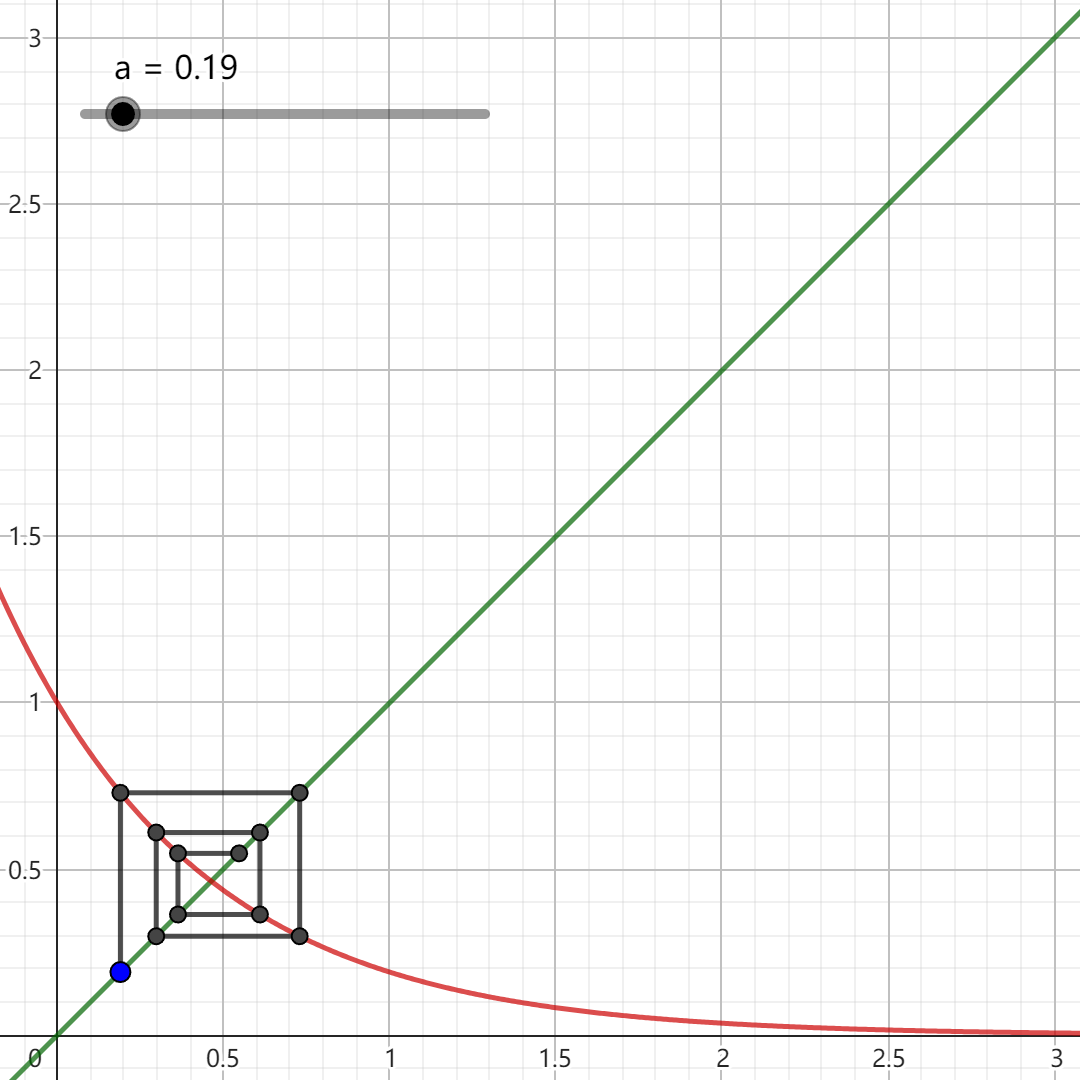
图 7.3.1: 验证极限的存在性
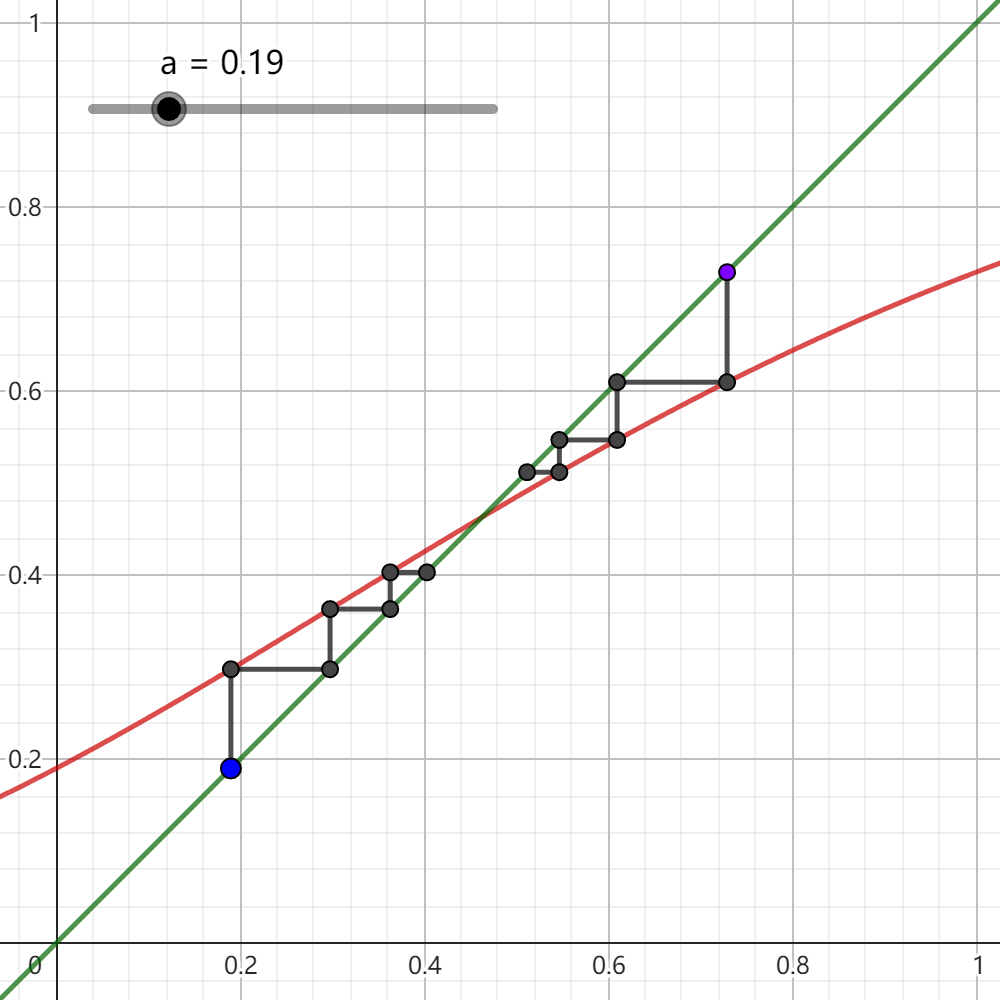
图 7.3.2: 数列的迭代图
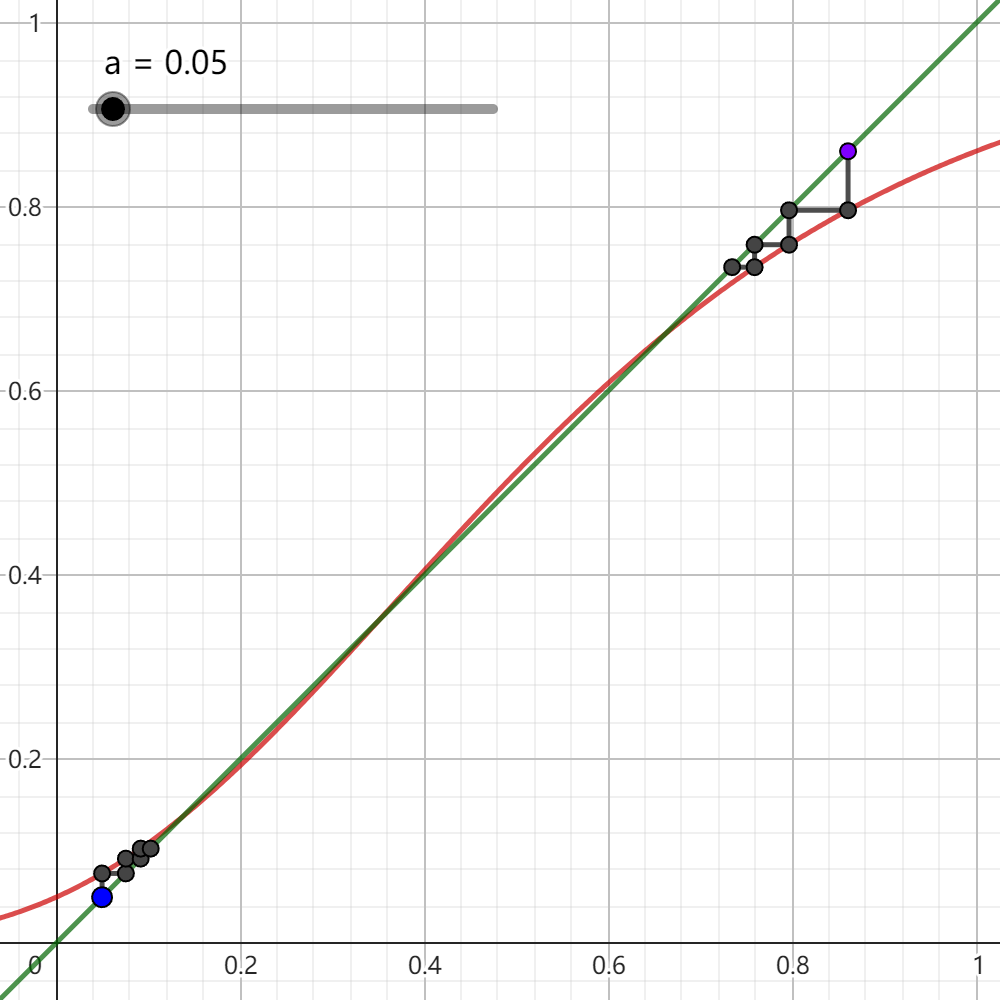
图 7.3.3: 数列的二阶迭代图
(1) 归纳可证x n = a ↑ n = a a ⋅ ⋅ ⋅ a ⏟ n f ( x ) = x ↑ n 图像 出发,如图7.3.1 (a)所示。
当x f ( x )
当x x ↑ ( 2 k + 1 ) x = 0 + 0 x ↑ ( 2 k ) x = 0 + 1 k ∈ N
当x
因此我们可以朴素地猜想:a
(2) 我们再来考察数列的极限值 。假设数列收敛,且极限为正数A (81) A = lim n → + ∞ x n + 1 = lim n → + ∞ a x n = a A a A A = a A 7.3.1 (b)所示。我们容易发现,图像有一个明显的右边界,当a a ≤ e 1 / e
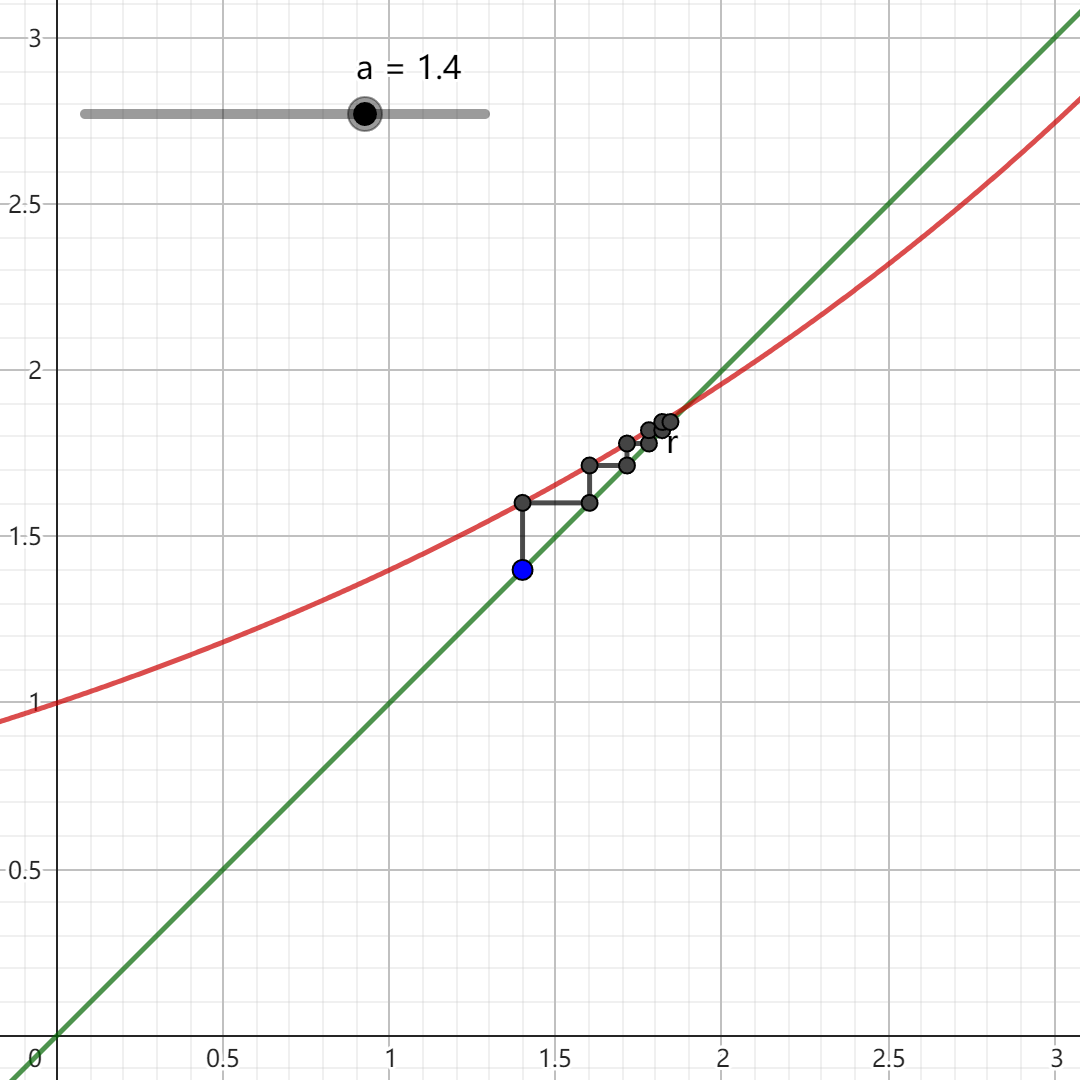
(3) 我们注意到这是一个不动点迭代的形式,故我们最后考察数列的不动点迭代图,又称“蛛网图”,即不断将( x n , x n ) ( x n , x n + 1 = f ( x n ) ) y = x y = f ( x ) 7.3.2 所示。图中蓝色的点为迭代起点。观察可知:
当a > 1
当a > 1 y = a x y = x a = e 1 / e
当0 < a < 1
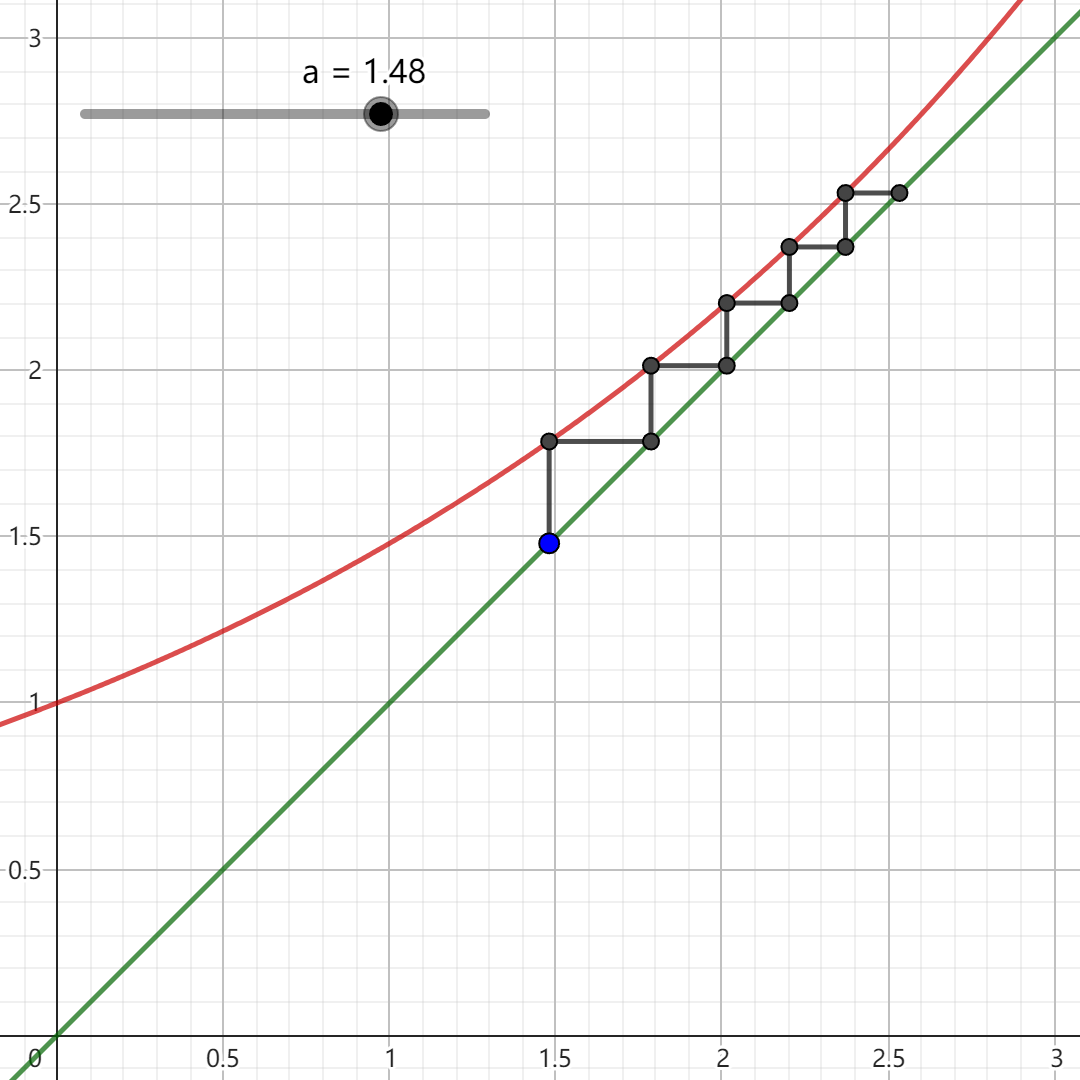
这启发我们研究这两个子列的迭代模式,故我们接下来考虑二阶迭代x n + 2 = g ( x n ) := a a x n 7.3.3 所示。图中蓝色的点为奇数项子列的迭代起点,紫色的点为偶数项子列的迭代起点。观察可知:
当a < 1 y = a a x y = x g
当a < 1 g { x n } 0 1 a 0 < a < e − e
整理好以上思路,我们开始证明。由于证明过程涉及两个不动点迭代函数y = a x y = a a x
推论 7.3.23
(1) 设 a > 0 ,则 y = a x 与 y = x 的交点个数为 (82) { 2 , 1 < a < e 1 / e 1 , a = e 1 / e ∨ 0 < a ≤ 1 0 , a > e 1 / e 且当 1 < a < e 1 / e 时,设两个交点的横坐标为 x 1 ∗ < x 2 ∗ ,则有 x 1 ∗ < 1 ln a < x 2 ∗ 。
(2) 设 a > 0 ,则 y = a a x 与 y = x 的交点个数为 (83) { 3 , 0 < a < e − e 2 , 1 < a < e 1 / e 1 , e − e ≤ a ≤ 1 ∨ a = e 1 / e 0 , a > e 1 / e 且当 e − e ≤ a < 1 时,设唯一交点的横坐标为 x ∗ ,则有 a < x ∗ < a a 且 a x ∗ = x ∗ ;当 0 < a < e − e 时,设三个交点的横坐标为 x 1 ∗ < x ∗ < x 2 ∗ ,则有 a < x 1 ∗ < x ∗ < x 2 ∗ < a a 且 a x ∗ = x ∗ 。
a x a a x
(1) 设函数f ( x ) = x ln a − ln x f ′ ( x ) = ln a − 1 x 0 < a ≤ 1 f R + f ( 0 + ) = + ∞ f ( 1 ) = ln a < 0 f ( 0 , 1 ) y = a x y = x ( 0 , 1 )
当a > 1 f ( 0 , 1 ln a ] [ 1 ln a , + ∞ ) f (84) f ( 1 ln a ) = 1 − ln 1 ln a = 1 + ln ln a f ( 1 ) = ln a > 0 f ( + ∞ ) = + ∞
当1 + ln ln a > 0 a > e 1 / e f
当a = e 1 / e f x = 1 ln a = e ( e , e )
当1 < a < e 1 / e f x 1 ∗ ∈ ( 0 , 1 ln a ) , x 2 ∗ ∈ ( 1 ln a , + ∞ ) x 1 ∗ < 1 ln a < x 2 ∗
(2) 当a = 1 y = a a x y = x a > 1 (85) { a x > x ⟹ a a x > a x > x a x < x ⟹ a a x < a x < x a x = x ⟹ a a x = a x = x y = a a x − x y = a x − x 1 < a < e 1 / e y = a a x y = x a = e 1 / e y = a a x y = x a > e 1 / e y = a a x y = x
当0 < a < 1 g ( x ) = x ln a − ln ln x ln a g ′ ( x ) = ln a − 1 x ln x x ln x e − 1 − e − 1
当1 ln a > e 0 < a < e − e g ′ ξ 1 , ξ 2 ξ 1 ln ξ 1 = ξ 2 ln ξ 2 = 1 ln a ξ 1 < 1 e < ξ 2 g ( 0 , ξ 1 ] [ ξ 1 , ξ 2 ] [ ξ 2 , 1 ) ln a (86) g ( ξ i ) = ξ i ln a − ln ln ξ i ln a = − ln ξ i + 1 ln ξ i − 2 ln ( − ln ξ i ) , i = 1 , 2 t i = − ln ξ i t 1 > 1 > t 2 h ( t ) = t − 1 t − 2 ln t (87) h ′ ( t ) = 1 + 1 t 2 − 2 t = ( t − 1 ) 2 t > 0 , t ≠ 1 h ( t ) R + (88) g ( ξ 2 ) = h ( t 2 ) < h ( 1 ) = 0 < h ( t 1 ) = g ( ξ 1 ) g ( a ) = a ln a < 0 g ( a a ) = ( a a − 1 ) ln a > 0 ∃ x 1 ∗ ∈ ( a , ξ 1 ) x ∗ ∈ ( ξ 1 , ξ 2 ) x 2 ∗ ∈ ( ξ 2 , a a ) g x # y = a x y = x x # ∈ { x 1 ∗ , x ∗ , x 2 ∗ } (89) f ( ξ i ) = ξ i ln a − ln ξ i = 1 − ln 2 ξ i ln ξ i = t i 2 − 1 t i ⟹ f ( ξ 1 ) > f ( x # ) = 0 > f ( ξ 2 ) f R + a < x 1 ∗ < ξ 1 < x # < ξ 2 < x 2 ∗ < a a x ∗ = x # a x ∗ = x ∗
当1 ln a ≤ e e − e ≤ a < 1 g ′ > 0 x ≠ 1 e g R + g ( a ) = a ln a < 0 g ( a a ) = ( a a − 1 ) ln a > 0 g ( a , a a ) x ∗ x ∗ = a x ∗
◻
1 ∘ a = 1 { x n } 1
2 ∘ 1 < a ≤ e 1 / e x ∗ a x = x x 2 = a a > a = x 1 (90) x n + 2 = a x n + 1 > a x n = x n + 1 , n ∈ N { x n } (91) x n + 1 = a x n ≤ a x ∗ = x ∗ , n ∈ N { x n } x ∗ { x n } ξ a x = x a n ≤ x ∗ n → + ∞ ξ ≤ x ∗ ξ ≥ x ∗ x ∗ ξ = x ∗
3 ∘ a > e 1 / e (92) a x ≥ f ′ ( x ∗ ) ( x − x ∗ ) + f ( x ∗ ) , x ∈ R x ∗ (93) f ′ ( x ∗ ) = a x ∗ ln a = 1 ⟹ x ∗ = − ln ln a ln a (94) a x ≥ x − x ∗ + f ( x ∗ ) = x + ln ln a + 1 ln a a > e 1 / e ln ln a + 1 ln a > 0 (95) x n + 1 = a x n ≥ x n + ln ln a + 1 ln a ≥ a + n ln ln a + 1 ln a , n ∈ N n → + ∞ x n → + ∞
也可采用反证法 。假设当a > e 1 / e { x n } ξ a x = x a > e 1 / e
4 ∘ 0 < a < 1 x 1 ∗ , x 2 ∗ a a x = x x ∗ a x = x x n + 2 = a a x n x 1 = a < x ∗ < a a = x 2 x # a a x = x (96) { x n + 2 > x n ⟹ x n + 4 = a a x n + 2 > a a x n = x n + 2 x n + 2 < x n ⟹ x n + 4 = a a x n + 2 < a a x n = x n + 2 x n > x # ⟹ x n + 2 = a a x n > a a x # = x # x n < x # ⟹ x n + 2 = a a x n < a a x # = x # x 3 = a a a > a 1 = x 1 x 4 = a x 3 < a x 1 = x 2 x 1 = a < x 1 ∗ x 2 = a a > x 2 ∗ { x n } x 1 ∗ x 2 ∗ ξ 1 , ξ 2 x 2 k − 1 < ξ 1 ≤ ξ 2 < x 2 k ′ ∀ k , k ′ ∈ N ∗ k , k ′ → + ∞ ξ 1 ≤ x 1 ∗ ≤ x 2 ∗ ≤ ξ 2 ξ 1 , ξ 2 a a x = x x 1 ∗ ≤ ξ 1 ≤ ξ 2 ≤ x 2 ∗ x 1 ∗ , x 2 ∗ a a x = x ξ 1 = x 1 ∗ ≤ x 2 ∗ = ξ 2
当e − e ≤ a < 1 x 1 ∗ = x ∗ = x 2 ∗ x ∗ x ∗
当0 < a < e − e x 1 ∗ < x ∗ < x 2 ∗
综上所述 ,lim n → + ∞ x n e − e ≤ a ≤ e 1 / e x ∗ x ∗ = a x ∗ ◻
[prev ] [up ]