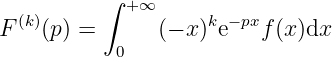3.4 Applications of integral depending on a parameter
Integral transformation: function function where
where is called the kernal of the integral transformation. Analogy. Assuming is discrete,
i.e.
Similarly,
then we have
So integral transformation is the extension of linear transformation from finite dimension to infinite
dimension.
Particularly, if has a form of , then
is called the convolution of and . At this time
Example 3.4.1 The boundary value problem of Laplace function. Assuming , then
Assuming
we can verify that
- .
- .
- .
Assuming is continuous and bounded (within ), let
Then we have
Laplacian transformation.
If such that , , then the Laplacian transformation exists when and (Note: maybe is only
integrable!). We can prove that
Consider
So we have
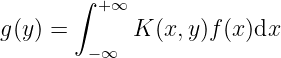
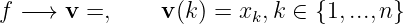
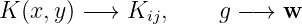
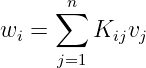
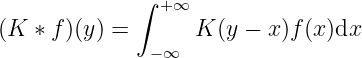
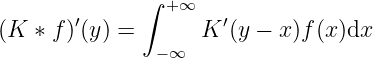

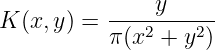
![∫ ∫
+∞ y +∞
u(x,y ) = π-[(x-−-t)2 +-y2]f (t)dt = K (x − t,y)f(t)dt
−∞ −∞](main208x.png)
 = e f(x)dx = F (p)
0](main209x.png)