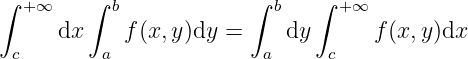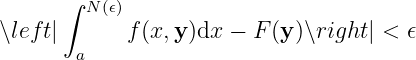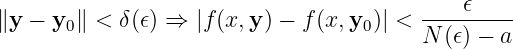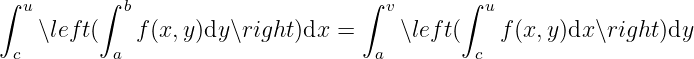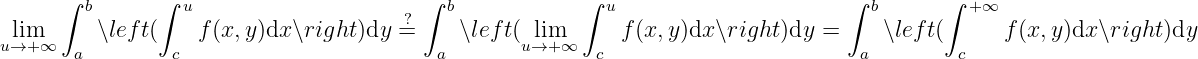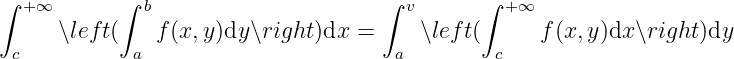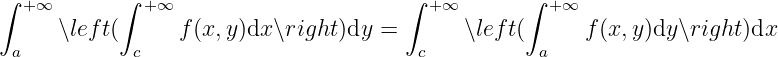General integral depending on a parameter

3.2 General integral depending on a parameter

General integral depending on a parameter.

Integral on infinite interval.
Unbounded function (improper integral).

What we’re interested are integrals like

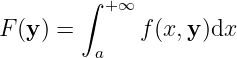
∫ +∞ F(y ) = f(x, y)dx a

Definition 3.2.1 $\int_{a}^{+ \infty} f (x, y) d x$ is uniformly convergent with respect to $y \in U$ if

$\forall y \in U$ , $\exists F (y) \in R$ such that $\forall ϵ > 0$ , $\exists N (ϵ, y) > a$ such that $\forall A > N (ϵ, y)$ ,
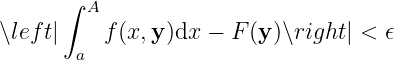
$∫ A ∖left| f(x, y)dx − F (y)∖right| < 𝜖 a$
i.e. $\int_{a}^{+ \infty} f (x, y) d x$ is pointwisely convergent with respect to $y$ for any $y \in U$ .
It is uniformly convergent with respect to $y$ , $N (ϵ, y)$ mentioned above has nothing to do with $y$ , i.e. $\forall ϵ > 0$ , $\exists N (ϵ) > a$ such that $\forall y \in U$ , $\forall A > N (ϵ)$ , $\exists F (y) \in R$ such that
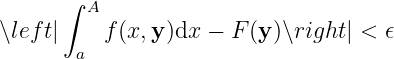
$∫ A ∖left| f(x, y)dx − F (y)∖right| < 𝜖 a$

Continuity. Consider $\begin{aligned} | F (y) - F (y_{0}) | & = | \int_{a}^{+ \infty} f (x, y) d x - \int_{a}^{+ \infty} f (x, y_{0}) d x | \\ \leq \int_{a}^{+ \infty} | f (x, y) - f (x, y_{0}) | d x \leq \int_{a}^{+ \infty} ϵ d x = ? \end{aligned}$

For general integrals, we cannot avoid discussing its convergence.

Theorem 3.2.2 Assuming $f : [a, + \infty) \times U \to R$ where $U \subseteq R^{n}$ satisfies

$F (y) = \int_{a}^{+ \infty} f (x, y) d x$ is uniformly convergent on $U$ with respect to $y$ .
$\forall x \geq a$ , $f (x, y)$ is continuous at $y_{0}$ with respect to $y$ , and is uniformly continuous on any bounded closed interval $[a, b]$ with respect to $x$ , i.e. $\forall ϵ > 0$ , $\exists δ (ϵ, [a, b]) > 0$ such that $\forall x \in [a, b]$ and $\forall y \in U$ ,
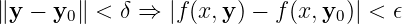
$∥y − y0∥ < δ ⇒ |f(x,y) − f(x, y0)| < 𝜖$

Then $F$ is continuous at $y_{0}$ .

Proof $\forall ϵ > 0$ , $\exists N (ϵ) > a$ such that $\forall y \in U$ ,

∫ N (𝜖) ∖left| f (x, y)dx − F (y)∖right| < 𝜖 a

For $[a, N (ϵ)]$ , $\exists δ (ϵ) > 0$ such that $\forall x \in [a, N (ϵ)]$ and $\forall y \in U$ ,

𝜖 ∥y − y0 ∥ < δ(𝜖) ⇒ |f(x,y ) − f (x,y0)| <--------- N (𝜖) − a

Then we have $\begin{aligned} | F (y) - F (y_{0}) | & \leq | F (y) - \int_{a}^{N (ϵ)} f (x, y) d x | + | \int_{a}^{N (ϵ)} f (x, y) d x - \int_{a}^{N (ϵ)} f (x, y_{0}) d x | \\ + | \int_{a}^{N (ϵ)} f (x, y_{0}) d x - F (y_{0}) | \\ \leq ϵ + \int_{a}^{N (ϵ)} | f (x, y) - f (x, y_{0}) | d x + ϵ, ∥ y - y_{0} ∥ < δ (ϵ) \\ \leq 3 ϵ \end{aligned}$

Hence, $F$ is continuous at $y_{0}$ . $◻$

Derivability.

Theorem 3.2.3 Given $y_{0} \in U$ where $U \subseteq R^{n}$ is an open set. Assuming $f : [a, + \infty) \times U \to R$ satisfies

$\int_{a}^{+ \infty} f (x, y_{0}) d x$ is convergent.
$\forall 1 \leq k \leq n$ , $\frac{\partial f}{\partial y_{k}} (x, y)$ is continuous with respect to $(x, y)$ and $\int_{a}^{+ \infty} \frac{\partial f}{\partial y_{k}} (x, y) d x$ is uniformly convergent with respect to $y \in U$ .

Then in a certain neighborhood $V$ of $y_{0}$ , $\int_{a}^{+ \infty} f (x, y) d x$ is uniformly convergent and of $C^{1}$ with respect to $y \in V$ , and $\forall 1 \leq k \leq n$ , the order of the derivative and the general integral could be exchanged, i.e.

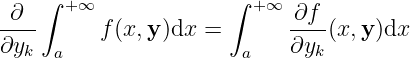
∫ ∫ ∂ +∞ +∞ ∂f ---- f(x, y)dx = ----(x,y)dx ∂yk a a ∂yk

Proof Mark $\begin{aligned} F (y) = \int_{a}^{+ \infty} f (x, y) d x, & F_{A} (y) = \int_{a}^{A} f (x, y) d x \\ G_{k} (y) = \int_{a}^{+ \infty} \frac{\partial f}{\partial y_{k}} (x, y) d x, & G_{A, k} (y) = \int_{a}^{A} \frac{\partial f}{\partial y_{k}} (x, y) d x \end{aligned}$

Here the existence of $F (y)$ is unknown except $F (y_{0})$ ! Target:

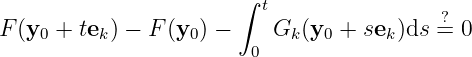
∫ t F (y0 + tek) − F(y0) − Gk (y0 + sek)ds =?0 0

Since the existence of the first term is unknown, we consider $\begin{aligned} I & = | F_{A} (y_{0} + t e_{k}) - F (y_{0}) - \int_{0}^{t} G_{k} (y_{0} + s e_{k}) d s | \to_{Prove}^{A \to + \infty} 0 \\ \leq | F_{A} (y_{0} + t e_{k}) - F_{A} (y_{0}) - \int_{0}^{t} G_{k} (y_{0} + s e_{k}) d s | + | F_{A} (y_{0}) - F (y_{0}) | \\ \leq \int_{0}^{t} | \frac{\partial F_{A}}{\partial y_{k}} (y_{0} + s e_{k}) - G_{k} (y_{0} + s e_{k}) | d s + | F_{A} (y_{0}) - F (y_{0}) | \\ = \int_{0}^{t} | \int_{a}^{A} \frac{\partial f}{\partial y_{k}} (x, y_{0} + s e_{k}) d x - \int_{a}^{+ \infty} \frac{\partial f}{\partial y_{k}} (x, y_{0} + s e_{k}) d x | d s + | F_{A} (y_{0}) - F (y_{0}) | \end{aligned}$

Notice that $\forall ϵ > 0$ , $\exists N (ϵ) > a$ such that $\forall A > N (ϵ)$ , $\forall y \in U$ , $\begin{aligned} | \int_{a}^{A} \frac{\partial f}{\partial y_{k}} (x, y) d x - \int_{a}^{+ \infty} \frac{\partial f}{\partial y_{k}} (x, y) d x | & < ϵ \\ | \int_{a}^{A} f (x, y_{0}) d x - \int_{a}^{+ \infty} f (x, y_{0}) d x | & < ϵ \end{aligned}$

Therefore, we have

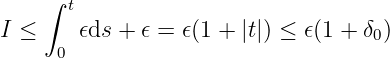
∫ t I ≤ 𝜖ds + 𝜖 = 𝜖(1 + |t|) ≤ 𝜖(1 + δ0) 0

where $δ_{0}$ is only related to $y_{0}$ . Terminally

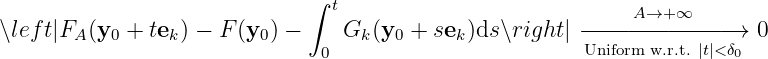
∫ t A→+ ∞ ∖left|FA (y0 + tek) − F (y0) − Gk (y0 + sek)ds∖right| −−Un−i−fo−r−m w−.−r−.t−. |t−|<−→δ0 0 0

i.e.

∫ ∫ ∫ ∫ +∞ +∞ t +∞ -∂f- f(x,y0 + tek)dx = f (x,y0)dx + ∖lef t[ ∂y (x,y0 + sek)dx ∖right ]ds a a 0 a k

and it’s uniformly convergent with respect to $| t | < δ_{0}$ , meaning we could do the derivative and $\forall | t | < δ_{0}$ ,

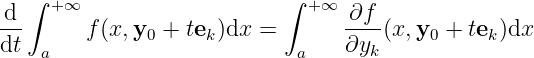
∫ + ∞ ∫ +∞ -d- ∂f-- dt a f(x,y0 + tek)dx = a ∂yk(x,y0 + tek)dx

When $t = 0$ , we have

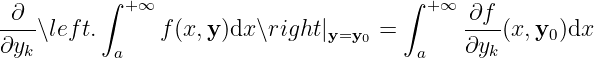
∫ ∫ -∂-- +∞ + ∞ ∂f-- ∂y ∖left. f(x,y )dx∖right|y=y0 = ∂y (x,y0)dx k a a k

The selection of $e_{k}$ is arbitrary, and the conditions of binary continuous and uniformly convergent guarantee the step-by-step move of $y$ , meaning $\frac{\partial}{\partial y_{k}} \int_{a}^{+ \infty} f (x, y) d x$ is continuous with respect to $y$ ( $C^{1}$ proved). $◻$

Integrability.

Theorem 3.2.4 Assuming $f : [c, + \infty) \times [a, b] \to R$ is continuous, $\int_{c}^{+ \infty} f (x, y) d x$ is uniformly convergent with respect to $y \in [a, b]$ , then $\int_{c}^{+ \infty} d x \int_{a}^{b} f (x, y) d y$ is convergent, and

∫ +∞ ∫ b ∫ b ∫ +∞ dx f (x,y)dy = dy f (x,y)dx c a a c

Proof $\forall ϵ > 0$ , $\exists N (ϵ) > c$ such that $\forall D > C > N (ϵ)$ , $\forall y \in [a, b]$ , $| \int_{C}^{D} f (x, y) d x | < ϵ$ . Consider $\begin{aligned} I & = | \int_{C}^{D} (\int_{a}^{b} f (x, y) d y) d x | = | \int_{a}^{b} (\int_{C}^{D} f (x, y) d x) d y | \\ \leq \int_{a}^{b} | \int_{C}^{D} f (x, y) d x | d y \leq ϵ (b - a) \end{aligned}$

Known

∫ u ∫ b ∫ v ∫ u ∖lef t( f(x,y)dy ∖right)dx = ∖left( f(x,y)dx ∖right)dy c a a c

Let $u \to + \infty$ , left-handed side is the definition of general integral; as for the right-handed side,

∫ b ∫ u ∫ b ∫ u ∫ b ∫ + ∞ lim ∖left( f(x,y)dx ∖right)dy ?= ∖left( lim f (x, y)dx∖right )dy = ∖lef t( f(x,y)dx ∖right)dy u→+ ∞ a c a u→+ ∞ c a c

Therefore,

∫ +∞ ∫ b ∫ v ∫ +∞ ∖lef t( f(x,y)dy ∖right)dx = ∖left( f(x,y)dx ∖right)dy c a a c

Why $(?)$ is true? It could be regarded as a kind of continuity, let $t = \frac{1}{u}$ to get the result. $◻$

Theorem 3.2.5 Assuming $f : [c, + \infty) \times [a, + \infty) \to R$ is continuous, $\int_{c}^{+ \infty} f (x, y) d x$ and $\int_{a}^{+ \infty} f (x, y) d y$ are both uniformly convergent, then for the equality below

∫ +∞ ∫ +∞ ∫ +∞ ∫ + ∞ ∖lef t( f(x,y )dx ∖right)dy = ∖left( f(x,y)dy ∖right)dx a c c a

If at least one side of the equality exists, then both sides exist and they are equivalent.

Proof is left as exercise. :)