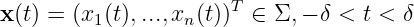Curve and surface

2.6 Curve and surface

Definition 2.6.1 $γ \in R^{n}$ is a curve if there exists $x : (a, b) \to R^{n}$ of $C^{k}$ where $t \mapsto x (t)$ such that $γ = {x (t) | t \in (a, b)}$ . $x (t)$ is called a parameterization of $C^{k}$ of $γ$ . Mark

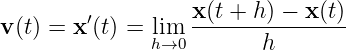
x(t + h ) − x (t) v (t) = x ′(t) = lim --------------- h→0 h

as the tangent vector of $γ$ at $x (t)$ .

Reparameterization. Given the parameterization

x (t), t \in (a, b)

γ

, let

t = t (s) \in C^{k}, s \in (α, β)

. Let

\tilde{x} (s) = x (t (s))

, then

γ = {\tilde{x} (s) | s \in (α, β)}

\tilde{v} = {\tilde{x}}^{'} (s) = {\tilde{x}}^{'} (t (s)) t^{'} (s) = v λ

where

t = λ s

. The tangent space of

γ

P_{0}

, marked as

T_{P_{0}} γ

, consists of all tangent vectors of

γ

P_{0}

Theorem 2.6.2 $T_{P_{0}} γ$ is a linear space. The tangent line of $γ$ at $P_{0}$ is $P_{0} + T_{P_{0}} γ$ . The relation between the tangent space and the tangent line is just the relation between the linear space and the affine space.

Curve equation.

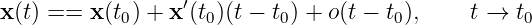
x (t) == x(t ) + x′(t )(t − t ) + o(t − t ), t → t 0 0 0 0 0

Tangent equation. $\begin{aligned} x & = x (t_{0}) + x^{'} (t_{0}) λ, & λ \in (- \infty, + \infty) \\ = x (t_{0}) + x^{'} (t_{0}) (t - t_{0}), & t \in (- \infty, + \infty) \end{aligned}$

Definition 2.6.3 $n$ is the norm vector of $γ$ at $P_{0}$ if $n ⊥ T_{P_{0}} γ$ . The norm space consists of all norm vectors of $γ$ at $P_{0}$ , i.e. ${n | ⟨ x^{'} (t_{0}), n ⟩ = 0}$ , which is a linear space of $(n - 1)$ -dimension. The norm surface of $γ$ at $P_{0}$ is $P_{0} +$ norm space.

Definition 2.6.4 Given $γ$ and its parameterization $x (t)$ which is a regular curve meaning $x (t) \neq 0, \forall t$ . The length function of arc is defined as $l : (a, b) \to (0, + \infty)$ where $l (t) = \int_{a}^{t} ∥ x^{'} (s) ∥ d s$ .

Since

l^{'} (t) = ∥ x^{'} (t) ∥ > 0

, so

l

is bijective, meaning

t = t (l)

exists. Thus,

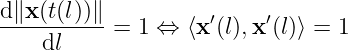
d ∥x(t(l))∥ ---------- = 1 ⇔ ⟨x′(l),x ′(l)⟩ = 1 dl

Take the derivative over $l$ to get

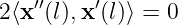
2⟨x ′′(l),x ′(l)⟩ = 0

Here $x^{″} (l)$ is called the principle norm vector, correspondingly other norm vectors are called subsidiary norm vectors.

Example 2.6.1 The graph of $z = f (x, y)$ where $f : E \to R, E \subseteq R^{2}$ is defined as

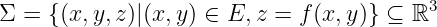
3 Σ = {(x,y,z)|(x,y) ∈ E,z = f(x,y)} ⊆ ℝ

It’s a 2-dimension surface.

Given $y = f (x_{1}, . . ., x_{n})$ , then

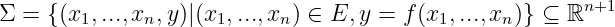
Σ = {(x1,...,xn,y )|(x1,...,xn) ∈ E, y = f(x1,...,xn )} ⊆ ℝn+1

is a $(n + 1)$ -dimension surface. Given $f : E \to R^{n}, E \subseteq R^{m}$ , then

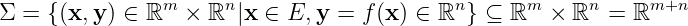
m n n m n m+n Σ = {(x,y) ∈ ℝ × ℝ |x ∈ E, y = f(x) ∈ ℝ } ⊆ ℝ × ℝ = ℝ

Definition 2.6.5 Given $Σ \subseteq R^{m}$ satisfying that $\forall P_{0} \in Σ$ , there exists a neighborhood $U \subseteq R^{n}$ of $P_{0}$ , the permutation (arrangement) $σ$ of $1, . . ., n$ and mapping $f$ of $C^{r}$ such that $Σ = {(x_{1}, . . ., x_{n}) \in R^{n} | (x_{σ (k + 1)}, . . ., x_{σ (n)}) = f (x_{σ (1)}, . . ., x_{σ (k)})}$ where $(x_{σ (1)}, . . ., x_{σ (k)})^{T} \in U \subseteq R^{k}$ and $U$ is open, then $Σ$ is called a $k$ -dimension surface of $C^{r}$ in $R^{n}$ .

Definition 2.6.6 A curve $γ$ of $C^{1}$ on $Σ$ passing through $P_{0}$ is defined as

T x (t) = (x1(t),...,xn(t)) ∈ Σ, − δ < t < δ

where $x (0) = P_{0}$ .

Definition 2.6.7 One of the tangent vectors of $Σ$ at $P_{0}$ is defined as $v = x^{'} (0)$ . The tangent space of $Σ$ at $P_{0}$ , $T_{P_{0}} Σ$ , is a set consisting of all tangent vectors of $Σ$ at $P_{0}$ .

Definition 2.6.8 $n$ is one of the norm vectors of $Σ$ at $P_{0}$ if

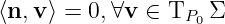
⟨n,v ⟩ = 0,∀v ∈ TP0 Σ

The norm space $N_{P_{0}} Σ$ is a set consisting of all norm vectors of $Σ$ at $P_{0}$ .

Theorem 2.6.9 Assuming $Σ$ is a $k$ -dimension surface of $C^{r}$ , then for any $P_{0} \in Σ$ , $T_{P_{0}} Σ$ is a $k$ -dimension linear space, $N_{P_{0}} Σ$ is a $(n - k)$ -dimension linear space and

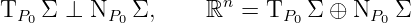
TP0 Σ ⊥ NP0 Σ, ℝn = TP0 Σ ⊕ NP0 Σ

Example 2.6.2

The graph of $C^{r}$ function/mapping is a surface.
$F : R^{m} \to R^{n}$ is a mapping of $C^{r}$ . $C \in R^{n}$ is a regular value of $F$ if for any $x_{0} \in F^{- 1} (C)$ , $\partial F (x_{0})$ is a full-row-rank matrix, i.e. all rows are linear independent, requiring $n \leq m$ .

According to IFT, there exists a permutation $σ$ of $1, . . ., n$ and mapping $g : R^{n - m} \to R^{n}$ of $C^{r}$ such that $F (x_{1}, . . ., x_{m}) = C \Leftrightarrow (x_{σ (1)}, . . ., x_{σ (n)}) = g (x_{σ (n + 1)}, . . ., x_{σ (m)})$ , then $Σ = F^{- 1} (C)$ is a $(m - n)$ -dimension surface of $C^{r}$ .
$x^{2} + y^{2} + z^{2} = R^{2}$ , construct $F (x, y, z) = x^{2} + y^{2} + z^{2} - R^{2} = 0$ , $\partial F (x, y, z) = (2 x, 2 y, 2 z) \neq (0, 0, 0)$ . It’s row-full-rank (with rank $1$ ), meaning $0$ is the regular value of $F$ . So $F$ determines a surface whose dimension is $3 - 1 = 2$ .
Surface.
$=$
Assuming $u (t)$ is of $C^{1}$ where $u (0) = u_{0}$ , $x (u_{0}) = P_{0}$ . $x (u (t)) \in Σ$ is of $C^{1}$ . Then
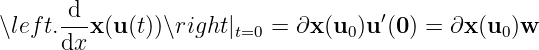
$d ′ ∖left.---x(u(t))∖right|t=0 = ∂x (u0)u (0) = ∂x (u0)w dx$
i.e. $u (t) = u_{0} + t w$ for any $w \in R^{k}$ .

Therefore $T_{P_{0}} Σ = {\partial x (u_{0}) w | w \in R^{k}} = {w_{1} \frac{\partial x}{\partial u_{1}} + . . . + w_{k} \frac{\partial x}{\partial u_{k}} | w_{1}, . . ., w_{k} \in R}$ is a $k$ -dimension linear space.

The tangent space is
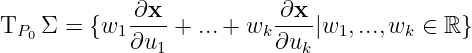
$T Σ = {w ∂x--+ ...+ w ∂x-|w ,...,w ∈ ℝ} P0 1∂u1 k ∂uk 1 k$
The tangent plane is
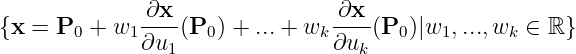
$∂x ∂x {x = P0 + w1 ----(P0) + ...+ wk ----(P0 )|w1, ...,wk ∈ ℝ} ∂u1 ∂uk$
Equation surface. Assuming
$∖lef t{ ∖right.$
Then $Σ : F^{- 1} (0) = {x | F (x) = 0}$ . Here
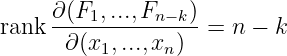
$∂(F1, ...,Fn−k) rank -∂-(x-,...,x-)- = n − k 1 n$
Assuming $x = x (t) = (x_{1} (t), . . ., x_{n} (t)$ is of $C^{1}$ . Then for any $t$ , $F (x (t)) = 0$ and $x (0) = P_{0}$ . Take the derivative over $t$ when $t = 0$ to get that $\partial F (P_{0}) x^{'} (0) = 0$ , i.e. $\partial F (P_{0}) v = 0$ .

Therefore the tangent space is
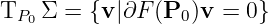
$TP0 Σ = {v|∂F (P0)v = 0}$
The tangent plane is
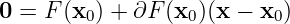
$0 = F (x0) + ∂F (x0)(x − x0)$
As for the norm vector, we have
$∖left{∖right. ⇔ ∖left{∖right.$
for any $v \in T_{P_{0}} Σ$ . Since $\nabla F_{1} (x_{0}), v, . . ., \nabla F_{n - k} (x_{0}), v$ is linear independent, the norm space is
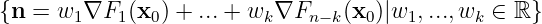
${n = w1 ∇F1 (x0) + ...+ wk∇Fn −k(x0)|w1, ...,wk ∈ ℝ }$
Parametric surface.
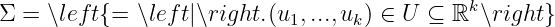
$Σ = ∖left{= ∖lef t|∖right.(u1,...,uk) ∈ U ⊆ ℝk∖right}$
is a $k$ -dimension surface of $C^{r}$ in $R^{n}$ if $x_{1}, . . ., x_{n}$ are all of $C^{r}$ . Here
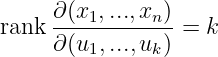
$rank ∂-(x1,...,xn) = k ∂(u1,...,uk)$
Easy to find that the tangent space is
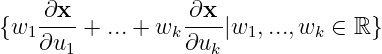
${w -∂x- + ...+ w -∂x-|w ,...,w ∈ ℝ} 1∂u1 k∂uk 1 k$
Assuming $k = n - 1$ and ${v_{1}, . . ., v_{n - 1}}$ is the set of bases of the tangent space. Hope to find $w$ s.t. $w ⊥ v_{i}$ , $i = 1, . . ., n - 1$ .

Construct a linear function $L (v) = det (v_{1}, . . ., v_{n - 1}, v) = ⟨ \nabla L, v ⟩, \forall v \in R^{n}$ . We have $⟨ \nabla L, v_{i} ⟩ = L (v_{i}) = det (v_{1}, . . ., v_{n - 1}, v_{i}) = 0$ . If $v_{1}, . . ., v_{n}$ are linear independent, then there exists $v_{n}$ such that $v_{1}, . . ., v_{n}$ are linear independent, here $L (v_{n}) \neq 0$ . Since $L$ is not constantly $0$ , so $\nabla L \neq 0$ .

Assuming $A_{i j}$ is the algebraic complement of the $i, j$ component, take
$v =$
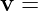
Then $L (v) = det (v_{1}, . . ., v_{n - 1}, v) = A_{1 n}^{2} + . . . + A_{n n}^{2} = ∥ v ∥^{2}$ . Notice that $L (\nabla L) = ⟨ \nabla L, \nabla L ⟩ = ∥ \nabla ∥^{2}$ , so $v = \pm \nabla L$ (proof detail is hidden).