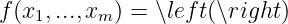Continuous mapping and function

1.3 Continuous mapping and function

Definition 1.3.1 A mapping $f : E \to R^{p} (E \subseteq R^{m})$ is continuous at $x_{0} \in E$ if for any $ϵ > 0$ , there exists $δ_{ϵ} > 0$ such that for any $x \in E$ subjecting to $∥ x - x_{0} ∥ < δ_{ϵ}$ , $∥ f (x) - f (x_{0}) ∥ < ϵ$ .

Theorem 1.3.2 A mapping $f : E \to R^{p} (E \subseteq R^{m})$ is continuous at $x_{0} \in E$ is equivalent to that for any $x_{n} \in E$ , $lim_{n \to + \infty} x_{n} = x_{0} \to lim_{n \to + \infty} f (x_{n}) = f (x_{0})$ .

Note When $n \to + \infty$ , $∥ x_{n} - x_{0} ∥ \to 0$ , $∥ f (x_{n}) - f (x_{0}) ∥ \to 0$ . The continuity has nothing to do with the selection of the norm.

Theorem 1.3.3 If $K \subseteq R^{m}$ is a bounded closed set, $f$ is continuous on $K$ meaning $f$ is continuous at any $x_{0} \in K$ , then $f (K) \subseteq R^{p}$ is also bounded closed. Particularly, if $p = 1$ , $f$ has the maximum and minimum on $K$ .

Proof For any $y_{n} \in f (K)$ , there exists $x_{n} \in K$ such that $y_{n} = f (x_{n})$ . Given $K$ is bounded closed, so there exists a convergent subsequence ${x_{n_{k}}}$ of ${x_{n}}$ such that $lim_{k \to + \infty} x_{n_{k}} = x_{0} \in K$ . $f$ is continuous at $x_{0} \in K$ , so $lim_{k \to + \infty} y_{n_{k}} = lim_{k \to + \infty} f (x_{n_{k}}) = f (x_{0}) \in f (K)$ . So $f (K)$ is bounded closed.

When $p = 1$ , $f (K) \subseteq R$ is bounded closed. Let $β = sup f (K)$ and $α = inf f (K)$ . $α, β$ cound be approached by sequences in the set $f (K)$ . Since $f (K)$ is closed, so $α, β \in f (K)$ , so $β = max f (K)$ and $α = min f (K)$ . $◻$

Definition 1.3.4 A set $E \subseteq R^{m}$ is a path-connected set if for any $a, b \in E$ , there exists a continuous mapping $x : [0, 1] \to R^{m}$ such that $x (0) = a, x (0) = b$ and for any $t \in [0, 1]$ , $x (t) \in E$ .

Theorem 1.3.5 If $E \subseteq R^{m}$ is a path-connected set, $f$ is continuous on $E$ , then $f (E) \subseteq R^{p}$ is also path-connected. Particularly, if $p = 1$ , $f (E)$ is a interval with intermediate value theorem.

Example 1.3.1 Continuous mappings and functions.

Constant mapping.
Linear mapping $L : R^{m} \to R^{p}$ . For any $x, y \in R^{m}$ , $\begin{aligned} ∥ L (x) - L (y) ∥ & = ∥ L (x - y) ∥ = ∥ L (\sum_{i = 1}^{m} (x_{i} - y_{i}) e_{i}) ∥ \\ \leq \sum_{i = 1}^{m} | x_{i} - y_{i} | ∥ L (e_{i}) ∥ \leq ∥ x - y ∥_{\infty} \sum_{i = 1}^{m} ∥ L (e_{i}) ∥ \end{aligned}$

So $L$ is a Lipschitz function, is uniformly continuous.
Norm $∥ \cdot ∥ : x \mapsto ∥ x ∥$ . $| ∥ x ∥ - ∥ y ∥ | \leq ∥ x - y ∥$ , Lipschitz.
The addition $R^{m} \times R^{m} \to R^{m}, (x, y) \mapsto x + y$ , number multiplication $R \times R^{m} \to R^{m}, (λ, x) \mapsto λ x$ and inner product $R^{m} \times R^{m} \to R, (x, y) \mapsto ⟨ x, y ⟩$ between vectors.
$f : E \to R, g : E \to R$ are continuous, then $f \cdot g : E \to R$ where $x \mapsto f (x) g (x)$ is also continuous.
$f : E \to R$ is continuous and $f (x_{0}) \neq 0$ , then $g : E \to R$ where $x \mapsto \frac{1}{f (x)}$ is also continuous.

Theorem 1.3.6 Assuming $f : E \to R^{p}$ is continuous at $x_{0} \in E$ and $g : E \to R^{q}$ is continuous at $f (x_{0}) = y_{0} \in F$ , then $g \circ f : (E \cap f^{- 1} (F)) \to R^{q}$ is continuous.

Theorem 1.3.7 Given $f : E \to R^{p}$ , $E \subseteq R^{m}$ ,

f(x1,...,xm ) = ∖left(∖right)

then $f$ is continuous at $x_{0} \in E \Leftrightarrow$ for any $k$ , $f_{k} : E \to R$ is continuous at $x_{0}$ .

Proof Hint. $\begin{array}{r} | f_{k} (x) - f_{k} (x_{0}) | \leq ∥ f_{k} (x) - f_{k} (x_{0}) ∥_{\infty} \leq \sum_{i = 1}^{p} | f_{i} (x) - f_{i} (x_{0}) | \end{array}$

$◻$

Example 1.3.2 If arbitrarily fixing one or more variable(s) will get a continuous function, does it mean the original function is continuous? No! See the example below.

Example 1.3.3 Is $f (x, y) = {\begin{cases} \frac{x y}{x^{2} + y^{2}} & (x, y) \neq (0, 0) \\ A & (x, y) = (0, 0) \end{cases}$ continuous?

Fix $y \neq 0$ , $f (x, y) = f_{y} (x) = \frac{x y}{x^{2} + y^{2}}$ is continuous with respect to $x$ . Fix $y = 0$ , $f (x, 0) = {\begin{cases} 0 & x \neq 0 \\ A & x = 0 \end{cases}$ , it’s continuous when $A = 0$ . Similar when fixing $x$ . So when $A = 0$ , fixing any variable will get a continuous function.

Now consider the continuity of binary $f (x, y)$ . When $(x_{0}, y_{0}) \neq (0, 0)$ , since $x_{0}^{2} + y_{0}^{2} > 0$ , according to the composition rule $f (x, y)$ is continuous.

Now consider $(x, y) = (0, 0)$ . Select a continuous curve $(x (t), y (t))$ with respect to $t$ and $lim_{t = 0} (x (t), y (t)) = (0, 0)$ , if $lim_{t = 0} f (x (t), y (t)) \neq A$ or even doesn’t exist, then $f$ is not continuous at $(x, y) = (0, 0)$ . Given $f (t, α t) = \frac{α}{1 + α^{2}}$ ; when $α = 0$ , $f (t, 0) = 0$ ; when $α = 1$ , $f (t, t) = \frac{1}{2}$ . $f (t \cos \frac{1}{t}, t \sin \frac{1}{t}) = \frac{1}{2} \sin \frac{2}{t}$ oscillates. So $f$ is not continuous whatever $A$ is.

Another example is $f (x, y) = {\begin{cases} \frac{x^{2} y}{x^{4} + y^{2}} & (x, y) \neq (0, 0) \\ 0 & (x, y) = (0, 0) \end{cases}$ . Even though $f (t, α t) = \frac{α t}{α^{2} + t^{2}} \to 0$ for any $α$ when $t \neq 0$ , we can select other strange curves $x (t), y (t)$ going to $(0, 0)$ yet $lim f (x (t), y (t))$ doesn’t exist.

Example 1.3.4 Application. Assuming a linear mapping $A : R^{n} \to R^{n}$ is symmetric, meaning for any $x, y$ , $⟨ A x, y ⟩ = ⟨ x, A y ⟩$ , prove that there exists a series of identity orthogonal bases $v_{1}, . . ., v_{n} \in R^{n}$ and a series of eigenvalues $λ_{1}, . . ., λ_{n}$ such that $A v_{k} = λ_{k} v_{k}$ .

Proof Let $K = {v \in R^{n} | ∥ v ∥ = 1}$ . $K$ is bounded ( $∥ v ∥ = 1$ ) and closed (the norm function is continuous). $f (v) = ⟨ A v, v ⟩$ is continuous with respect to $v$ , so $f$ has maximum point $v_{1}$ on $K$ . Arbitrarily select an identity vector $w ⊥ v_{1}$ , let $u (θ) = \cos θ v_{1} + \sin θ w \in K$ and $∥ u ∥ = \sqrt{⟨ u, u ⟩} = 1$ . So $\begin{aligned} f (u (θ)) & = ⟨ A (\cos θ v_{1} + \sin θ w), \cos θ v_{1} + \sin θ w ⟩ \\ = \cos^{2} θ ⟨ A v_{1}, v_{1} ⟩ + \sin^{2} θ ⟨ A w, w ⟩ + \cos θ \sin θ (⟨ A v_{1}, w ⟩ + ⟨ A w, v_{1} ⟩) \\ = (1 + o (θ)) ⟨ A v_{1}, v_{1} ⟩ + o (θ) ⟨ A w, w ⟩ + (θ + o (θ)) (⟨ A v_{1}, w ⟩ + ⟨ A w, v_{1} ⟩) \\ = g (θ) \end{aligned}$

$g (θ)$ is derivable and takes the maximum when $θ = 0$ , so $g^{'} (0) = 0 \to ⟨ A v_{1}, w ⟩ = 0$ , so $A v_{1}$ is perpendicular to all vectors which is perpendicular to $v_{1}$ , meaning that $A v_{1} ⊥ {v_{1}}^{⊥}$ , so there exists $λ_{1}$ such that $A v_{1} = λ_{1} v_{1}$ .

It is to be proved that $V_{1} = {v_{1}}^{⊥} = {w | w ⊥ v_{1}}$ is invariant under $A$ . For any $w \in V_{1}$ , $⟨ A w, v_{1} ⟩ = ⟨ w, A v_{1} ⟩ = ⟨ w, λ_{1} v_{1} ⟩ = 0$ , So $A V_{1} \subseteq V_{1}$ .

Then the spectral decomposition is proved by mathematical induction. $◻$