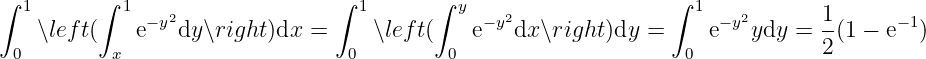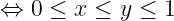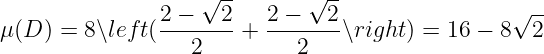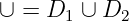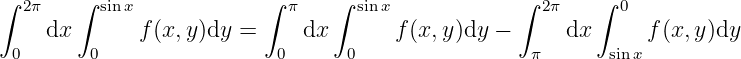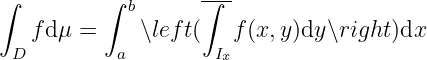The computation of multiple integral

4.2 The computation of multiple integral

Basic methods.

Decomposition of domain $D$ and function $f$ (linear combination, ...).
Transformation of variables to simplify either $D$ or $f$ .
Dimension/multiplicity reduction to one-variable integral or repeated integral.
Numerical. Approximate value and random process.

Repeated integral

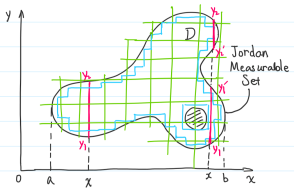
Definition 4.2.1 $D \subseteq R^{n}$ is a Jordan measurable set if $\forall ϵ > 0$ , $\exists$ finite rectangles $R_{1}, . . ., R_{N}$ such that $\partial D \subseteq R_{1} \cup \dots \cup R_{N}$ and $\sum_{k = 1}^{N} μ (R_{k}) < ϵ$ .

Assuming

\forall a \leq x \leq b

I_{x} = {y \in R^{n - 1} | (x, y) \in D}

. We consider the rectangle first. See Figure 4.1, we have

\begin{aligned} \int_{R} f d μ & = \int_{[a, b] \times [c, d]} f (x, y) d μ (x, y) = \sum_{k} f (ξ_{k}) | R_{k} | \\ = \sum_{i = 1}^{n} [\sum_{j = 1}^{n} f (x_{i}, y_{j}) Δ y_{j}] Δ x_{i} = \sum_{i = 1}^{n} \underset{g (x_{i})}{\underset{⏟}{\int_{c}^{d} f (x_{i}, y) d y}} Δ x_{i} \\ = \sum_{i = 1} g (x_{i}) Δ x_{i} = \int_{a}^{b} g (x) d x \end{aligned}

Therefore, we have

Theorem 4.2.2 (Fubini) If $D = R \subseteq R^{2}$ , $f \in R (D)$ , then

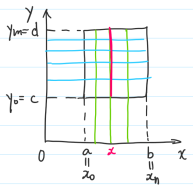
∫ ∫ ∫ ∫ ∫ b d d b fdμ = ∖lef t( f(x,y)dy ∖right)dx = ∖left( f (x,y)dx∖right )dy R a c c a

If $D$ is a Jordan measurable set, $f \in R (D)$ , $D \subseteq [a, b] \times R^{n - 1}$ , then $\forall x \in [a, b]$ , $\overset{―}{\int_{I_{x}}} f (x, y) d y$ exists, and

∫ ∫ ∫-- b fdμ = ∖left( f(x,y )dy ∖right)dx D a Ix

Example 4.2.1 Seek $\int_{0}^{1} (\int_{x}^{1} e^{- y^{2}} d y) d x = \int_{D} e^{- y^{2}} d μ$ . where $D = {(x, y) | 0 \leq x \leq 1, x \leq y \leq 1}$ .

Exchange the order of integral with assistance of graph. Transform $D$ into $D = {(x, y) | 0 \leq y \leq 1, 0 \leq x \leq y}$ , we have

∫ ∫ ∫ ∫ ∫ 1 1 −y2 1 y −y2 1 − y2 1- − 1 ∖left( e dy∖right)dx = ∖left( e dx∖right)dy = e ydy = 2 (1 − e ) 0 x 0 0 0

Exchange the order of integral without assistance of graph. Notice that

⇔ 0 ≤ x ≤ y ≤ 1

We have $\begin{aligned} \int_{0}^{1} (\int_{x}^{1} e^{- y^{2}} d y) d x = \int_{0}^{1} (\int_{- \infty}^{+ \infty} e^{- y^{2}} 1_{x \leq y \leq 1} d x) d y \\ = \int_{- \infty}^{+ \infty} (\int_{0}^{1} e^{- y^{2}} 1_{0 \leq y \leq 1} d x) d y = \int_{- \infty}^{+ \infty} (e^{- y^{2}} 1_{0 \leq y \leq 1} \int_{0}^{1} d x) d y \\ = \int_{0}^{1} e^{- y^{2}} y d y = \frac{1}{2} (1 - e^{- 1}) \end{aligned}$

Example 4.2.2 Assuming $D$ is the bounded closed set bounded with 3 cylindrical surface $x^{2} + y^{2} = 1, y^{2} + z^{2} = 1, z^{2} + x^{2} = 1$ . Seek its volume $μ (D)$ .

It is trivial that $D = {(x, y, z) | x^{2} + y^{2} \leq 1, y^{2} + z^{2} \leq 1, z^{2} + x^{2} \leq 1}$ , then we have $\begin{aligned} μ (D) & = \int_{D} 1 d μ = \int_{R^{3}} 1_{x^{2} + y^{2} \leq 1, y^{2} + z^{2} \leq 1, z^{2} + x^{2} \leq 1} d x d y d z \\ = \int_{- \infty}^{+ \infty} d x \int_{- \infty}^{+ \infty} d y \int_{- \infty}^{+ \infty} 1_{x^{2} + y^{2} \leq 1, y^{2} + z^{2} \leq 1, z^{2} + x^{2} \leq 1} d z \\ = \int_{- \infty}^{+ \infty} d x \int_{- \infty}^{+ \infty} d y \int_{| z | < min {\sqrt{1 - y^{2}}, \sqrt{1 - x^{2}}}} 1_{x^{2} + y^{2} \leq 1} d z \\ = 2 \int_{- \infty}^{+ \infty} \int_{- \infty}^{+ \infty} 1_{x^{2} + y^{2} \leq 1} min {\sqrt{1 - y^{2}}, \sqrt{1 - x^{2}}} d x d y \\ = 2 \int_{- \infty}^{+ \infty} d x \int_{- \infty}^{+ \infty} 1_{| y | \leq \sqrt{1 - x^{2}}} [\sqrt{1 - y^{2}} 1_{| y | \geq | x |} + \sqrt{1 - x^{2}} 1_{| y | < | x |}] d y \\ = 8 \int_{0}^{+ \infty} d x [\underset{I}{\underset{⏟}{\int_{0}^{+ \infty} 1_{0 \leq y \leq \sqrt{1 - x^{2}} \land y \geq x} \sqrt{1 - y^{2}} d y}} + \underset{II}{\underset{⏟}{\int_{0}^{+ \infty} 1_{0 \leq y \leq \sqrt{1 - x^{2}} \land y < x} \sqrt{1 - x^{2}} d y}}] \end{aligned}$

For I, we have $0 \leq x \leq y \leq \sqrt{1 - x^{2}} \Rightarrow 0 \leq x \leq \frac{\sqrt{2}}{2}$ , then

∫ √22 ∫ √1−x2∘ ------ ∫ √22- √ ------- √ -- I = dx 1 − y2dy = 1- ∖left(arcsin 1 − x2 − arcsin x∖right)dx = 2-−---2 0 x 2 0 2

For II, we have $y \leq min {x, \sqrt{1 - x^{2}}}$ , then $\begin{aligned} II & = \int_{0}^{1} \sqrt{1 - x^{2}} d x \int_{0}^{min {x, \sqrt{1 - x^{2}}}} d y = \int_{0}^{1} \sqrt{1 - x^{2}} min {x, \sqrt{1 - x^{2}}} d x \\ = \int_{0}^{\frac{\sqrt{2}}{2}} x \sqrt{1 - x^{2}} d x + \int_{\frac{\sqrt{2}}{2}}^{1} (1 - x^{2}) d x = \frac{4 - \sqrt{2}}{12} + \frac{8 - 5 \sqrt{2}}{12} = \frac{2 - \sqrt{2}}{2} \end{aligned}$

Terminally, we have

√ -- √ -- √ -- μ(D ) = 8∖left(2-−---2 + 2-−---2 ∖right) = 16 − 8 2 2 2

Example 4.2.3 Rewrite

1.: $\int_{D} f (x, y) d x d y ⟶ \int d y \int d x$ , $D = {(x, y) | x + y \leq 1, y - x \leq 1, y \geq 0}$ .
2.: $\int_{D} f (x, y) d x d y ⟶ \int d x \int d y$ , $D = {(x, y) | x + y \leq 1, y - x \leq 1, y \geq 0}$ .
3.: $\int_{D} | y - x^{2} | d x d y ⟶ \int d x \int d y, \int d y \int d x$ , $D = {(x, y) | | x | \leq 1, 0 \leq y \leq 2}$ .

Key.

1.: $\int_{D} f (x, y) d x d y = \int_{0}^{1} d y \int_{y - 1}^{1 - y} f (x, y) d x$ .
2.: $\int_{D} f (x, y) d x d y = \int_{- 1}^{1} d x \int_{0}^{1 - | x |} f (x, y) d y$ .
3.: $\int_{D} | y - x^{2} | d x d y = \int_{- 1}^{1} d x [\int_{0}^{x^{2}} (x^{2} - y) d y + \int_{x^{2}}^{2} (y - x^{2}) d x]$ ; $\begin{aligned} I & = \int_{D} | y - x^{2} | d x d y \\ = \int_{- \infty}^{+ \infty} d y \int_{- \infty}^{+ \infty} [(y - x^{2}) 1_{y \geq x^{2}} + (x^{2} - y) 1_{y < x^{2}}] 1_{- 1 \leq x \leq 1 \land 0 \leq y \leq 2} d x \\ = \int_{0}^{2} d y \int_{max {- 1, - \sqrt{y}}}^{min {1, \sqrt{y}}} (y - x^{2}) d x + \int_{0}^{1} d y \int_{- 1}^{- \sqrt{y}} (x^{2} - y) d x + \int_{0}^{1} d y \int_{\sqrt{y}}^{1} (x^{2} - y) d x \end{aligned}$

Example 4.2.4 Assuming $D_{1}, D_{2}$ are 2 bounded closed sets bounded with $z = x + 1, z = 0, x^{2} + y^{2} = 4$ . Seek $μ (D_{1}), μ (D_{2})$ .

Let $D = {(x, y) | z = x + 1, z = 0, x^{2} + y^{2} = 4} =$

∪ = D1 ∪ D2

For $D_{1}$ , we have $\begin{aligned} D_{1} & = \int_{x^{2} + y^{2} \leq 4} d x d y \int_{0}^{x + 1} d z = \int_{- 1}^{2} d x \int_{- \sqrt{4 - x^{2}}}^{\sqrt{4 - x^{2}}} d y \int_{0}^{x + 1} d z \\ = \int_{- 1}^{2} 2 (x + 1) \sqrt{4 - x^{2}} d x = 3 \sqrt{3} + \frac{8 π}{3} \end{aligned}$

Example 4.2.5 Exchange the order of the integral

∫ 2π ∫ sinx ∫ π ∫ sinx ∫ 2π ∫ 0 0 dx 0 f(x,y)dy = 0 dx 0 f (x,y)dy − π dx sinxf (x,y)dy