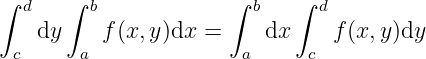3.1 Definite integral depending on a parameter
Definition 3.1.1
Assuming a function
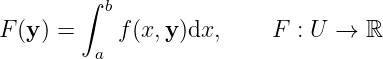
as the integral depending on a parameter, where
-
The limit/continuity of
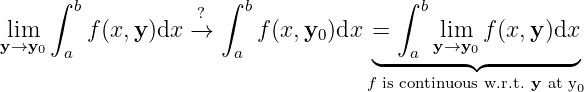
-
Derivability,
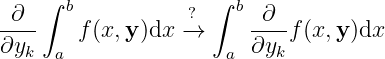
-
Integral.
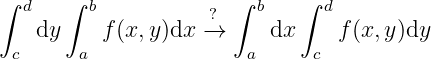
They are all questions like if the order of the original integral and some kind of the limit (i.e. limit, derivative and another integral) could be exchanged.
Limit. Assuming
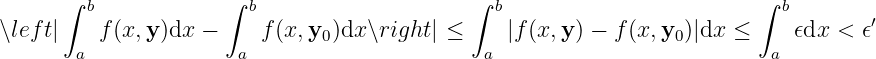
The proof above is wrong! Since
Theorem 3.1.2
Assuming
Then
Corollary 3.1.3
Assuming
Proof
If
Example 3.1.1 Define
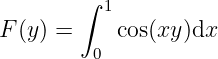
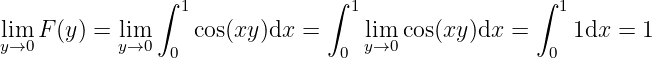
On the other hand, when
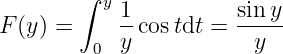
Derivability.
Theorem 3.1.5
Assuming
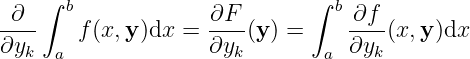
Proof
Only the last formula is needed to be proven. WLOG assuming
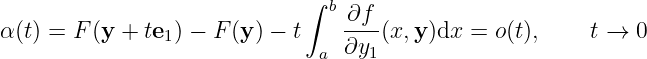
We have
The proof above is wrong! Since
Here

Hence, when
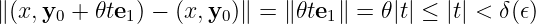
Therefore
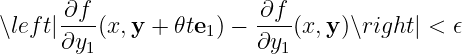
Terminally, theorem is proved.
Corollary 3.1.6
Assuming all
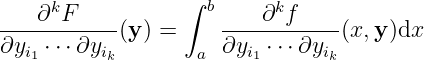
Integrability.
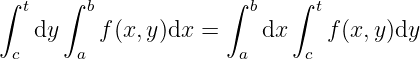
holds for any
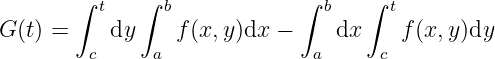
We have
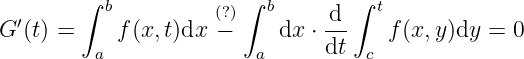
So
Why (?) is true? Assuming
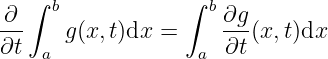
i.e.
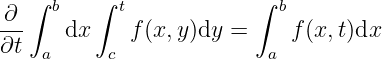
Example 3.1.2 When
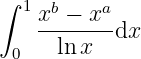
Assuming
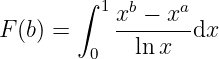
Consider
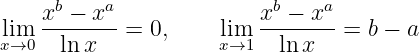
So we can define
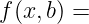
then
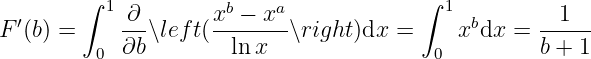
We can do the derivative since
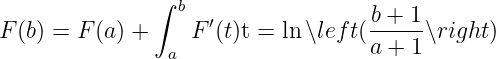
Example 3.1.3 (Variation) Assuming
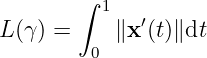
What’s
Let
![y (t,s) : [0,1] × [− δ,δ] → ℝn](main149x.png)
is of at least
Then we have
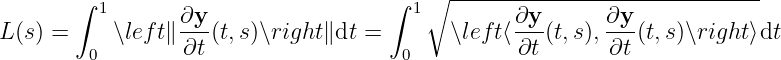
Assuming
Construct
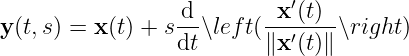
Therefore
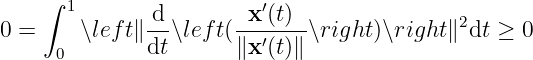
Since
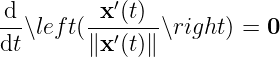
meaning
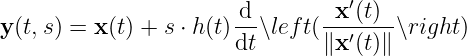
where
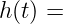
Therefore
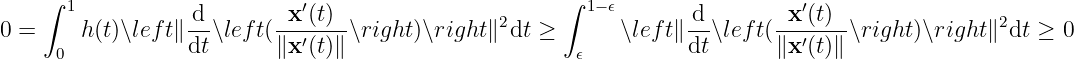
meaning
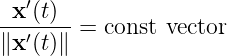
i.e.
Note: what we proved above is that if the curve of minimum length exists, then it can only be the straight line; yet we don’t prove that the curve of minimum length exists!
1When it comes to integral depending on a parameter, the condition