𝒪 and o

1.5 $O$ and $o$

Definition 1.5.1 $f = O (g)$ when $x \to a$ if there exists $M > 0$ and $δ_{0} > 0$ such that for any $0 < ∥ x - a ∥ < δ_{0}$ , $∥ f (x) ∥ \leq M ∥ g (x) ∥$ .

Definition 1.5.2 $f$ and $g$ has the same order when $x \to a$ if and only if $f = O (g)$ and $g = O (f)$ , meaning there exists $M > 0$ and $δ_{0} > 0$ such that for any $0 < ∥ x - a ∥ < δ_{0}$ , $\frac{1}{M} ∥ g (x) ∥ \leq ∥ f (x) ∥ \leq M ∥ g (x) ∥$ .

Definition 1.5.3 $f = o (g)$ when $x \to a$ if for any $ϵ > 0$ , there exists $δ_{ϵ} > 0$ such that for any $0 < ∥ x - a ∥ < δ_{0}$ , $∥ f (x) ∥ \leq ϵ ∥ g (x) ∥$ .

Definition 1.5.4 $f$ and $g$ are equivalent if and only if $f = g + o (g)$ .

Theorem 1.5.5 Given $f, g : E \to R^{p}$ , where $\begin{aligned} f (x) & = {(\begin{array}{c} f_{1} (x) & \dots & f_{p} (x) \end{array})}^{T} \\ g (x) & = {(\begin{array}{c} g_{1} (x) & \dots & g_{p} (x) \end{array})}^{T} \end{aligned}$

then $f = O (g) \Leftrightarrow f_{k} = O (g_{k})$ , for any $k$ .

Proof Hint.

1 1 ---|fk(x)| < ---∥f(x )∥ ∞ ≤ ∥f (x)∥ ≤ M ∥f(x)∥1 = M ∖lef t[|f1(x)| + ...+ |fp(x)|∖right ] M M

$◻$

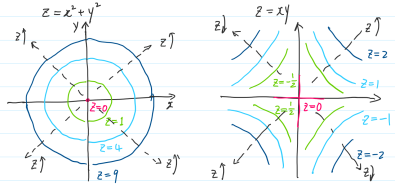
Example 1.5.1 Several examples for $O$ and $o$ .

1.: Linear (matrix) $A$ . $A x = O (x)$ , since $∥ A x ∥ \leq ∥ A ∥ ∥ x ∥$ .
2.: Quadratic form. $⟨ A x, x ⟩ = O (∥ x ∥^{2})$ , since $| ⟨ A x, x ⟩ | \leq ∥ A x ∥ ∥ x ∥ \leq ∥ A ∥ ∥ x ∥^{2}$ .
3.: $x y = O (x^{2} + y^{2}), (x, y) \to (0, 0)$ , since $| x y | \leq \frac{x^{2} + y^{2}}{2}$ . Does $x y$ has the same order as $x^{2} + y^{2}$ when $(x, y) \to (0, 0)$ ? No! For any $δ$ -deleted neighborhood of $(0, 0)$ , there exists a point whose components $x \neq 0$ and $y = 0$ . Here $0 < ∥ (x, 0) - (0, 0) ∥_{2} = | x | < δ$ . If $x^{2} + y^{2} = O (x y)$ , then there exists $M, δ_{1} > 0$ such that for any $(x, 0)$ , $0 < ∥ (x, y) - (0, 0) ∥ < δ_{1}$ , $x^{2} + y^{2} \leq M | x y |$ , here $0 < x^{2} \leq M | x \cdot 0 | = 0$ , contradicted.
4.: $x^{2} + y^{2}$ has the same order as $2 x^{2} + 3 y^{2}$ , since $2 (x^{2} + y^{2}) \leq 2 x^{2} + 3 y^{2} \leq 3 (x^{2} + y^{2})$ .
5.: The difference between $x y$ and $x^{2} + y^{2}$ is shown in Figure 1.1. They don’t have the same order because their graph near $(0, 0)$ is different. Therefore, the definition of an exact order on the textbook is not well-defined, because the relation between $x, y$ may result in various results.

1.5 O and o

1.5 $O$ and $o$