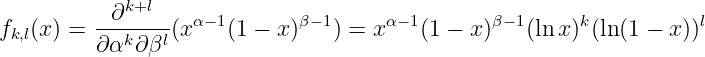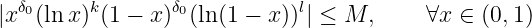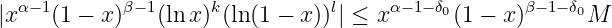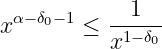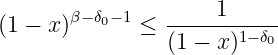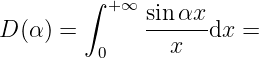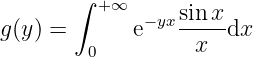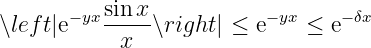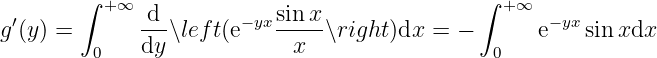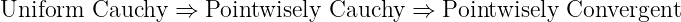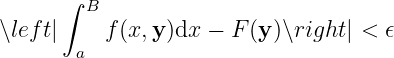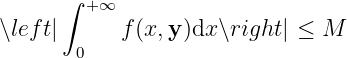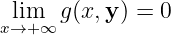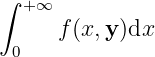Proof
, obviously. , we have
So , , such that ,
Therefore, , we have
Example 3.3.1 Gamma function
is of with respect to .
Let , then
If is uniformly convergent with respect to in a certain neighborhood , then
We use a strong Weierstrass function (with no respect to ) to control the integrand. Consider
-
Take any , it could be proved by L’Hôpital that
So is bounded on , meaning such that . Hence, for ,
According to Weierstrass Criterion, I is uniformly convergent for .
-
Take any , for ,
According to Weierstrass Criterion, II is uniformly convergent for .
Therefore, is uniformly convergent with respect to , meaning is -order derivable in .
Example 3.3.2 Beta function .
is of with respect to and
When ,
Let
We need to prove that is uniformly convergent with respect to in any bounded closed set of
.
Take any , , such that
Therefore,
According to Weierstrass Criterion, is uniformly convergent with respect to , meaning is -order
derivable with respect to and -order derivable with respect to in .
Prove the relation between Gamma function and Beta function.
Example 3.3.3 Dirichlet function .
Let
Take any , then for any , we have
convergent. According to Weierstrass Criterion, is uniformly convergent with respect to
.
is uniformly consistent with respect to , meaning is derivable in .
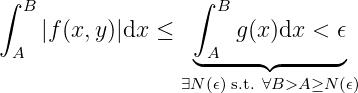
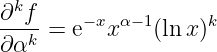
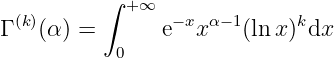
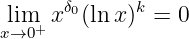
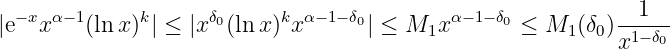
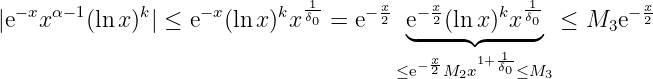
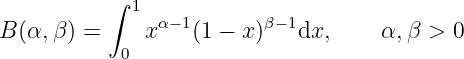
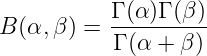
![( )
Γ (m-+-n)- (m--−-1)!(n-−-1)! m + n − 2 − 1
B (m, n) = Γ (m )Γ (n) = (m + n − 1)! = ∖left[ m − 1 (m + n − 1 )∖right ]](main187x.png)