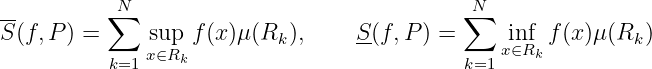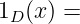4.1 The concept of multiple integral
is a bounded closed set, ,
is the multiple integral where is the -dimension volume infinitesimal at .
Recall: Riemann integral of 1-dimension.
Definition 4.1.1
Riemann sum. Given a partition of :
and a set of symbol points , then
, such that a partition ,
Then is Riemann integrable on .
Definition 4.1.2
Darboux. Assuming is
bounded,
given a partition , let
If is more dense, then decreases and increases. If , a partition such that
Then is Darboux integrable on .
Theorem 4.1.3
The following 3 statements are equivalent.
-
1.
-
(Riemann) is Riemann integrable on .
-
2.
-
(Darboux) is Darboux integrable on .
-
3.
-
(Lebesgue) is bounded, and is a set of measure .
Definition 4.1.4
is a set of measure if , countable intervals such that and .
Corollary 4.1.5
All continuous functions on are integrable. All monotonous functions on
are integrable.
Rectangle in .
Definition 4.1.6
Assuming
then is called the -dimension volume of .
Definition 4.1.7
are the partition of the rectangle if
- where are all rectangles.
- , .
Definition 4.1.8
Riemann sum in higher dimension.
is Riemann integrable on rectangle if such that , such that for any partition of ,
Mark
as the Riemann integral of on . When the dimension , it’s also called the multiple integral.
Definition 4.1.9
Darboux.
is Darboux integral on rectangle if
Theorem 4.1.10
The following 3 statements are equivalent for any function defined on rectangle
.
-
1.
-
(Riemann) is Riemann integrable on .
-
2.
-
(Darboux) is Darboux integrable on .
-
3.
-
(Lebesgue) is bounded, and is a set of measure .
Corollary 4.1.11
All continuous functions on bounded closed rectangle are integrable.
Assuming is a bounded closed set of any shape, , how to seek ?
Thus, we have
Definition 4.1.12
Assuming is a bounded closed set where is a set of measure , . Let
rectangle satisfy , construct
If is integrable on , then is integrable on , and
Corollary 4.1.13
If is bounded closed where is a set of measure , then all continuous
functions on is integrable.
Corollary 4.1.14
Indicator function
is Riemann integrable on , define .
-
1.
-
Linearity. is a linear space, is linear, i.e. , , and
-
2.
-
Isotonicity. and , then
-
3.
-
Triangle inequality. , and , so
-
4.
-
Cauchy-Schwartz inequality. , then
-
5.
-
Integral mean theorem. Assuming is (path-)connected, and , , then , such that
When the denominator is non-zero, we have
It is a weighted mean of where is the weight.
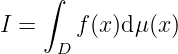
![∫ b ∫
I = a f(x )dx = [a,b]f(x)dx](main213x.png)
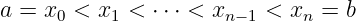
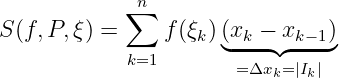
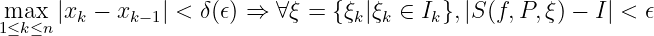
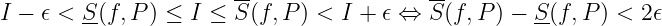
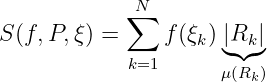
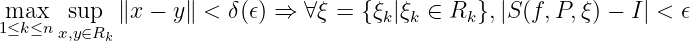
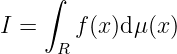
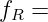
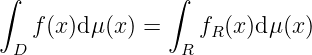
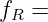
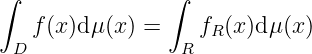
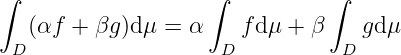
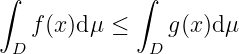
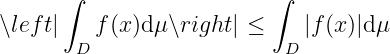
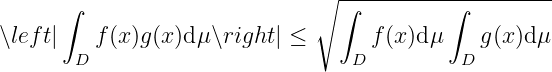
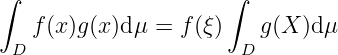
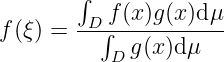
![n
R = [a1,b1] × [an,bn] = {x = (x1,...,xn ) ∈ ℝ |ai ≤ xi ≤ bi,i = 1,...,n}](main218x.png)