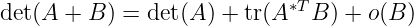2.1 Derivative of multiple variable function
In single variable function, the derivative of
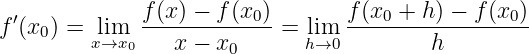
In multiple variable function, since one could not be divided by a vector, so we should rewrite the
expression above.
Definition 2.1.1
Definition 2.1.2
Note In 1-dimension case, the derivative
When
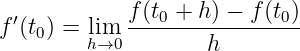
If regard
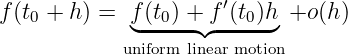
is the best uniform linear motion to approximately describe the original real motion. Here
Definition 2.1.3
Given
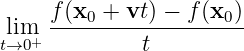
exists, then it’s marked as
Note
- Notice that
-
Mark
Therefore for any
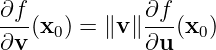
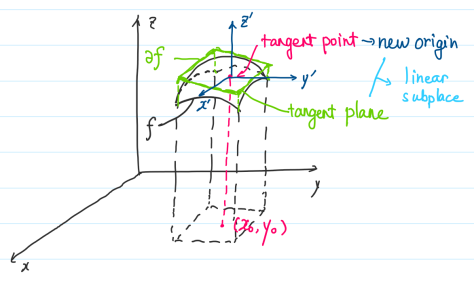
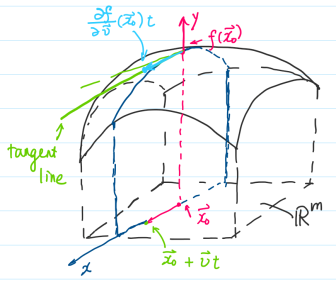
- The geometric meaning of directional derivative is shown in Figure 2.2. The slope of the green
tangent line in
- If
- 1.
-
If
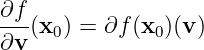
- 2.
-
When
Example 2.1.1 Several examples for derivable functions.
- 1.
-
Constant mapping.
- 2.
-
Linear mapping.
- 3.
-
Inner product. Given a linear mapping
- 4.
-
Consider
Therefore
when
Consider invertible
Therefore
- 5.
-
If
Therefore
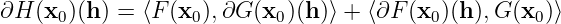
- 6.
-
Consider
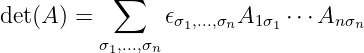
where
Consider a special matrix
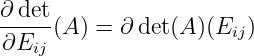
we have
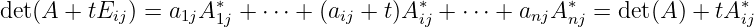
i.e.
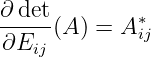
Therefore
Terminally