4.3 习题课讲解
4.3.1 隐函数定理
例 4.3.1 ( )
函数由方程确定,求的导函数。
)
函数由方程确定,求的导函数。
解
将函数代入方程得到恒等式
是保证隐函数存在的充分条件。
采用全微分的过程与上面类似。
例 4.3.2 (例1)
已知函数由方程确定,其中 是常数,求的导函数。
解1
方程两边对求导,可得
解得
解2
对
用隐函数定理结论,可得
注
千万别把偏导数当成分数,从而得到这样的错误结论。
例 4.3.3 (例2)
设,证明:方程所确定的隐函数满足
证明1
记、,则有
两边对求偏导,可得
亦即
解得
同理解得
代入验证即可得到。
证明2
记,则方程确定隐函数。计算可得
由隐函数定理可得
所以
例 4.3.4 (例3, )
方程组
何时可以确定可微的隐函数 ?对隐函数计算。
)
方程组
何时可以确定可微的隐函数 ?对隐函数计算。
解1
先求导,再解方程。将方程对求导数,得到Jacobi矩阵
当时,可逆。此时由隐函数定理,方程组确定唯一的可微的隐函数 。两边求微分得
解得
亦即、。继续计算可得
当时,由方程组解得。此时都不是的函数,不存在隐函数。
解2
先解方程,再求导。方程解得,根据特解情况,分别对应四组隐函数
求导得到、,从而当 时,、。这告诉我们,方程易解时,不必使用隐函数定理或反函数定理。
解3
隐函数定理和逆映射定理是在方程无法简单求解时,用来确保解的存在性、唯一性和可微性,以及如何通过计算导数得到解的近似展开。
注
已知,而!实际上应该写作,故有
例 4.3.5 (例4, )
已知函数由参数方程
给定,试求。
)
已知函数由参数方程
给定,试求。
解1
两边求微分,得到
由前两个方程解得
根据逆映射定理,是存在可微逆映射的充分条件。代入第三式,得到
所以
同样,我们可以求二阶偏导:
解2
方程解得、、。计算可得
注
,则有,而!应当使用矩阵求逆计算,即
例 4.3.6 (例5, )
设,试给一个充分条件,使得由方程
可确定可微的隐函数,并求。
)
设,试给一个充分条件,使得由方程
可确定可微的隐函数,并求。
解
从
解得当 时,由
代入可得
所以
这些结果可以先用量纲检查。
注1
所有结果都要用来表示。本题实际上需要找到,因此充分条件为。时刻注意:隐函数定理需要验证的是对因变量的Jacobi矩阵可逆!
注2
五个变量满足的三个方程为什么能或怎样确定二元函数 ?事实上,由后两个方程
只要可逆,就可由隐函数定理得到可微的隐函数,再将它们代入第一个方程就得到。也可以这样解释:由最后一个方程可得隐函数或,代入第二个方程,只要这个复合函数关于变量的偏导数非零,即可解得,从而,再代入第一个方程就得到。
注3
如果不指明,有意义吗?按隐函数定理,五个自变量,三个方程的方程组,通常会确定三个变量为其余两个自变量的函数。而确认了是因变量(函数值),是自变量,而剩余的中会有一个为自变量,而剩下的两个是因变量(函数值)。如果不是问题中出现了二阶偏导数,指明了是自变量,从而是因变量,那么仅靠是无法确认变量之间的函数关系的,也就是说会有歧义。
为了避免这种歧义,物理学家发明了一个很好的符号,,它表示当作为自变量的二元函数时,固定不变,对求的偏导数。感兴趣的读者可以算一算。
注4
由此我们知道函数的偏导数是与空间的坐标系有关的。而函数的微分(由于链式法则)具有形式不变性,也就是说它不依赖与空间坐标系。所以学会使用微分进行计算是有好处的。我们在上面两个例子中都示范了用微分来做计算。
例 4.3.7 ( )
设可微,满足
证明:对任意,存在它的一个邻域,方程
唯一确定了三个可微函数,且满足
)
设可微,满足
证明:对任意,存在它的一个邻域,方程
唯一确定了三个可微函数,且满足

图 4.3.1: 奶酪越多,奶酪就越少
证明
由于可微且,由隐函数定理知方程唯一确定了三个可微函数,且满足
因此
4.3.2 隐函数定理的几何应用
例 4.3.8 (例6)
求曲面上切平面与直线平行的切点的轨迹。
解
与曲面在点处的切平面平行,所以曲面的法向量与直线垂直。直线的两个法向量为 和 ,所以
即,从而所求轨迹为曲面上的曲线为
例 4.3.9 (例7)
证明球面与锥面正交。
证明
所谓两曲面正交是指它们在交点处的法向量互相垂直。记、,曲面和曲面在其交点处的法向量分别是
它们的内积为
因此两曲面正交。
例 4.3.10 (例8)
过直线作曲面的切平面,求该切平面的方程。
解
设曲面在点处的切平面
即。直线 在该平面上,当且仅当
有无穷多解,从前两个方程解得,代入第三个方程得到
对所有成立,因此的系数上述方程曲面方程
相应的切平面方程为和。
例 4.3.11 (例9)
通过曲面上点的切平面____。
-
(A)
-
通过轴;
-
(B)
-
平行于轴;
-
(C)
-
垂直于轴;
-
(D)
-
以上都不对。
解
选B。设,代入曲面方程得到
在处Taylor展开并忽略高阶项,得到,从而所求切平面为。
例 4.3.12 (例10)
已知可微,证明:曲面上任意一点处的切平面通过一定点,并求此点位置。
证明
任取曲面上一点,过点和点的直线都在这个曲面上,所以点处的切平面都过点。曲面是以为顶点的一个锥面。
例 4.3.13 (例11)
曲面由方程确定,试证明:曲面上任一点的法线与某定直线相交。
证明
曲面上任意一点的法线为
取,则。所以所有法线都与直线相交。
例 4.3.14 (例12)
在椭球面上求一点,使椭球面在此点的法线与三个坐标轴的正向成等角。
解
椭球面在此点的法向量
与平行,所以,代入曲面方程可得
解得
例 4.3.15 (例13,Mercator地图, )
从球面的球心引射线,把球面上除南北两极以外的点映射到圆柱面上的点。
)
从球面的球心引射线,把球面上除南北两极以外的点映射到圆柱面上的点。
-
(1)
-
请写出关于的表达式。
-
(2)
-
如果球面上的点用经度和地理维度刻画,圆柱面上的点用经度和高度刻画,请写出的表达式。
-
(3)
-
求一元函数,使得映射,是一个保角变换,即球面上任何两条相交曲线的夹角(即曲面切线的夹角)等于这两条曲线在柱面上对应曲线的夹角。
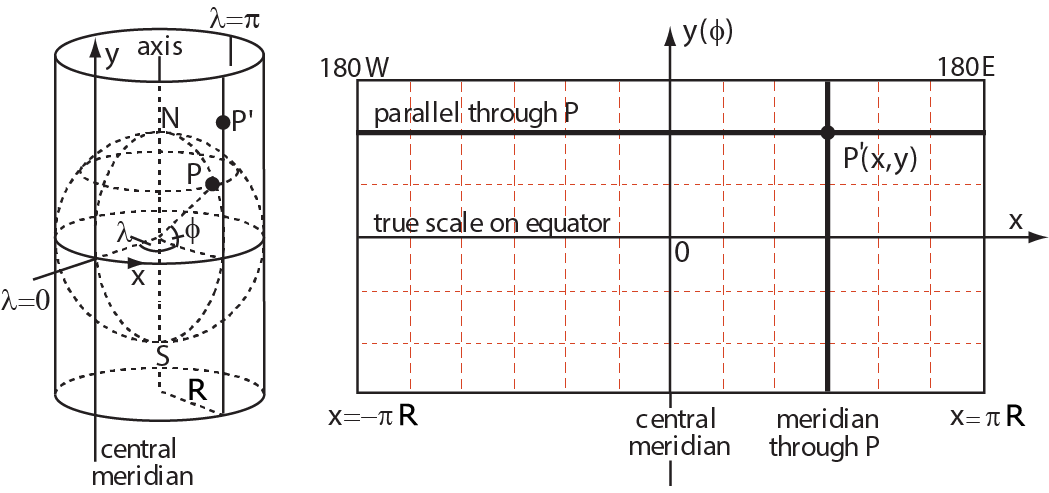
图 4.3.2: Mercator地图
解
(1) 设,则
因此
(2) 由题可得,故
(3) 设是球面上过点的一条光滑曲线,则把映为柱面上过点的一条光滑曲线
设、,计算可知的速度向量为
球面上处的两个切向量的内积为
夹角的余弦为
上相应的速度向量为
柱面上处的两个切向量的内积为
夹角的余弦为
由题可知对任意均成立,当且仅当
因此
在实际使用中考虑到对称性等因素,我们选择。
将球面上的所有点通过映射到柱面上,沿柱面的母线剪开就得到一张地图,这就是Mercator地图。我们实际上证明了:Mercator地图上所画的两条相交道路的夹角与实际道路的夹角大小相等。
另解
(3) 设曲线在处的速度向量为。构造如下映射:
故有
由于为球面或柱面的正交参数化,故可设方向的单位向量分别为,定义曲线的倾角满足下列方程的唯一解:
容易验证有下式成立
因此我们只需要证明保倾角即可证明保角。
保倾角的必要条件为保其正切值。注意到
则有
故有
因此
亦即
为了保倾角,应选择正号;考虑到对称性,应选择。故。
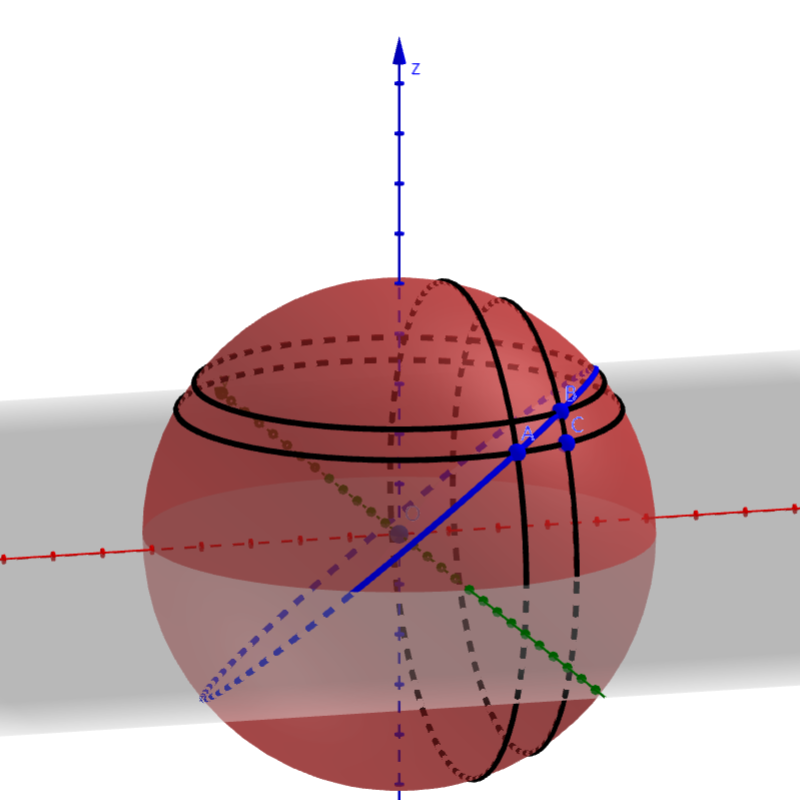
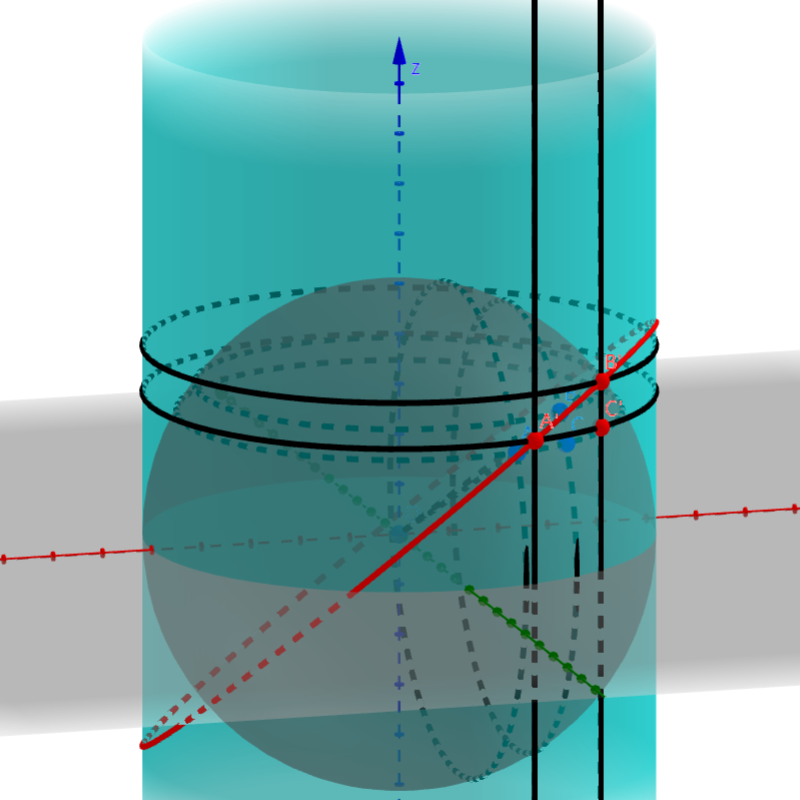
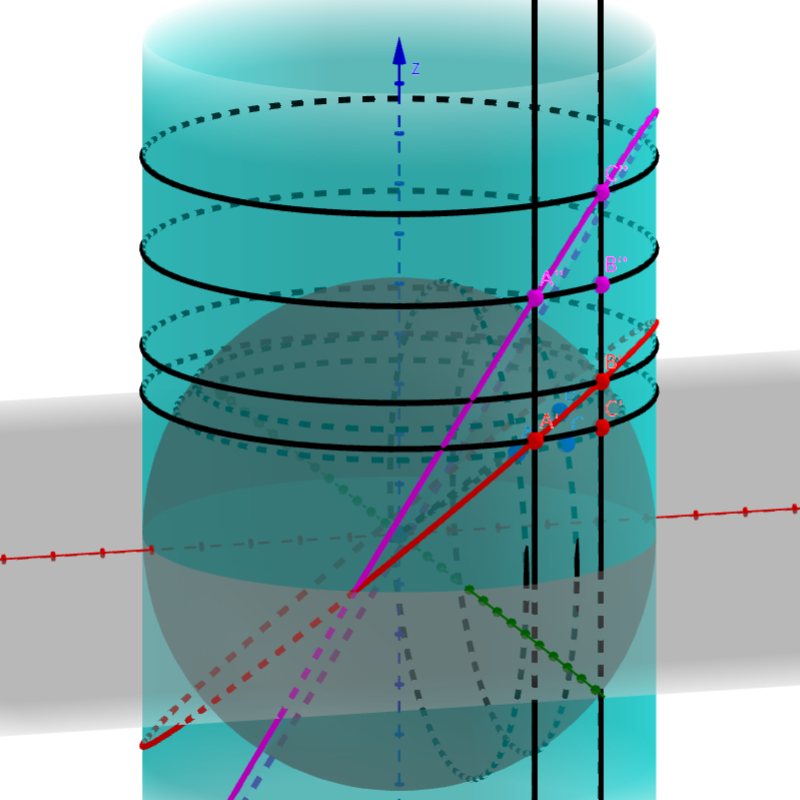
图 4.3.3: Mercator地图
4.3.3 与隐函数定理有关的证明题
例 4.3.16 ( )
设是矩阵的一个单重特征值(即,,其中),是对应于的一个单位特征向量。证明:存在,使得对任意矩阵,只要,就有唯一的特征值和相应的单位特征向量使得、,并且和关于是的。
)
设是矩阵的一个单重特征值(即,,其中),是对应于的一个单位特征向量。证明:存在,使得对任意矩阵,只要,就有唯一的特征值和相应的单位特征向量使得、,并且和关于是的。
证明
构造方程
则映射在处对的Jacobi矩阵为
故有
记,则有
设,则。对任意且,注意到的代数重数为1,则
因此,,即可逆。由隐函数定理可知存在,使得对任意,存在唯一的和分别为的特征值和相应的特征向量。由于是的,故和关于也是的。
注1
如果不是的单重特征值,上面的结论还成立吗?
从证明中不难看出,如果的代数重数不为1,即便其几何重数为1(见注2),仍有不可逆,亦即不可逆,故隐函数定理不适用。我们可以举一个反例:
显然特征向量的方向是不确定的,我们可以选择合适的使其朝向任意方向。
如果仅仅考虑特征值,则本题会更加简单:构造函数,隐函数定理适用的充分条件是,即是的单重特征值。
注2
设为阶方阵的特征值,几何重数,则其特征子空间中存在垂直于的非零向量使得,此时,故不可逆。
设为阶方阵的特征值,代数重数、几何重数,相应的特征向量为。设是的所有单位特征向量,相应的特征值为,,补充单位正交基。由于的几何重数为1,故。
设在单位正交基上的表示矩阵为
假设的所有特征值都不等于,则
此时的代数重数为1,与题设矛盾!故至少有一个特征值等于。
设的特征值对应的特征向量为,则对于向量,设
选择使得
故需满足
因此不可逆,故隐函数定理不适用。
例 4.3.17 ( )
设函数可微,为光滑曲面(即连续可微、梯度处处不为)在点处的切平面,为切平面上任意一条过点的直线,求证:在曲面上存在一条曲线,该曲线在点处的切线恰好为。
)
设函数可微,为光滑曲面(即连续可微、梯度处处不为)在点处的切平面,为切平面上任意一条过点的直线,求证:在曲面上存在一条曲线,该曲线在点处的切线恰好为。
证明
本题的关键在于把曲线(隐式地)构造出来。记为在处的法向量,为的方向向量,显然。令,构造过点、以为法向量的平面,令为曲面与平面的交线。下面我们依次证明:(1) 在的邻域存在;(2)
在处的切线就是,亦即在处的切向量平行于。
(1) 将写成隐函数的形式:
计算可得Jacobi矩阵为
由于,故必存在可逆使得的邻域内存在隐函数,亦即存在,其中。
(2) 由隐函数定理可得
因此
其中为Levi-Civita记号(全反对称张量,此处取值为),即在处的切向量平行于。
4.3.4 杂题
例 4.3.18 ( )
求下面方程的通解:
)
求下面方程的通解:
解
特征方程组为
亦即
解得特征线为
设,则原方程的通解为

 )
从球面
)
从球面


