3.1 第2次作业评讲
3.1.1 概念和计算部分
例 3.1.1
判断题:
-
(1)
-
( 74%)一元函数在一点处的左导数就是这个函数沿数轴向左的方向导数。
74%)一元函数在一点处的左导数就是这个函数沿数轴向左的方向导数。
-
(2)
-
( 58%)一个函数沿坐标轴方向的方向导数就是该函数对这个坐标求的偏导数。
58%)一个函数沿坐标轴方向的方向导数就是该函数对这个坐标求的偏导数。
-
(3)
-
( 51%)一个可微函数在一点处所有偏导数组成的向量就是这个函数在该点处的梯度向量。
51%)一个可微函数在一点处所有偏导数组成的向量就是这个函数在该点处的梯度向量。
解
(1) 错。左导数的定义为
方向导数的定义为
(2) 错。如果这个坐标轴上的基底向量不是单位向量,那么偏导数就不是方向导数。
(3) 错。如果自变量空间中没有内积,那么仍然可以定义函数的微分和偏导数,但是不能定义梯度;当自变量空间中有内积时,只有坐标系对应的基底向量是该内积下的一组单位正交基底向量,这个说法才是对的。
例 3.1.2
不定项选择题:
-
(4)
-
( 68%)函数
在原点处
68%)函数
在原点处
-
(A)
-
连续
-
(B)
-
存在偏导数
-
(C)
-
偏导数连续
-
(D)
-
可微
-
(5)
-
( 56%)函数
在原点处
56%)函数
在原点处
-
(A)
-
连续
-
(B)
-
存在偏导数
-
(C)
-
偏导数连续
-
(D)
-
可微
-
(6)
-
( 54%)函数
在原点处
54%)函数
在原点处
-
(A)
-
连续
-
(B)
-
沿所有方向都有方向导数
-
(C)
-
沿某些方向有方向导数,但沿另一些方向没有方向导数
-
(D)
-
可微
解
(4) AB。由于,,故在连续。计算可得
故在处不连续。同理亦在处不连续,故在处不存在偏导数。
注意到,故沿向量的导数为。由于,而
故在处不可微。
(5) ABD。由于,故连续、可微、偏导数存在。计算可得
然而
故在处不连续。同理亦在处不连续,故在处偏导数不连续。
(6) B。由于,故不连续,自然不可微。设,计算可得
故在处沿所有方向都有方向导数。
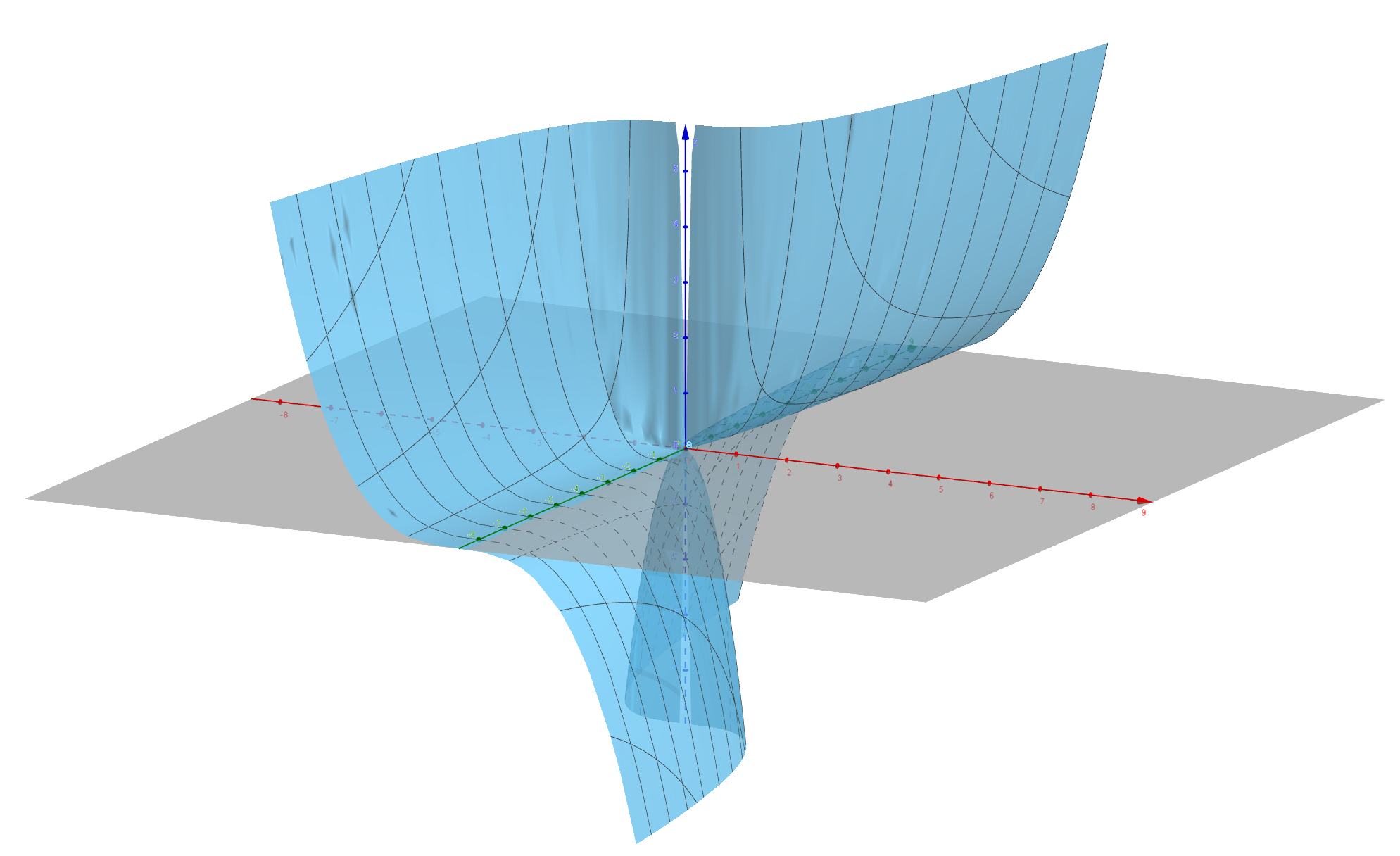
图 3.1.1: 函数的图像
例 3.1.3
填空题:
-
(7)
-
( 67%)已知是上的可微函数,满足
记,则等高线在点处的切线方程为____。
67%)已知是上的可微函数,满足
记,则等高线在点处的切线方程为____。
解
计算可知
代入可得
根据可微(切空间)的定义可得切线方程为
3.1.2 解答和证明部分
例 3.1.4 (解答题1,
 ,
, 79%)
用偏导数判别函数连续性和可微性。设二元函数在处存在偏导数,在的邻域内存在偏导数。证明:
79%)
用偏导数判别函数连续性和可微性。设二元函数在处存在偏导数,在的邻域内存在偏导数。证明:
-
(1)
-
如果偏导数有界,则在处连续;
-
(2)
-
如果偏导数连续,则在处可微。
证明
(1) 由题知
类似例2.3.22,仍然借助为媒介,考虑 由Lagrange中值定理可得
由Lagrange中值定理可得 由在处关于的偏导数存在,可知其关于一元连续,故
由在处关于的偏导数存在,可知其关于一元连续,故 故,,使得
即在处连续。
故,,使得
即在处连续。
(2) 参见例2.3.22,以为媒介 、方向使用偏导数定义
、方向使用偏导数定义 、方向使用Lagrange中值定理
、方向使用Lagrange中值定理 ,可得在处可微。
,可得在处可微。
注
大家在使用大O、小o记号时一定要注意:确保你的记号与其他变量无关!不然,我们可以这么“证明”若分别关于和连续,则关于二元连续:
我推荐大家采用这种写法,强调这里关于的小o可能与有关。
例 3.1.5 (解答题2,
 ,
, 86%)
设是可微函数,证明:
86%)
设是可微函数,证明:
-
(1)
-
如果是常数,且满足恒等式,则对于任意,直线是的等高线。
-
(2)
-
如果满足恒等式,则是零次齐次函数,即对任意以及,。
-
(3)
-
对正整数,证明是次齐次函数当且仅当,即对任意 以及,。
证明
(1) 将直线改写为参数方程
构造函数,求导可得
故亦即直线是的等高线。
(2) 设,构造函数,求导可得
故,即是零次齐次函数。
(3) :设,构造函数,求导可得
故,即是次齐次函数。
:等式两边对求导可得
令即可。
另证(3)
设,构造函数,求导可得
由此解得
注1
本题(3)问的难点在于如何理解,它的意思是:
注2
本题(1)问是验证直线为的等高线。若是证明的等高线是直线,即求出方程的解,难度更大。求解一阶线性偏微分方程有专门的方法,称为特征线法,参见第4.2.8节。对于本题而言,特征线为
作换元,计算可得
代入原式可得
所以即为的等高线。这实际上是原一阶线性偏微分方程的首次积分。
例 3.1.6 (解答题3,
 ,
, 87%)
设函数是具有连续二阶偏导数。已知变换:
87%)
设函数是具有连续二阶偏导数。已知变换:
-
(1)
-
把微分方程改写为关于函数的偏微分方程。
-
(2)
-
求上述微分方程的解。
-
(3)
-
【本问不计分】为什么要做上面这样的坐标变换?
解
(1) 计算可得 首先作因变量换元,计算可得
再作自变量换元,计算可得
首先作因变量换元,计算可得
再作自变量换元,计算可得
(2) 换元后的方程相当于关于的常微分方程,但要注意任意常数可以与有关 ,解得
,解得 代入,将并入,得
其中。
代入,将并入,得
其中。
(3) 这是一个二阶线性偏微分方程,换元法是为了将其化为标准形,参见第4.2.9节。关注二阶项的系数,判别式,故这是一个抛物型方程,其特征线为
由此解得唯一一个首次积分。任选与此无关的变量(如)构成换元,使得原方程化为抛物型方程的标准式。
例 3.1.7 (解答题4,
 ,
, 92%)
设 是平面直角坐标系中的一个二阶连续可微函数,是平面极坐标。
92%)
设 是平面直角坐标系中的一个二阶连续可微函数,是平面极坐标。
-
(1)
-
求偏导数和,并判断它们是否为函数的方向导数,解释你的结论。
-
(2)
-
求函数在极坐标系下的梯度。
-
(3)
-
证明。你能给这个等式一个直观解释吗?
-
(4)
-
把表达式用极坐标下的偏导数表达。
解
(1) 计算可得 故可视作沿半径方向的方向导数
故可视作沿半径方向的方向导数 ;但由于的存在,不是沿角度方向的方向导数
;但由于的存在,不是沿角度方向的方向导数 。
。
(2) 梯度与方向导数的关系为
分别取和,则
由于,故
(3) 容易发现 这个等式的直观解释就是梯度与具体的坐标系无关。
这个等式的直观解释就是梯度与具体的坐标系无关。
(4) 计算可得
继续计算可得
对于,将上式中的换为即可,亦即
两者相加可得
注
第(4)问不要想当然地认为
原因在于求偏导和乘法不可交换,是个形式记号,是右边的矩阵系数直接乘在偏导算子的左边,而不是偏导算子作用在右边的矩阵上。
 74%)一元函数在一点处的左导数就是这个函数沿数轴向左的方向导数。
74%)一元函数在一点处的左导数就是这个函数沿数轴向左的方向导数。
 58%)一个函数沿坐标轴方向的方向导数就是该函数对这个坐标求的偏导数。
58%)一个函数沿坐标轴方向的方向导数就是该函数对这个坐标求的偏导数。
 51%)一个可微函数在一点处所有偏导数组成的向量就是这个函数在该点处的梯度向量。
51%)一个可微函数在一点处所有偏导数组成的向量就是这个函数在该点处的梯度向量。 68%)函数
68%)函数 56%)函数
56%)函数 54%)函数
54%)函数

 ,
, 79%)
用偏导数判别函数连续性和可微性。设二元函数
79%)
用偏导数判别函数连续性和可微性。设二元函数


 、
、 、
、 ,可得
,可得
 ,
, 86%)
设
86%)
设




 ,
, 87%)
设函数
87%)
设函数
 ,解得
,解得

 ,
, 92%)
设
92%)
设 
 ;但由于
;但由于 。
。


