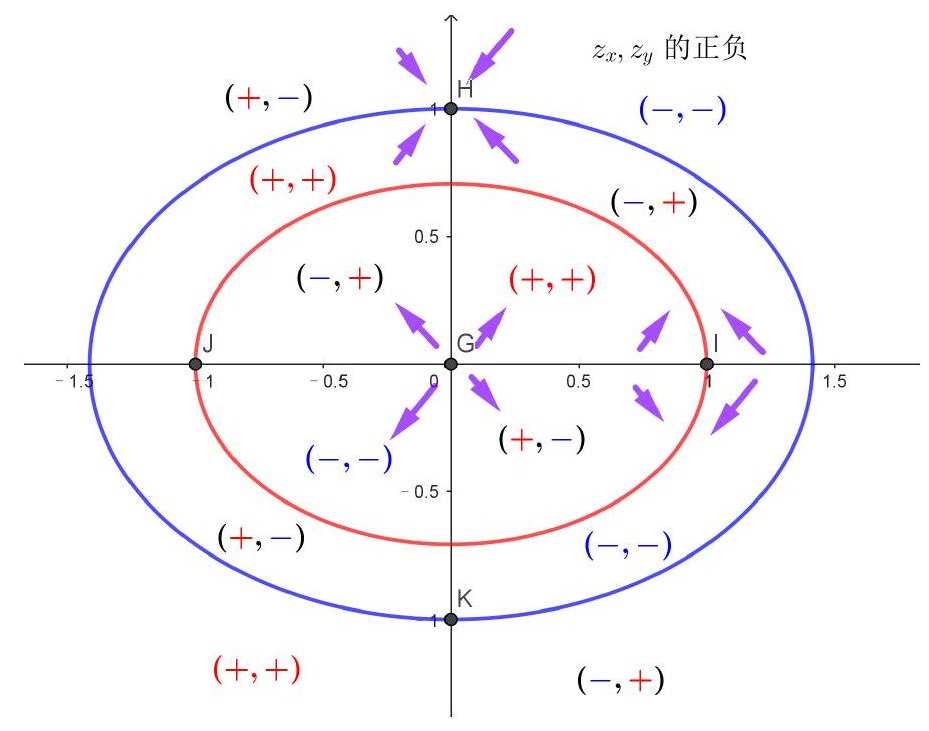
3.3 习题课讲解
3.3.1 高阶偏导数
例 3.3.1 (例1)
已知函数具有2阶连续偏导数,且函数满足。
-
(1)
-
求;
-
(2)
-
若,,求的表达式。
解
(1) 由链式法则得到
从而
因此
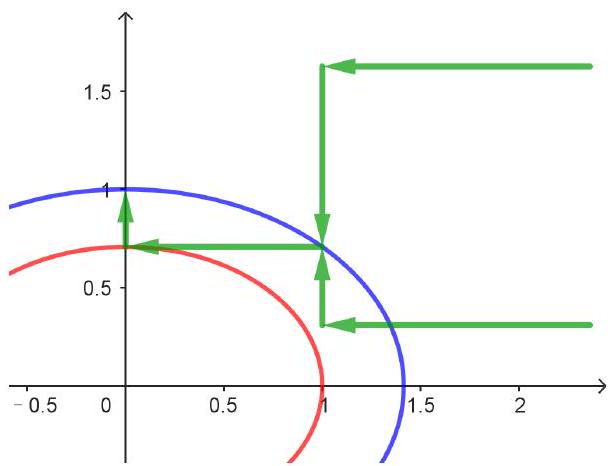
(2) 参考图3.3.1,我们有
进而
图 3.3.1: 例1(2)计算图示
另解(1)1
由变量替换以及Jacobi矩阵形式的链式法则,得到偏微分算子的关系
故有
因此
另解(1)2
由另解(1)1第一步解得
从而
例 3.3.2 (例2, )
设是阶正交矩阵,函数、。令,证明:
)
设是阶正交矩阵,函数、。令,证明:
证明
(1) 可直接通过全微分算子的协变变换证明:
或者利用梯度算子的逆变特性。坐标向量(逆变)的变换矩阵为,故基向量(协变)的变换矩阵,因此
(2) 可借助Hesse矩阵证明:
故
例 3.3.3 (例3, )
设满足
证明:
)
设满足
证明:
-
(1)
-
若满足,则满足。
-
(2)
-
。
证明
可微函数在单连通域上满足Cauchy-Riemann方程,从而解析。
(1) 在单连通域上调和,故存在解析函数使得,因此亦为解析函数,从而调和。
(2) 由(1)知调和。
例 3.3.4 ( )
设调和,令。证明:调和。
)
设调和,令。证明:调和。
证明
令、,其满足CR方程,由上例可知调和。由于是正交变换,故调和。
注
有关以上两题的更多信息,大家可以参考 王兆臻学长的习题课笔记。
3.3.2 Taylor展开
例 3.3.5 (例4, )
求在的带Peano余项的4阶Taylor公式和带Lagrange余项的1阶Taylor公式。
)
求在的带Peano余项的4阶Taylor公式和带Lagrange余项的1阶Taylor公式。
解
在的邻域中是函数。
由Peano余项Taylor公式的唯一性,这就是在处的Peano余项4阶Taylor公式。
计算的Hesse矩阵
所以
其中。
注
以下是带阶Lagrange余项的阶Taylor公式:
其中。具体来说,设,对于带2阶Lagrange余项的1阶Taylor公式,我们有
其中,,。所以本题需要计算到函数的所有二阶偏导数,以得到带Lagrange余项的1阶Taylor公式。
例 3.3.6 (例5)
求在的带Peano余项和带Lagrange余项的Taylor公式。
解
由广义二项式定理可得
故有
注意到
故有
因此
例 3.3.7 (例6, )
求在处的带Peano余项的2阶Taylor展开。
)
求在处的带Peano余项的2阶Taylor展开。
解
令、,则当时,有
注
以下是带Peano余项的阶Taylor公式:
具体来说,设,对于带2阶Lagrange余项的1阶Taylor公式,我们有
所以本题需要计算到函数的所有二阶偏导数,以得到带Peano余项的2阶Taylor公式。
特别提醒
Taylor公式中的易错点:
-
(1)
-
上文中提到的Taylor公式的阶。
-
(2)
-
Taylor多项式不能化简,需要保持因子。
-
(3)
-
在展开到第阶时需要除以。
-
(4)
-
Taylor公式的唯一性是指Taylor多项式的唯一性,余项的形式不一定唯一。如,利用上式可得其在原点附近的1阶Taylor公式为
如果借助一元Taylor公式,则有
3.3.3 极值与函数凹凸性
例 3.3.8 (例7)
求的极值、最值、值域。
解1
只求一阶导数,用梯度向量场分析函数单调性。由知的最小值为。求偏导可知
函数可微,极值点必然是驻点,从而,解得
由梯度向量场分布(图3.3.2)知,是最小值点,和是最大值点,和是鞍点,不是极值点。
现在讨论的值域。由对称性,只需讨论部分。显然是最小值。
当时,,,故关于严格减,即。由
知关于在区间上单增,在区间上单减,从而。由
知关于是减函数,从而。再由
知在取得最大值。所以对于任意以及任意,都有。
当时,则的符号与相同,故关于在上单增、在上单减,从而。
由连续函数的介值性质,的值域为区间。
图 3.3.2: 例7图示
解2
求驻点,计算Hesse矩阵,判断正、负定,分析极值类型。由知的最小值为。利用
知,存在使得当时。于是在有界闭集中的最大值点就是函数在整个定义域上的最大值点,因此是驻点,即函数值最大的驻点就是最大值点。
解3
利用极坐标
例 3.3.9 (例10, )
讨论函数的极值。
)
讨论函数的极值。
解
计算可知
解得驻点
随后分情况讨论。继续计算可得
代入第一类驻点可得
负定,所以是极大值点,极大值为。代入第二类驻点可得
特征值一正一负,所以是鞍点。
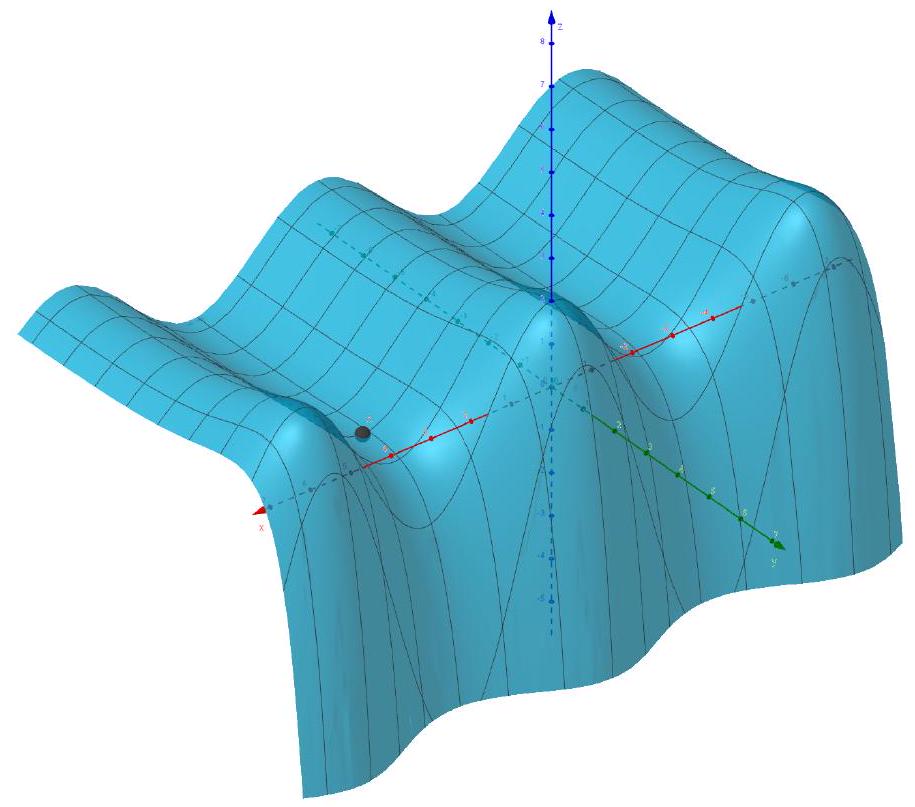
图 3.3.3: 的三维图像的透视图
例 3.3.10 (例11)
证明对任意、,都有
证明
记
计算可得
进一步计算可得
其中
所以关于是增函数。注意到,故关于在时取最小值,因此。
同理,故总是半正定,从而是凸函数,在上存在最小值。再注意到,所以是最小值。因此对任意,总有。
例 3.3.11 (例8)
设正数满足,求的取值范围。
解1
记
计算可得
所以
总是半正定,且定义域是凸集,所以是凸函数。
由得到,所以是最小值。又,所以的值域为。
解2
类似解1构造,计算可得
所以对给定的,关于在处取得最小值。继续构造
计算可得
所以关于在处取得最小值。如此类推,直到
由
知关于在处取得最小值。
在处取得最小值。因此在时取得最小值。又,所以的值域为。
3.3.4 与极值有关的证明题(1)
例 3.3.12 (例9)
设在上连续,在内,且
证明:当时,。
证明
反证法。假设存在满足、,因为在上连续,所以有最大值,于是 。因为沿边界,,所以,因此是极大值,从而半正定,故有
这与
矛盾。所以在内,恒有。
注
同理可得当时,,所以对所有成立。
例 3.3.13 (例9拓展1, )
设为有界开集,函数满足,且
证明:
)
设为有界开集,函数满足,且
证明:
-
(1)
-
若对所有成立,则对所有成立。
-
(2)
-
若对所有成立,则对所有成立。
证明
(1) 设为在上的最小值点。假设,则;又,由Fermat引理可知为驻点,且,矛盾!故,即对所有成立。
(2) 记、。构造函数
计算可得
由(1)可得对所有成立,因此
故对所有成立。
例 3.3.14 (例9拓展2, )
设区域,、、,证明:以下边值问题的解唯一。
)
设区域,、、,证明:以下边值问题的解唯一。
证明
设均满足该方程和边界条件,令,则满足
当时,令,则满足
在有界闭集上存在最小值点,显然。若,则有,故为极小值点,从而,矛盾!故对任意成立。同理可得,故,即。
当时,注意到
由可得,即。
综上所述,原边值问题具有唯一解。