5.1 第4次作业评讲
5.1.1 概念和计算部分
例 5.1.1
填空题:
-
(1)
-
( 73%)已知方程在点附近定义了可微隐函数,并且是该隐函数的驻点。则 ____。
73%)已知方程在点附近定义了可微隐函数,并且是该隐函数的驻点。则 ____。
-
(2)
-
( 32%)已知曲面上一点满足且直线
位于曲面在该点处的切平面上,则 ____。
32%)已知曲面上一点满足且直线
位于曲面在该点处的切平面上,则 ____。
-
(3)
-
( 79%) 在附近确定了隐函数,则在 处的Hesse矩阵的行列式为____。
79%) 在附近确定了隐函数,则在 处的Hesse矩阵的行列式为____。
-
(4)
-
( 82%)在点处, ____,其中、,是独立变量。
82%)在点处, ____,其中、,是独立变量。
-
(5)
-
( 78%)曲面 在点 处的切平面与坐标平面围成的四面体的体积为____。
78%)曲面 在点 处的切平面与坐标平面围成的四面体的体积为____。
解
(1) 两边对求导得到
令得到
代回原方程得到,从而,即。此处,满足隐函数定理条件。
(2) 直线方程可转写为,其过点、方向向量为;两点可确定切平面上的另一个方向向量;平面法向量满足、且。由此可得
解得或,故或。
另一种思路参见例4.3.10。直线的方向向量提供了曲面切平面的法向量,由此可以得到曲面的切平面方程;曲面方程求导也可以得到曲面切平面的方程;切点在曲面上,满足曲面方程。以上三个条件得到关于的三个方程组成的方程组,解这个方程组得到问题答案。
(3) 将代入得到
解得
从而
这是在处的二阶Taylor公式,由此得到在原点处的Hesse矩阵为
也可以对方程求导,得到在原点处的所有二阶偏导数,但计算过程比上述(间接)Taylor展开要复杂。
(4) 由满足的方程,验证,从而由隐函数定理得到隐函数,恒等式对求导得到
解得,代入可得
(5) 切平面方程为,亦即,其在轴上的截距分别为,围成的四面体体积为。
5.1.2 解答和证明部分
例 5.1.2 (解答题1,
 ,
, 70%)
记为阶实数方阵组成的线性空间,是单位矩阵。考虑矩阵方程
70%)
记为阶实数方阵组成的线性空间,是单位矩阵。考虑矩阵方程
-
(1)
-
证明上述方程有唯一解满足,且关于是的。
-
(2)
-
求在处带Peano余项的二阶Taylor公式。
解
(1) 构造函数,则。注意到 线性
意味着、可逆。根据隐函数定理,使得
线性
意味着、可逆。根据隐函数定理,使得 因为是函数,也是函数。
因为是函数,也是函数。
全局唯一性的证明比较复杂。 设是任意两个满足的解,令,我们证明非空且既开又闭,则。
设是任意两个满足的解,令,我们证明非空且既开又闭,则。
由题知,故非空。
对任意,由隐函数定理可知使得,故为开集。
给定满足,由可知
由此可知,故为闭集。
(2) 原方程写成分量形式可得
对求导可得
写回矩阵形式可得
令,则,代入解得。 同理,再对求导可得
代入解得。故在处的二阶Taylor公式为
同理,再对求导可得
代入解得。故在处的二阶Taylor公式为
解
参见例4.3.15。
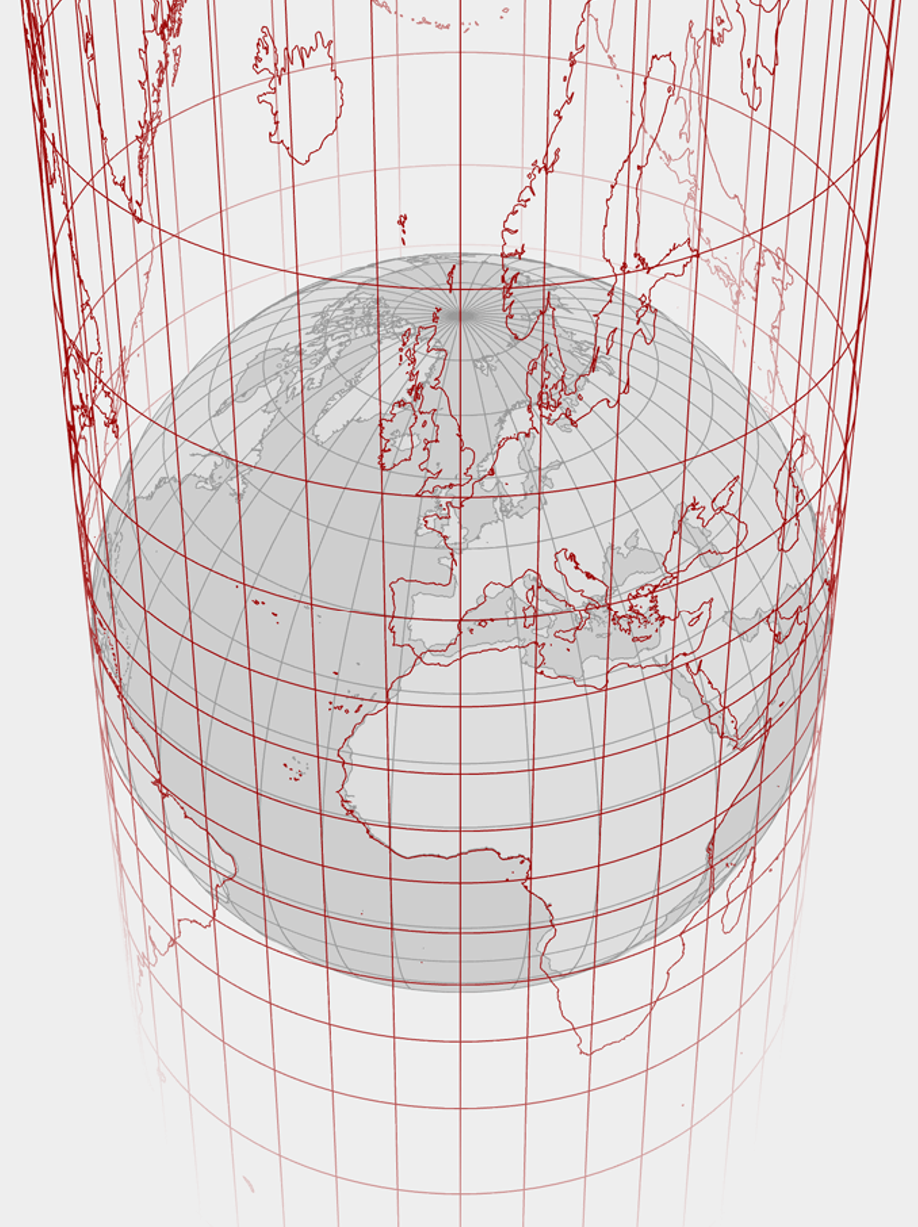
图 5.1.1: Mercator地图
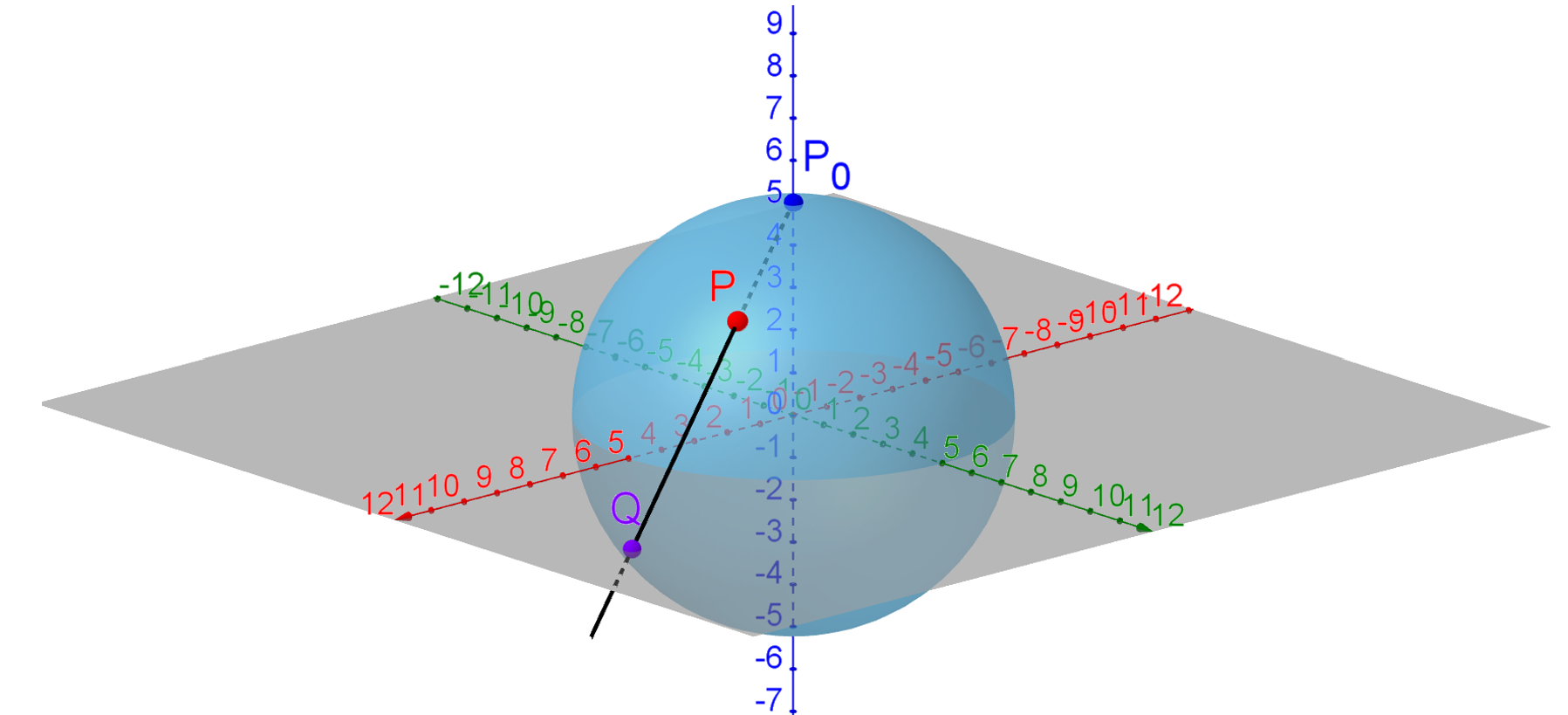
图 5.1.2: 球极投影
证明
不妨设球为底部放置于原点的单位球,类似Mercator地图的做法,首先找到球极投影之间的函数映射关系。由几何关系可知
设是球面上过点的一条光滑曲线,则把映为平面上过点的一条光滑曲线
设、,计算可知的速度向量为
球面上处的两个切向量的内积为
夹角的余弦为
上相应的速度向量为
柱面上处的两个切向量的内积为
夹角的余弦为
故,即球极投影是保角变换。
证明
函数的非退化临界点需满足 由于连续、连续,故使得
由于连续、连续,故使得
欲证函数在附近有唯一的临界点,等价于证明方程在附近有关于的唯一解 。注意到可逆
。注意到可逆 ,由隐函数定理可知使得
,由隐函数定理可知使得 且此时。
且此时。
 73%)已知方程
73%)已知方程 32%)已知曲面
32%)已知曲面 79%)
79%)  82%)在点
82%)在点 78%)曲面
78%)曲面 


 设
设 同理,再对
同理,再对

 ,
, 94%)
沿地球(假想为标准的球)沿赤道包裹一个圆柱面(圆柱面与球面沿赤道相切),从地球中心沿射线方向把地球表面上的点投射到圆柱面上,再沿一条圆柱面上与赤道垂直的一条直线将圆柱面剪开,把圆柱面摊开为一个平面,这样得到一张地图,这样的地图以经线和纬线为坐标。问:对维度做怎样的变换,可以使地图上经线和纬线方向不变,但地球上两条相交曲线的夹角和这两条曲线在地图上相应点处的夹角保持一致?
94%)
沿地球(假想为标准的球)沿赤道包裹一个圆柱面(圆柱面与球面沿赤道相切),从地球中心沿射线方向把地球表面上的点投射到圆柱面上,再沿一条圆柱面上与赤道垂直的一条直线将圆柱面剪开,把圆柱面摊开为一个平面,这样得到一张地图,这样的地图以经线和纬线为坐标。问:对维度做怎样的变换,可以使地图上经线和纬线方向不变,但地球上两条相交曲线的夹角和这两条曲线在地图上相应点处的夹角保持一致?


