4.2 知识点复习

4.2.1 再谈隐函数定理

隐函数定理：

• 条件：特解、特解处线性近似方程非退化（对因变量的Jacobi矩阵可逆）。
• 结论：隐函数的局部存在性、唯一性、可微性，导数计算公式（链式法则）。

这里我们不推荐大家记忆隐函数定理中求隐函数导数（偏导数）的公式，而推荐大家熟练运用链式法则（或全微分）：$$\begin{array}{}\text{(1)}& \begin{array}{rl}0& ={\partial }_{\mathit{x}}[F(\mathit{x},g(\mathit{x}))]={\partial }_{\mathit{x}}F(\mathit{x},g(\mathit{x}))+{\partial }_{y}F(\mathit{x},g(\mathit{x})){\partial }_{\mathit{x}}g(\mathit{x})\\ \Rightarrow {\partial }_{\mathit{x}}g(\mathit{x})& =-[{\partial }_{\mathit{y}}F(\mathit{x},g(\mathit{x})){]}^{-1}{\partial }_{\mathit{x}}F(\mathit{x},g(\mathit{x}))\end{array}\end{array}$$

4.2.2 再谈曲线和曲面 (1)：空间曲面的表达式

空间曲面都可以通过下面两种形式表示¹。此处我们以最常见的${\mathbb{R}}^3$中的${\mathbb{R}}^2$曲面为例。

方程表示（又称水平集）

$F(x,y,z)=0$，其中$F_x,F_y,F_z$中至少有一个非零。

对于曲面上的光滑曲线$\mathit{x}(t):=(x(t),y(t),z(t){)}^{\mathrm{T}}$，设${\mathit{x}}_0=\mathit{x}(t_0)$，求导可得$$\begin{array}{}\text{(2)}& 0=F(x(t),y(t),z(t))\Rightarrow 0={\frac{\mathrm{d}}{\mathrm{d}t}F(x(t),y(t),z(t))|}_{t=t_0}=\mathrm{\nabla }F({\mathit{x}}_0)\cdot {\mathit{x}}^{\prime }(t_0)\end{array}$$ 即曲面在${\mathit{x}}_0$处的切向量总与$F$在${\mathit{x}}_0$处的梯度向量正交。

对曲面上的点${\mathit{x}}_0$，$\mathrm{\nabla }F({\mathit{x}}_0)$是曲面的法向量，故切平面方程为$$\begin{array}{}\text{(3)}& \mathrm{\nabla }F({\mathit{x}}_0)\cdot (\mathit{x}-{\mathit{x}}_0)=\mathrm{d}F({\mathit{x}}_0)(\mathit{x}-{\mathit{x}}_0)=0\end{array}$$ 法线方程可以写成参数形式$$\begin{array}{}\text{(4)}& \mathit{x}={\mathit{x}}_0+t\mathrm{\nabla }F({\mathit{x}}_0),t\in \mathbb{R}\end{array}$$ 或比例形式（直线的点—向式方程）²$$\begin{array}{}\text{(5)}& \frac{x-x_0}{F_x(x_0,y_0,z_0)}=\frac{y-y_0}{F_y(x_0,y_0,z_0)}=\frac{z-z_0}{F_z(x_0,y_0,z_0)}\end{array}$$

参数方程表示（又称参数曲面）

$\mathit{x}(u,v):=(x(u,v),y(u,v),z(u,v){)}^{\mathrm{T}}$，其中$(u,v)\in D\subseteq {\mathbb{R}}^2$，且$\frac{\partial (x,y)}{\partial (u,v)},\frac{\partial (y,z)}{\partial (u,v)},\frac{\partial (z,x)}{\partial (u,v)}$中至少有一个可逆。

对于曲面上的光滑曲线$\mathit{x}(t):=\mathit{x}(u(t),v(t))$，设${\mathit{x}}_0=\mathit{x}(t_0)$，求导可得$$\begin{array}{}\text{(6)}& {\mathit{x}}^{\prime }(t_0)={\frac{\mathrm{d}}{\mathrm{d}t}\mathit{x}(u(t),v(t))|}_{t=t_0}={\frac{\partial \mathit{x}}{\partial u}|}_{\mathit{x}={\mathit{x}}_0}{u}^{\prime }(t_0)+{\frac{\partial \mathit{x}}{\partial v}|}_{\mathit{x}={\mathit{x}}_0}{v}^{\prime }(t_0)\end{array}$$ 因此曲面在${\mathit{x}}_0$处的切空间是由向量$\frac{\partial \mathit{x}}{\partial u}$和$\frac{\partial \mathit{x}}{\partial v}$（在${\mathit{x}}_0$处的值）张成的线性空间，切平面方程为$$\begin{array}{}\text{(7)}& \mathit{x}={\mathit{x}}_0+\xi {\frac{\partial \mathit{x}}{\partial u}|}_{\mathit{x}={\mathit{x}}_0}+\eta {\frac{\partial \mathit{x}}{\partial v}|}_{\mathit{x}={\mathit{x}}_0},\xi ,\eta \in \mathbb{R}\end{array}$$ 或写成$$\begin{array}{}\text{(8)}& \left|\begin{array}{ccc}x-x_0& x_u(u_0,v_0)& x_v(u_0,v_0)\\ y-y_0& y_u(u_0,v_0)& y_v(u_0,v_0)\\ z-z_0& z_u(u_0,v_0)& z_v(u_0,v_0)\end{array}\right|=0\end{array}$$ $$\begin{array}{}\text{(9)}& det\frac{\partial (y,z)}{\partial (u,v)}(x-x_0)+det\frac{\partial (z,x)}{\partial (u,v)}(y-y_0)+det\frac{\partial (x,y)}{\partial (u,v)}(z-z_0)=0\end{array}$$

因此，在直角坐标系下，曲面的法向量为$$\begin{array}{}\text{(10)}& {(det\frac{\partial (y,z)}{\partial (u,v)},det\frac{\partial (z,x)}{\partial (u,v)},det\frac{\partial (x,y)}{\partial (u,v)})}^{\mathrm{T}}\end{array}$$ 法线方程也可以仿照前面的讨论写出，有参数形式和比例形式。

借助向量积，曲面的法向量可以表示为$\frac{\partial \mathit{x}}{\partial u}\times \frac{\partial \mathit{x}}{\partial v}$。

4.2.3 再谈曲线和曲面 (2)：空间曲线的切线与法平面

我们仍以最常见的${\mathbb{R}}^3$中的曲线为例。给定曲线的参数化表示$\mathit{x}(t):=(x(t),y(t),z(t){)}^{\mathrm{T}}$，设${\mathit{x}}_0=\mathit{x}(t_0)$，则曲线在点${\mathit{x}}_0$处的切向量为${\mathit{x}}^{\prime }(t_0)$，切线方程为$$\begin{array}{}\text{(11)}& \mathit{x}={\mathit{x}}_0+\xi {\mathit{x}}^{\prime }(t_0),\xi \in \mathbb{R}\end{array}$$ 因此法平面为$$\begin{array}{}\text{(12)}& {\mathit{x}}^{\prime }(t_0)\cdot (\mathit{x}-{\mathit{x}}_0)=x^{\prime }(t_0)(x-x_0)+y^{\prime }(t_0)(y-y_0)+z^{\prime }(t_0)(z-z_0)=0\end{array}$$

曲线的另一种表达方式为两个曲面的交，即$$\begin{array}{}\text{(13)}& \{\begin{array}{l}F(x,y,z)=0\\ G(x,y,z)=0\end{array}\end{array}$$ 其中$\frac{\partial (F,G)}{\partial (x,y,z)}$行满秩。曲线的切线方程由两个曲面的切平面方程联立而得，即为$$\begin{array}{}\text{(14)}& \{\begin{array}{l}\mathrm{\nabla }F\cdot (\mathit{x}-{\mathit{x}}_0)=0\\ \mathrm{\nabla }G\cdot (\mathit{x}-{\mathit{x}}_0)=0\end{array}\end{array}$$ 由此可见法空间是二维空间，由$\mathrm{\nabla }F$和$\mathrm{\nabla }G$张成，所以法平面方程为$$\begin{array}{}\text{(15)}& \left|\begin{array}{ccc}x-x_0& F_x(x_0,y_0,z_0)& G_x(x_0,y_0,z_0)\\ y-y_0& F_y(x_0,y_0,z_0)& G_y(x_0,y_0,z_0)\\ z-z_0& F_z(x_0,y_0,z_0)& G_z(x_0,y_0,z_0)\end{array}\right|=0\end{array}$$

借助向量积，曲线的切向量可以表示为$\mathrm{\nabla }F\times \mathrm{\nabla }G$。

4.2.4 再谈曲线和曲面 (3)：总结

以下是三维空间中的曲线和曲面总结：

无论采用哪种形式，切平面（切线）方程都可以通过一阶Taylor展开得到。

4.2.5 *向量的向量积

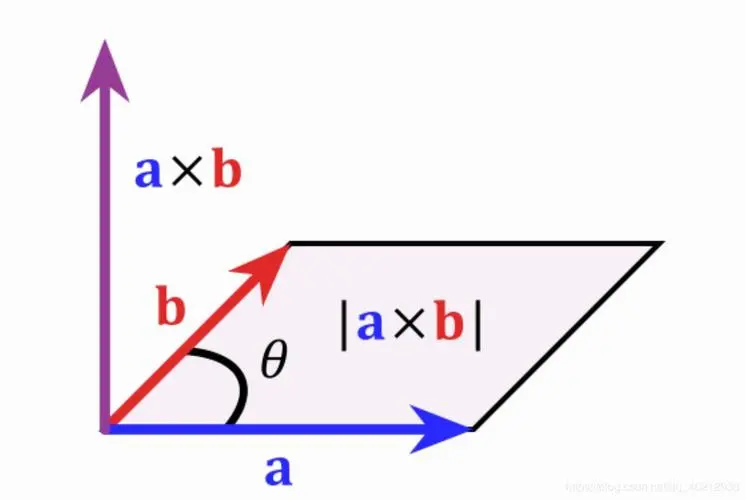
向量的向量积（叉乘）仅在3维空间³中有定义，为$$\begin{array}{}\text{(16)}& \mathit{a}\times \mathit{b}=\left|\begin{array}{ccc}\mathit{i}& \mathit{j}& \mathit{k}\\ a_1& a_2& a_3\\ b_1& b_2& b_3\end{array}\right|=\left(\begin{array}{c}{a}_2{b}_3-a_3{b}_2\\ a_3{b}_1-a_1{b}_3\\ a_1{b}_2-a_2{b}_1\end{array}\right)\end{array}$$

向量积的几何意义是：$\mathit{a}\times \mathit{b}$是与$\mathit{a}$和$\mathit{b}$都垂直的向量，且$\mathit{a},\mathit{b},\mathit{a}\times \mathit{b}$构成右手坐标系，其大小为$$\begin{array}{}\text{(17)}& |\mathit{a}\times \mathit{b}|=|\mathit{a}||\mathit{b}|\sin \theta \end{array}$$ 恰为由$\mathit{a}$和$\mathit{b}$张成的平行四边形的面积，其中$\theta$为$\mathit{a},\mathit{b}$之间的夹角。容易证明：对于${\mathbb{R}}^3$中向量$\mathit{a},\mathit{b},\mathit{c}$张成的平行六面体，其体积为$$\begin{array}{}\text{(18)}& V=|\mathit{a}\cdot (\mathit{b}\times \mathit{c})|=|det(\mathit{a},\mathit{b},\mathit{c})]|\end{array}$$ 因此向量积的主要应用是计算平行四边形或三角形的面积，以及计算平面的法向量。

(a) 向量积的几何意义

(b) 右手坐标系

向量积满足以下性质：

(1)

反交换律：$\mathit{a}\times \mathit{b}=-\mathit{b}\times \mathit{a}$；

(2)

分配律：$\mathit{a}\times (\mathit{b}+\mathit{c})=\mathit{a}\times \mathit{b}+\mathit{a}\times \mathit{c}$；

(3)

与数乘的结合律：$(\lambda \mathit{a})\times \mathit{b}=\mathit{a}\times (\lambda \mathit{b})=\lambda (\mathit{a}\times \mathit{b})$；

(4)

与向量加法的结合律：$\mathit{a}\times (\mathit{b}+\mathit{c})=\mathit{a}\times \mathit{b}+\mathit{a}\times \mathit{c}$；

(5)

与向量的点积的关系：$\mathit{a}\times (\mathit{b}\times \mathit{c})=(\mathit{a}\cdot \mathit{c})\mathit{b}-(\mathit{a}\cdot \mathit{b})\mathit{c}$。

(6)

与向量的混合积的关系：$\mathit{a}\cdot (\mathit{b}\times \mathit{c})=\mathit{b}\cdot (\mathit{c}\times \mathit{a})=\mathit{c}\cdot (\mathit{a}\times \mathit{b})$。

4.2.6 *一阶线性偏微分方程的通解法和特征线法

设$\mathit{x}=(x_1,\cdots ,x_n)\in V\subseteq {\mathbb{R}}^n$，函数$u:\mathit{x}\mapsto u(x_1,\cdots ,x_n)$，则一个微分方程指的是联系未知函数$u$和它的（偏）导数的方程，一般具有如下形式：$$\begin{array}{}\text{(19)}& F(\mathit{x},u,\frac{\partial u}{\partial x_1},\cdots ,\frac{\partial u}{\partial x_n},\cdots ,\frac{{\partial }^{m_1+\cdots +m_n}u}{\partial x_1^{m_1}\cdots \partial x_n^{m_n}})=0\end{array}$$ 其中$V$称为方程的求解域。常微分方程(ODE)是指未知函数为单变量函数的方程；偏微分方程(PDE)是指未知函数为多变量函数的方程；线性方程是指$F$为线性函数的方程，具有形式$\mathcal{L}u=f$，其中$\mathcal{L}$为线性微分算子；若$\mathcal{L}u=0$则称为齐次方程。方程组出现的未知函数（偏）导数的最高阶数称为方程的阶。

设在空间$V\subseteq {\mathbb{R}}^n$内方程$$\begin{array}{}\text{(20)}& F(\mathit{x},u,\frac{\partial u}{\partial x_1},\cdots ,\frac{\partial u}{\partial x_n},\cdots ,\frac{{\partial }^{m_1+\cdots +m_n}u}{\partial x_1^{m_1}\cdots \partial x_n^{m_n}})=0\end{array}$$ 有解$u=u(\mathit{x})$且$u$具有方程中出现的各阶连续偏导数，则称其为方程的古典解。$m$阶方程含有$m$个任意函数的解称为方程的通解，不含任意函数或任意常数的解称为方程的一个特解。

一般地，一阶线性偏微分方程具有下面的形式$$\begin{array}{}\text{(21)}& \sum _{i=1}^n{a}_i(x_1,\cdots ,x_n)\frac{\partial u}{\partial x_i}+p(x_1,\cdots ,x_n)u=q(x_1,\cdots ,x_n)\end{array}$$ 当一阶线性偏微分方程的一阶导数项只有一个时，即$$\begin{array}{}\text{(22)}& \frac{\partial u}{\partial x_1}+p(x_1,\cdots ,x_n)u=q(x_1,\cdots ,x_n)\end{array}$$ 此时可以直接使用积分因子法来求解此题，只不过需要把积分常数换成关于$x_2,\cdots ,x_n$的函数即可，亦即$$\begin{array}{}\text{(23)}& u(x_1,\cdots ,x_n)={\mathrm{e}}^{-\int p\mathrm{d}{x}_1}(\int {\mathrm{e}}^{\int p\mathrm{d}{x}_1}q\mathrm{d}{x}_1+f(x_2,\cdots ,x_n))\end{array}$$ 其中$f\in \mathcal{C}({\mathbb{R}}^{n-1})$。

当一阶线性偏微分方程的一阶导数项不止一个时，我们可以尝试利用换元法来消除多余的一阶导数项。一种常见的方法是特征线法。设$\mathit{x}\in {\mathbb{R}}^n$，$b_1,\cdots ,b_n,c,f,u$均为关于$\mathit{x}$的函数，给定区域$D$上关于$u$的一阶线性偏微分方程$$\begin{array}{}\text{(24)}& \sum _{i=1}^n{b}_i\frac{\partial u}{\partial x_i}+cu=f\end{array}$$ 则特征线法的步骤如下：

1.

列特征方程组$$\begin{array}{}\text{(25)}& \frac{\mathrm{d}{x}_1}{b_1}=\cdots =\frac{\mathrm{d}{x}_n}{b_n}\end{array}$$

2.

求出它的$n-1$个线性无关的隐式通解$$\begin{array}{}\text{(26)}& {\phi }_i(x_1,\cdots ,x_n)=h_i,i=1,\cdots ,n-1\end{array}$$ 称为$n-1$个首次积分或特征线。

3.

选择与${\phi }_1,\cdots ,{\phi }_{n-1}$线性无关的函数${\phi }_n$，亦即使得如下Jacobi矩阵可逆$$\begin{array}{}\text{(27)}& J=\frac{\partial ({\phi }_1,\cdots ,{\phi }_n)}{\partial (x_1,\cdots ,x_n)}\end{array}$$

4.

作如下自变量变换$$\begin{array}{}\text{(28)}& {\xi }_i={\phi }_i(x_1,\cdots ,x_n),i=1,\cdots ,n\end{array}$$ 则原偏微分方程可化为仅含有一项一阶偏导数的形式，即$$\begin{array}{}\text{(29)}& \left(\sum _{i=1}^n{b}_i\frac{\partial {\phi }_n}{\partial x_i}\right)\frac{\partial \tilde{u}}{\partial {\xi }_n}+c\tilde{u}=f\end{array}$$ 特别地，当$c=f=0$时，令${\xi }_n=x_n$，方程可化为$$\begin{array}{}\text{(30)}& \frac{\partial \tilde{u}}{\partial {\xi }_n}=0\end{array}$$ 此时方程的解为$$\begin{array}{}\text{(31)}& u(x_1,\cdots ,x_n)=\tilde{u}({\xi }_1(\mathit{x}),\cdots ,{\xi }_n(\mathit{x}))=F({\phi }_1(\mathit{x}),\cdots ,{\phi }_{n-1}(\mathit{x}))\end{array}$$ 其中$F\in {\mathcal{C}}^1({\mathbb{R}}^{n-1})$是任意函数。