9.1 第7次作业评讲
例 9.1.1 (题1, 86%)
设曲线,计算:
86%)
设曲线,计算:
解
弧长微元为
代入积分中可得
例 9.1.2 (题2, 95%)
马鞍面被圆柱面所截,计算截得的有界部分曲面的面积。
95%)
马鞍面被圆柱面所截,计算截得的有界部分曲面的面积。
解
曲面的一个合适的参数化方案就是选用极坐标系,亦即
计算可得
进一步计算可得
故面积微元为
因此
例 9.1.3 (题3, 82%)
曲线的线密度为,计算曲线的质量。
82%)
曲线的线密度为,计算曲线的质量。
解
由于对称性,我们只需要计算曲线在第一象限中的质量,随后乘以即可。在第一象限中可化为,则弧长微元为
因此
例 9.1.4 (题4, 100%)
设中曲面,计算:
100%)
设中曲面,计算:
解
计算可得
进一步计算可得
故面积微元为
因此
例 9.1.5 (题5, 91%)
设,为中依次连接的闭合折线,计算:。
91%)
设,为中依次连接的闭合折线,计算:。
解
设,则
弧长微元为
计算可得
因此
例 9.1.6 (题6, 73%)
如图,是单位球面上的一条曲线,以为起点、为终点(图9.1.1),计算:
73%)
如图,是单位球面上的一条曲线,以为起点、为终点(图9.1.1),计算:
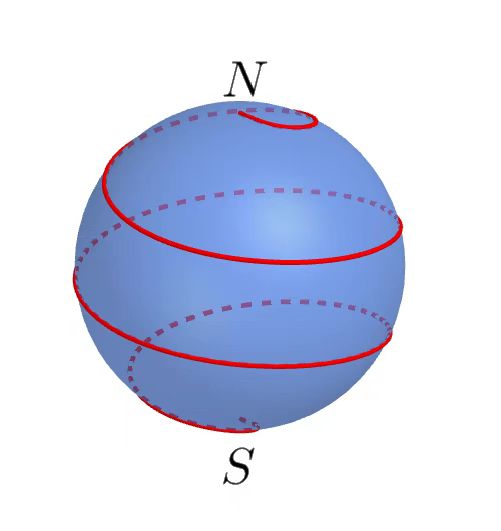
图 9.1.1: 一条从到的曲线
解
注意到
故原积分可化为
例 9.1.7 (题7, 86%)
空间曲线为柱面与平面的交线,它围绕轴的正方向逆时针旋转,计算
86%)
空间曲线为柱面与平面的交线,它围绕轴的正方向逆时针旋转,计算
解
注意到
设为围成的平面区域的面积,利用Green公式可得
例 9.1.8 (题8, 100%)
(2022春期末考试)已知曲线积分与积分路径无关(只与曲线的起点和终点有关),则实数 ____。
100%)
(2022春期末考试)已知曲线积分与积分路径无关(只与曲线的起点和终点有关),则实数 ____。
解
本题等价于:对任意有向(简单)闭曲线,都满足
设为的边界,由Green公式可得
为了使上式对任意区域成立,必须有。
例 9.1.9 (题9, 95%)
设有向曲线,参数增加方向与曲线正向一致,计算:
95%)
设有向曲线,参数增加方向与曲线正向一致,计算:
解
直接代入计算可得
例 9.1.10 (题10, 100%)
设,记为单位圆周,逆时针为正向,计算:
100%)
设,记为单位圆周,逆时针为正向,计算:
解
凑全微分可得
故有
 73%)
如图,
73%)
如图,
 73%)
如图,
73%)
如图,