7.2 知识点复习
7.2.1 一元定积分回顾
重要概念回顾
-
(1)
-
Riemann和:设为的一个划分,选定区间的代表元,则在上的Riemann和为
-
(2)
-
Riemann可积:设,若,使得,,使得对任意划分,
则称在上Riemann可积,为在上的Riemann积分(定积分),记作
-
(3)
-
Darboux上下和:设有界,给定划分,定义
则显然有
-
(4)
-
Darboux可积:设,若,使得,存在划分,使得
则称在上Darboux可积。
-
(5)
-
零测集:设,若,可数个区间,使得
则称为零测集。
重要定理回顾
-
(1)
-
以下三个命题等价:
- (Riemann)在上Riemann可积;
- (Darboux)在上Darboux可积;
- (Lebesgue)在上有界,且的间断点集是零测集。
-
(2)
-
上的所有连续函数可积,上的所有单调函数可积。
7.2.2 重积分的概念
重要概念回顾
-
(1)
-
矩形:称
为中的一个矩形,则为的维体积。
-
(2)
-
划分:称为的一个划分,若
- ,其中均为矩形;
- ,即两两矩形之间的交集是它们的公共边界。
-
(3)
-
Riemann和:设,选定的代表元,则在上的Riemann和为
称在上Riemann可积,若,使得,,使得对任意划分,
在上的Riemann积分记作
当时,该Riemann积分又称为()重积分。
-
(4)
-
Darboux和:设,定义
在上Darboux可积若……。
-
(5)
-
Jordan可测:称为Jordan可测集,若为零测集,即,可数个矩形,使得
-
(6)
-
Jordan可测集上的积分:设为有界闭的Jordan可测集,。令矩形满足,定义函数
若在上可积,则称在上可积,且
重要定理回顾
-
(1)
-
以下三个命题等价:
- (Riemann)在上Riemann可积;
- (Darboux)在上Darboux可积;
- (Lebesgue)在上有界,且的间断点集是零测集。
-
(2)
-
上的所有连续函数可积。
-
(3)
-
若为有界闭集且为零测集,则上的所有连续函数可积。
-
(4)
-
示性函数
在上可积,且
-
(5)
-
重积分的性质:令表示上所有Riemann可积函数的集合,则
- 线性:是一个线性空间,即,,都有,且成立
- 保号性:设,若,则
- 区域可加性:设,,且,则
- 三角不等式:,且成立,故
- Cauchy-Schwarz不等式:设,则,且成立
- 积分中值定理:设为连通集,且,,则,使得
若下式中分母不为零,则有
称为在上关于的(加权)平均值。
7.2.3 重积分的计算
计算重积分的基本方法:
- 将集合和函数分解为简单的部分;
- 换元以化简或;
- 降低重数(维数)到一元积分或累次积分;
- 数值积分法、Monte Carlo方法等。
重要定理回顾
(Fubini)若为有界闭的Jordan可测集,,,则,存在,其中,且
应用
-
(1)
-
证明:
-
(2)
-
设为三个圆柱、、所围成的有界闭区域,证明:
-
(3)
-
积分换序练习。设,证明:
设,证明:
证明:
-
(4)
-
设是由、、围成的两个有界闭区域,证明:
注
积分是从右向左计算的!例如
7.2.4 重积分的换元
重要定理回顾
设为有界闭的Jordan可测集,;为有界闭的Jordan可测集,是的微分同胚(的可逆坐标变换),则在点附近有
因此
应用
-
(1)
-
常用坐标系的体积元:
- 极坐标系:;
- 柱坐标系:;
- 球坐标系:。
-
(2)
-
设为有界闭的Jordan可测集,满足;函数满足。记、,证明:
-
(3)
-
设,利用换元证明:
-
(4)
-
设,利用极坐标换元证明:
-
(5)
-
设,利用换元证明:
-
(6)
-
设,为阶实对称正定矩阵,利用谱分解换元证明:
-
(7)
-
质心:设,其密度分布函数为,则其质心满足
-
(8)
-
设,其质量均匀分布,则的质心满足:
-
(9)
-
期望:设为概率空间,为随机变量,则其概率密度函数的定义为
其期望为
-
(10)
-
在(均匀分布)上取个独立随机变量,则其最小值的期望为。
-
(11)
-
证明万有引力定律对质量均匀分布的球体同样适用,即证明:
-
(12)
-
证明有心力场的(广义)Kepler第二定律。设质点在平面上的运动轨迹为,其中。设为行星与恒星连线在内扫过的面积,令,则有
因此的面积为
由的任意性可得
因此
故与共线,即为有心力场。
7.2.5 补充:利用不等式方法确定积分域和积分限
许多重积分的区域是由个曲面(包括平面)所围成的有界区域表示的,我们首先需要确定该区域对应的不等式表示。理论上,我们需要依次分析个不等式组的解集是否有界,但可以通过观察减少搜索范围。以为例,常见的剪枝方法为:
命题 7.2.1
若区域中与有关的所有显式不等式的符号全部相同,即(或),则必定无界。
推论 7.2.2
若与有关的等式仅有2个,亦即、,则必有或之一成立。这类自变量通常是我们突破的重点。
得到不等式给出的积分区域后,我们还需要将积分域表示为积分限的形式,实质就是解不等式。设积分顺序为。
-
(1)
-
用不等式表示有界区域。
-
(2)
-
对于自变量满足的个不等式,依次解出它们的显式形式,即
其中表示去掉的自变量向量。如果解出来的不等式不能表示为上面的“类区间形式”,意味着积分区域需要分块。
-
(3)
-
由此得到所有自变量满足的显式不等式,亦即
方便起见,将上式改写为
-
(4)
-
若,则的积分区域为,其中表示去掉在之前(含自身)积分的自变量向量,因为后积分的自变量区域不能与先积分的自变量有关。
-
(5)
-
若,记前个自变量的积分区域为
则的积分区域为在原有不等式的基础上,消去后得到的新不等式
-
(6)
-
最终的积分限可表示为
例 7.2.3 (例1改)
改变区域的积分次序:
解
对于,先对积分可得
对于,先对积分可得
因此
例 7.2.4 (例2改)
设有界区域由、、、、围成,按以下次序确定积分上下限:
-
(1)
-
先对积分,再对积分,最后对积分。
-
(2)
-
形式最简单的积分次序。
解
首先确定各不等式的符号(还是)。我们从入手,必有或之一成立。
对于,此时有(已确定3个符号)。
- 若,则,无界。
- 若,则根据边界,必有或之一成立,均无界。
故这种情况不成立。
对于,有,结合可得(已确定3个符号)。
- 若,则,无界。
- 若,则。根据边界,必有或之一成立,前者无界,后者有界。
由此我们定出了所有不等式的符号:、、、。
(2) 显然,形式最简单的积分次序为:
即先对积分,再对(或)积分,最后对(或)积分。
(1) 如先对积分,则有,此时满足
解得
因此
如需去掉,还需要分和两种情况讨论,前者需要成立,故需要分为3个区域:
例 7.2.5 (例3改)
设有界区域由、、、、围成,选择合适的坐标系和积分次序确定积分上下限。
解
类似例 7.2.4,我们从入手,得到。
- 若,则,无界。
- 若,则由的对称性可知无界。
- 若且,则有、,有界。
因此且。
若,则,故有、,因此
如使用柱坐标系,则有,。因此
若,则当时有,当时有,故需要分为2个区域:
如使用柱坐标系,则仍有,。因此
例 7.2.6 (例4改)
改变区域的积分次序:
解
最简单的改变方式是对换,此处从略。将改写为
先对积分:,此时满足
解得
因此
如需去掉,还需要分和两种情况讨论,故需要分为2个区域:
7.2.6 补充:三维空间中的重积分计算
二重积分:画线法

图 7.2.1: 二重积分的画线法
二重积分的积分区域可以很方便地画出来,此时可借助画线法来确定积分限。如图 7.2.1(左)所示,我们可以
- 垂直于轴画线(的等值线),先确定的值,意味着最后对积分;
- 上下平移该线即可得到的取值范围;
- 画的线与区域的交线就是的积分限,为关于的函数。
同理,我们也可以
- 垂直于轴画线(的等值线),先确定的值,意味着最后对积分;
- 左右平移该线即可得到的取值范围;
- 画的线与区域的交线就是的积分限,为关于的函数。
有时,画的线与区域的交线并不是连续的,则积分区域需要分块,如图 7.2.1(右)所示。此时的积分限为,的积分限为。

图 7.2.2: 二重积分的极坐标画线法
除了对的画线法以外,我们还可以利用极坐标来确定积分限。如图 7.2.2 所示,我们可以
- 以原点为端点、为倾角画射线(的等值线),先确定的值,意味着最后对积分;
- 逆、顺时针旋转射线即可得到的取值范围;
- 画的线与区域的交线就是的积分限,为关于的函数。
或者
- 以原点为圆心、为半径画圆(的等值线),先确定的值,意味着最后对积分;
- 放大、缩小该圆即可得到的取值范围;
- 画的线与区域的交线就是的积分限,为关于的函数。
三重积分:先一后二投影法
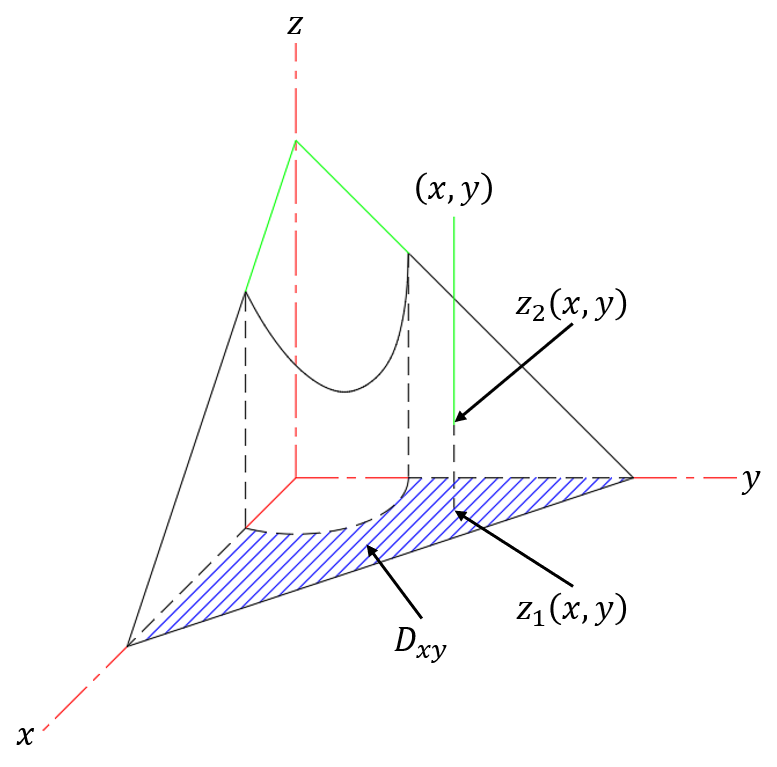
图 7.2.3: 三重积分的先一后二投影法
与二重积分类似,三重积分也可以借助划线法来确定积分限;如图 7.2.3 所示。
- 垂直于某一个坐标平面(不妨设为)画线(的等值线),确定了2个坐标值,意味着最后对积分,故称为“先一后二法”。
- 前后、左右平移该线即可得到的取值范围,这相当于将积分区域向平面投影,故称为“投影法”;
- 画的线与区域的交线就是的积分限,为关于的函数。
其他坐标平面也是类似的。
三重积分:先二后一截面法
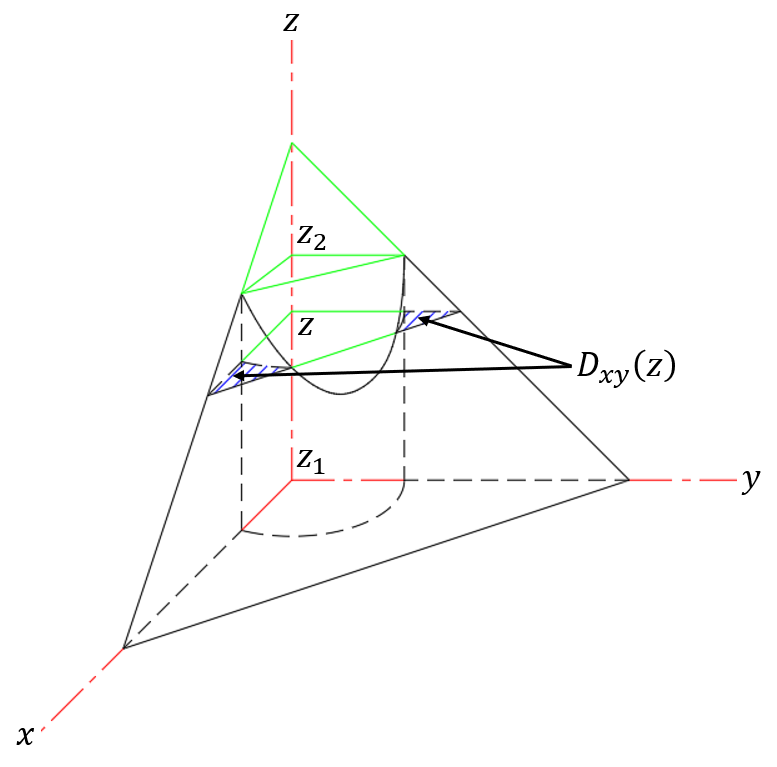
图 7.2.4: 三重积分的先二后一截面法
除了先一后二投影法以外,我们还可以利用先二后一截面法来确定积分限;如图 7.2.4 所示。
- 垂直于某一坐标轴(不妨设为轴)画平面(的等值面),确定了的坐标值,意味着最后对积分,故称为“先二后一法”;
- 上下平移平面即可得到的取值范围;
- 画的平面与区域的交面就是的积分限,为关于的函数,这实际上是积分区域关于轴的横截面,故称为“截面法”。
三重积分:柱坐标系、球坐标系
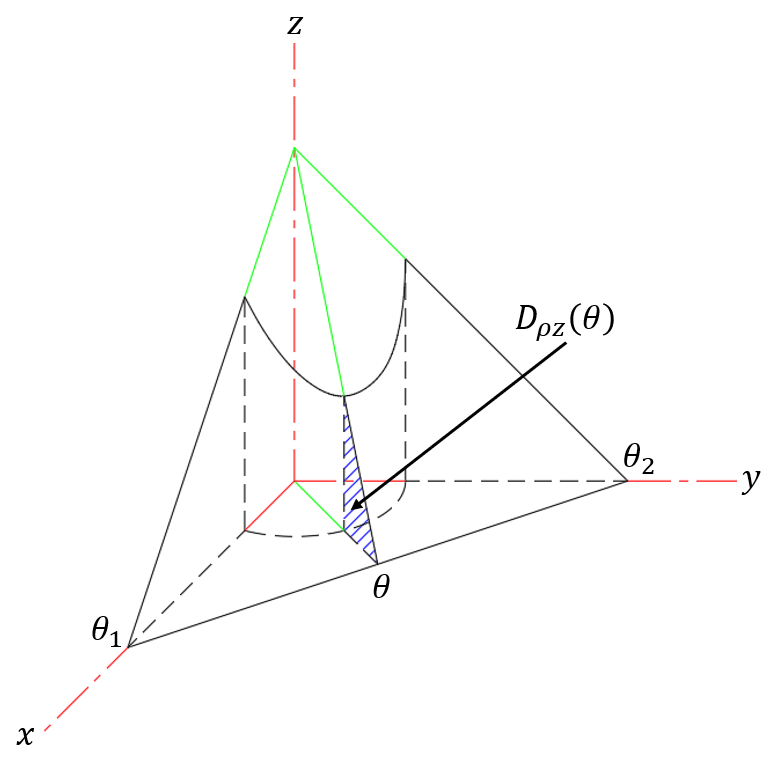
图 7.2.5: 三重积分在柱坐标系下的截面法
除了在直角坐标系中积分以外,三重积分也可以在柱坐标系、球坐标系中进行。以图 7.2.5 为例,我们可以
- 以原点为端点、为倾角画射线,画出该射线和轴构成的半平面(的等值面),确定了的值,意味着最后对积分;
- 沿轴逆、顺时针旋转半平面即可得到的取值范围;
- 画的半平面与区域的交面就是的积分限,为关于的函数。
其他情况也是类似的。
总结
尽管利用解不等式组来确定积分限的方法适用于任意空间,但在三维空间中,我们仍然可以通过画图来直观地理解积分区域的形状,从而更好地确定积分限。


