9.3 习题课讲解
9.3.1 Green公式
例 9.3.1 (习题课8·例4)
设为正向闭曲线,用Green公式计算:
解
由Green公式可得
例 9.3.2 (习题课8·例6)
设,,为直角坐标平面的第一象限中由直线、和曲线、在所围成的平面有界区域的正向边界(图8.3.3),用Green公式计算
解
由Green公式可得
这个解法需要连续可微。
例 9.3.3 (习题课8·例7)
设,在上连续,在内存在连续偏导数。若在上满足方程,为有向曲线的外单位法向量,求极限。
解
注意到
由Green公式可得
所以所求极限为。
例 9.3.4 (习题课8·例8)
设,,证明:
解
记和分别表示圆心位于原点、半径为、自然正向的圆周和圆盘,由Green公式可得
例 9.3.5 (习题课8·例9(1))
设是正值连续函数,为圆心在原点的单位圆,为的正向边界,用Green公式证明:
证明
由Green公式可得
注
重积分中积分换元的Jacobi行列式为,积分换元公式取行列式绝对值、为,这就是重积分中的对称性。
例 9.3.6 (习题课8·例10)
设在上半平面内,函数具有连续偏导数,且对任意的都有。用Green公式证明:对内的任意分段光滑的有向简单闭曲线,都有
解
设围成的区域为,由Green公式可得
注意到
令,可得
故有
例 9.3.7
记,设满足,证明:
证明
由题得
注意到
记(自然正向),则有
由积分中值定理可得使得
例 9.3.8
设为有界开集上的调和函数(记),证明:
-
(1)
-
其中、、、为的单位外法向量。
-
(2)
-
其中为以为圆心、为半径的位于中的任意圆周。
证明
(1) 注意到
原积分在处有瑕点。记(自然正向),,由Green公式可得
注意到,计算可得
由积分中值定理可得使得
由积分的三角不等式可得
因此
(2) 由(1)的结论可得
例 9.3.9
设是微分同胚,;为有界闭区域,其边界分段,。用Green公式证明:
证明
首先,我们需要证明以下引理:
引理 9.3.10
将映射为,则映射前后曲线正向是否改变取决于的符号。
引理证明
我们首先需要给“曲线正向”一个数学表述。
对于平面闭合曲线,其前向单位切向量为、外向单位法向量,轴的(正向)单位向量为,则的符号反映了的定向。设分别为与同向的切向量、法向量,则的符号反映了的定向。
设由确定(否则考虑),则为外法向量(指向增大的方向)。设可以参数化为,则为前切向量。
现考虑变换、,令,则由确定,;可以参数化为,则。记,由链式法则可得
因此、。
设,等式两端分别同乘,结合可得
记
则有
故的符号与相同。
引理证明结束,我们回到原命题。注意到
若,则映射前后曲线正向不变,故有
若,则映射前后曲线正向改变,故有
综上所述,原命题得证。
9.3.2 恰当方程与积分因子
例 9.3.11 (习题课9·例1)
求以下微分方程的通解:
-
(1)
-
-
(2)
-
-
(3)
-
-
(4)
-
解
(1) 注意到
因此通解为。如不便凑出全微分,则可先验证无旋条件
微分形式在上定义,是单连通集合,所以有原函数。计算可得
(2) 注意到
因此通解为。
(3) 注意到
因此通解为。
(4) 注意到
因此通解为。
例 9.3.12 (习题课9·例2)
求以下微分方程的通解:
-
(1)
-
-
(2)
-
-
(3)
-
-
(4)
-
-
(5)
-
解
(1) 原方程不恰当,故需要引入积分因子,其满足
亦即
令,即可由解得,此时有
因此通解为。
(2) 原方程不恰当,故需要引入积分因子,其满足
亦即
令,即可由解得,此时有
因此通解为。
(3) 这不是恰当方程。注意到
故通解为
另一种做法是利用极坐标换元,计算可得原式为
故通解为
写成直角坐标形式即为
(4) 这不是恰当方程。注意到
故通解为
若引入积分因子,其需满足
亦即
考虑微分方程组的一组线性无关的特解
从而
因此
其中是为了保证线性无关,不妨选,代回可得
于是选择为积分因子,故有
(5) 原方程不恰当,故需要引入积分因子,其满足
亦即
令,即可由解得,此时有
因此通解为。
9.3.3 第二型曲面积分
例 9.3.13 (例3)
记为锥面被柱面所截的有限部分,规定曲面的正向向下,所得的定向曲面记为。求下面两个积分的值:
-
(1)
-
-
(2)
-
解
(1) 在柱坐标系下的参数方程为
其中,即
计算可得
从而
故有
因此
(2) 直接利用楔积计算可得
或者利用其几何意义:在笛卡尔坐标系下,对应于平面中的投影面积,其系数对应于向量场的坐标,所以的系数构成向量场。向量场在点处与锥面相切,从而与法向量正交。所以所求积分(的通量)为零。
注
请注意:是锥面而不是柱面的一部分,故不为!
例 9.3.14 (例4)
记为圆柱面位于的部分(图9.3.1),外法向为正,计算曲面积分:
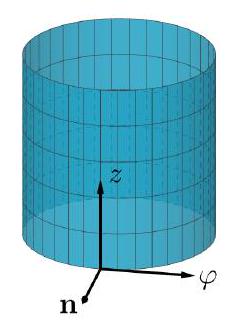
图 9.3.1: 圆柱面
解1
记向量场。根据题设,的单位正法向量,当。曲面在柱面坐标下的方程为
记,则、。于是与的单位正法向量一致。因此
解2
直接利用楔积计算可得
在点处,绕轴逆时针旋转(增加)的切向量为,沿轴上升(增加)的切向量为和曲面外法向构成右手系,所以。
例 9.3.15 (例5)
求向量场从里向外穿过第一卦限中球面时的通量。
解1
球面参数方程为
通量为
向南-向东-向上构成球面的右手系,所以符合球面从里向外。考虑到 的轮转对称(这对称性是保方向的),所以
所以
解2
用Gauss公式,取
则
因此
由对称性可得
在的三个坐标平面上,由
所以
例 9.3.16 (例6)
设为的上侧,求
解1
关于平面的反射:是一个反射变换,且使改变方向,所以上上上
类似可得上,所以
解2
注意到,计算可得
代入积分中可得
式中用到了函数奇偶性和重积分的对称性。
例 9.3.17 (例7)
设为的外侧,计算:
解
设,则且为外侧,代入积分中可得
变换保向,且保球面,所以
所以
9.3.4 曲面积分中的坐标变换
引理 9.3.18
设为正则参数曲面,是微分同胚(记都可微)且始终为正交矩阵。记,,,则对任何上的连续函数,证明:
证明
设有正则参数表示
其中为平面有界闭区域。由此得到曲面的一个参数表示
于是
故有
例 9.3.19 (例8)
设一元函数于整个实轴上连续,代表单位球面。证明Poisson公式:
这里。
证明
显然时结论成立,下设。设是正交矩阵,其第一行为。在正交变换下,,单位球面仍为单位球面。在以轴为旋转轴的柱坐标系中,球面参数方程为
由此得到
根据上述引理可知
