7.3 习题课讲解
7.3.1 确定积分区域的不等式表达、累次积分
例 7.3.1 (例1)
对连续函数,改变累次积分顺序:
解1
画出积分域的图像,如7.3.1所示,由图可知该区域可表示为
故原累次积分等于
解2
利用示性函数计算可得
其中容易被忽视的是:由解得,即。
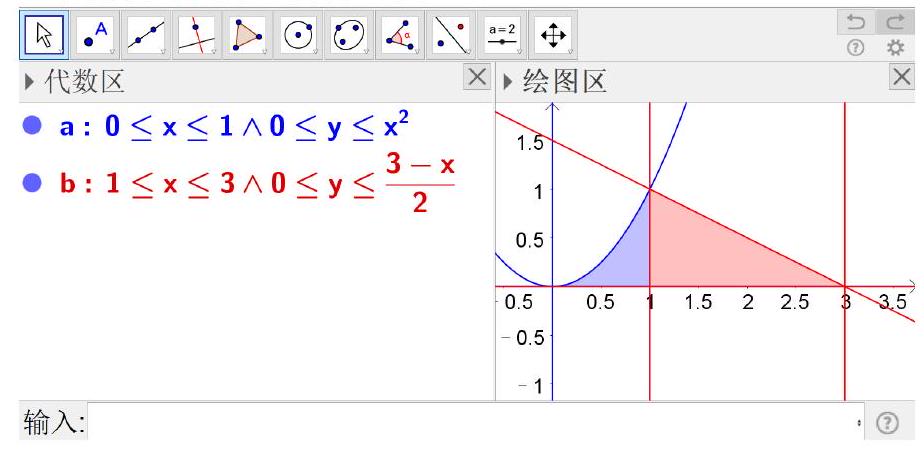
图 7.3.1: 例1的积分域
注
解2使用了示性函数(Characteristic function),其定义为
也可以简写为。示性函数有以下性质:
即它可以把集合运算变成函数的代数运算。利用示性函数,我们可以把有界区域上的积分改写为全空间上的积分,从而使得重积分(累次积分)更容易转化为(另一次序的)累次积分,如
对给定的,记;记。于是上述累次积分最终写成
通常由不等式表达。集合就是视为给定的参数,求解关于变量的不等式得到的解集。
当空间维数较高,或者区域边界很难通过画图分辨的时候,可以使用示性函数确定积分变量的范围。
例 7.3.2 (例2)
由曲面、、、、围成有界区域,写成累次积分,确定积分限,并讨论哪种顺序的累次积分形式最简单。
解
由、、知下界为、上界为,由此得到
再由和得到
因此区域可表示为
按累次积分顺序,依次写出满足的不等式:
由此得到
即 ,再结合的其他不等式得到
写成给定顺序的累次积分为
利用示性函数法(通过示性函数求解积分变量的范围):
也可以利用图形和割补法(图7.3.2):
更好的累次积分方式为
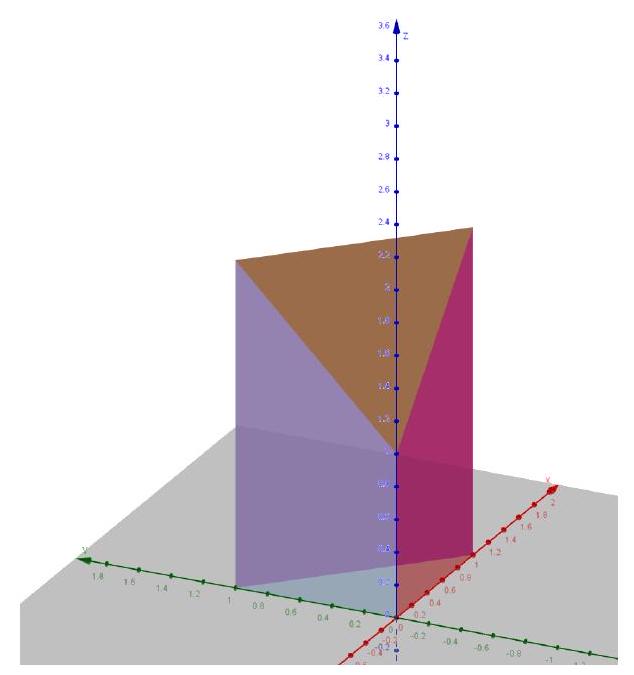
图 7.3.2: 例2的积分域
例 7.3.3 (例3)
在由曲面、、、、()围成的有界区域上,写出累次积分。如果要计算的积分,应该采用怎样的坐标系?在你选定的坐标系下,累次积分应该如何表达?
解
本题结论不唯一。如图7.3.3所示,区域1:由于
从而。由于
结合可得
故相应的累次积分为
采用以轴为对称轴的圆柱坐标系,则可表示为
区域2:由于
相应的累次积分为
采用以轴为对称轴的圆柱坐标系,则可表示为:
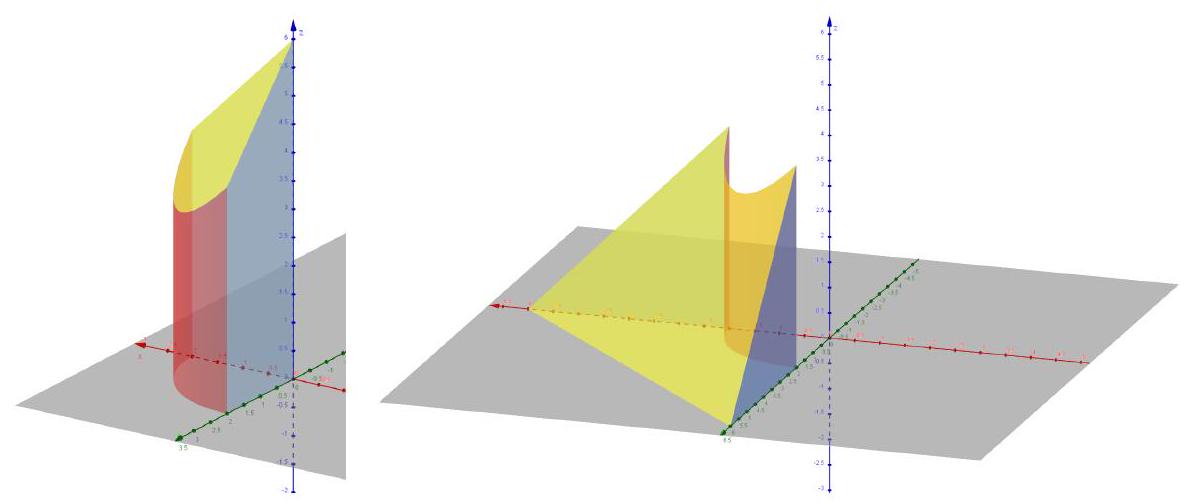
图 7.3.3: 例3的积分域
例 7.3.4 (例4)
把下列积分化为其他顺序的累次积分.可以画个图验证你的结果:
解
如图7.3.4所示,利用示性函数计算可得
另一种写法是
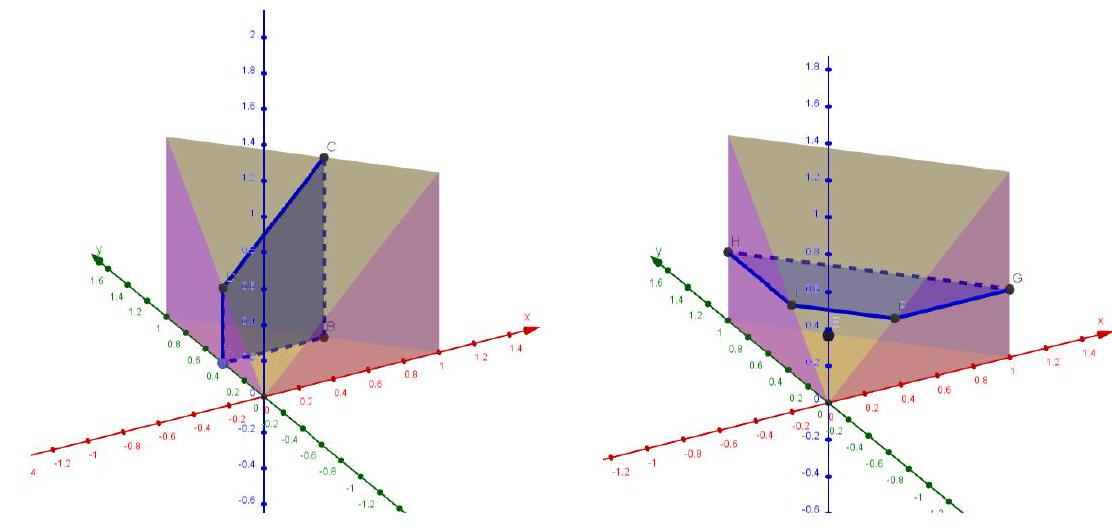
图 7.3.4: 例4的积分域
7.3.2 重积分换元
例 7.3.5 (例5)
试作适当变换,计算下列积分:
-
(1)
-
-
(2)
-
解
(1) 令、,则
计算可得
(2) 令、,则、。由于
故有,因此
计算可得
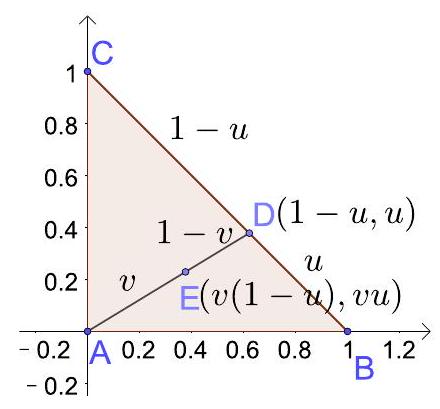
图 7.3.5: 例5(2)的积分域(任何星形区域都可以用类似办法变成矩形)
例 7.3.6 (例6)
计算:
解1
积分区域可表示为
利用柱坐标系可表示为
计算可得
解2
利用球坐标系可表示为
亦即
计算可得
例 7.3.7 (例7)
设,定义
其中()。求。
解
用柱坐标系可得
其中是的原函数,满足。用L’Hôpital法则可得
例 7.3.8 (例8)
求三重积分的值,其中
解
如图7.3.6所示,区域关于对称,被积函数中关于这个对称是奇函数,所以
球坐标系:、且,计算可得
柱坐标系(绕轴):,计算可得
你会选择直角坐标系吗?为什么?
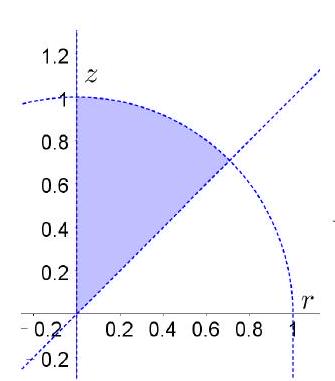
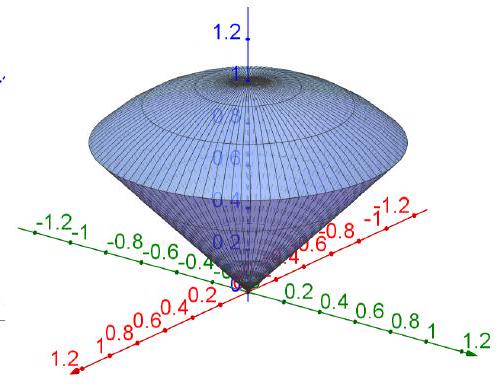
图 7.3.6: 例8的积分域
例 7.3.9 (例9)
求由曲面所围有界集的体积。
解
如图7.3.7所示,这是绕轴旋转的曲面,取柱坐标
代入曲面方程得到。为让有界,故的表示为
从而
计算可得
如果使用直角坐标系,则
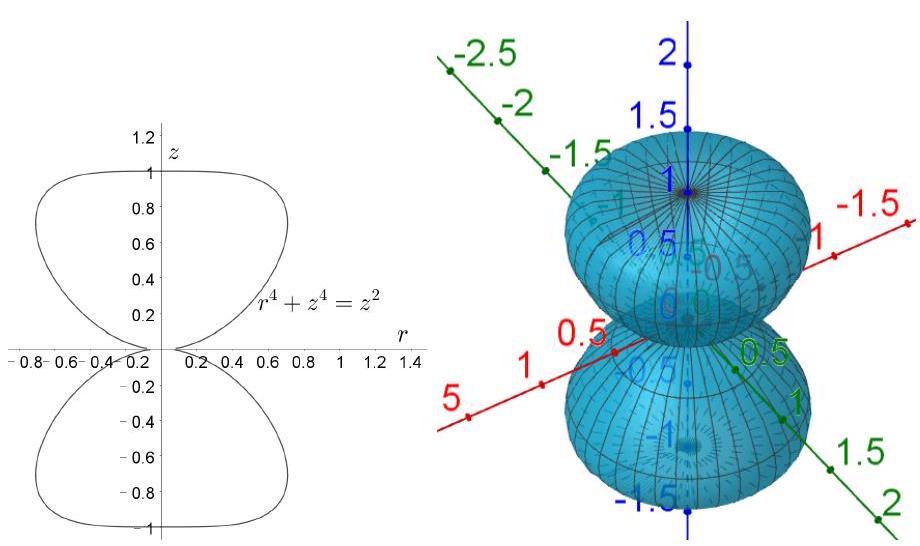
图 7.3.7: 例9的积分域
例 7.3.10 (例10)
设为实对称正定矩阵,表示三维空间的一个椭球面。证明:该椭球面所包围立体的体积为。
解
由于对称正定,因此存在可逆矩阵,使得。在线性变换下,有
注意到
于是
例 7.3.11 (例11)
求由六个平面、、所围成的有界区域的体积。
解
令
于是所求体积为
例 7.3.12 (例12)
设,。证明:
解
作正交变换
则
计算可得
例 7.3.13 (例13)
设,计算:
解1
在极坐标下,利用方向导数、微分(及微分的形式不变性)和偏导数的关系可得
因此
解2
由Green公式可得
例 7.3.14 (例14)
证明:
证明
令,则,,故
但这个做法有问题:原本不是瑕点,如此换元后反倒成为瑕点,因为Jacobi行列式不为,为此我们需要将原点单独拿出来讨论。取,则有
因此
故有
7.3.3 *重积分在概率中的应用
例 7.3.15
设为两个随机变量,其对应的概率密度函数分别为、,求、的概率密度函数。
解
设,依“概率不变原则”可得
因此
故有
其中表示和的卷积。同理可得
例 7.3.16
在正方形内独立均匀随机地取两个点,求这两点之间的距离的期望。
解
设两个点的坐标分别为和,依题意可得
这是一个很难计算的四重积分。为此我们需要换一种思路。
设、。以为例(同理),由于为均匀分布,则为三角分布,其概率密度函数为
再设,则的概率密度函数为
同理可设,则的概率密度函数为
由于相互独立,故联合密度函数,因此距离的期望为
利用极坐标换元可得
例 7.3.17
设为服从均匀分布的独立随机变量,满足
求的期望。
解
记,依据题意可得
则的分布列为
我们首先证明:
设,记,定义
则。记,注意到
因此
当时,,此时有。当时,定义
显然有,且
根据容斥原理可得
其中
因此
当时,显然有
上式为一个关于的多项式,其在时恒为,故有
因此的数学期望为
借助式,可对使用数学归纳法证明
因此
另解
的特征函数为
记,则的特征函数为
因此的概率密度函数为
注意到
结合Fourier变换的卷积性质
利用数学归纳法逐次卷积可得
当时,显然有
上式为一个关于的多项式,其在时恒为,故有
借助可得
后续解题步骤与前述解法相同。







