5.3 习题课讲解
5.3.1 计算极值
例 5.3.1 (例1)
求函数的所有极值。
解1
由
解得驻点,并计算相应的Hesse矩阵分量
整理如表5.3.1所示。
| |
Hesse矩阵 |
正定性 |
极值 |
| |
|
负定 |
极大值 |
| |
| 不定 | 鞍点 |
| | | 不定 | 鞍点 |
| |
|
正定 |
极小值 |
| |
|
正定 |
极小值 |
表 5.3.1: 函数的极值
解2
计算可得
所以对任何固定的,有
- 关于在区间上严格减;
- 在区间上严格增;
- 在区间上严格减;
- 在区间上严格增。
计算可得
所以对任何固定的,有
- 关于在区间上严格减;
- 在区间上严格增;
- 在区间上严格减;
- 在区间上严格增。
综合以上信息知,对以及,有
所以是极小值点。
类似讨论讨论可得其他临界点的极值性质。
由,所以无上界,因此没有最大值,但有最小值。
解3
配方可得
从而易得最小值点。为什么会有极大值?为什么会有鞍点?具体参考图5.3.1。
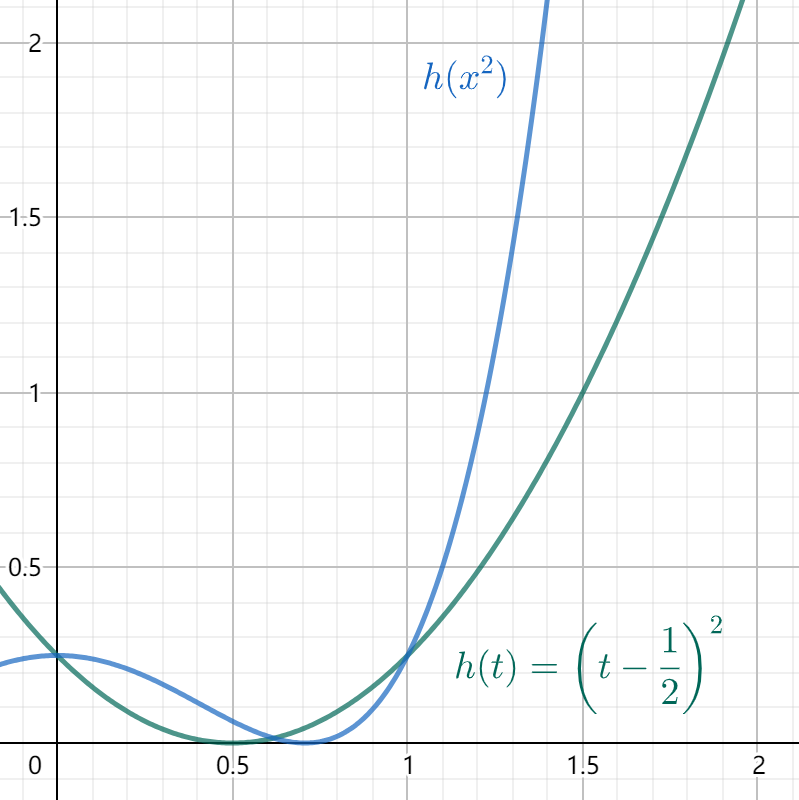
图 5.3.1: 与的图像
例 5.3.2 (例2, )
求函数的极值。
)
求函数的极值。
解
令,一元函数、在处取得极大值、在边界处取得极小值。所以在点取得最小值,在的每个点处取得最大值。
注
要善于观察函数的构造,并利用一元函数单调性的相关结论。在求解多元函数的极值时,如果定义域不是开集,则必须讨论函数在边界上的取值。
例 5.3.3 (例3, )
设由确定,求该函数的极值。
)
设由确定,求该函数的极值。
解1
虽然可以用一元二次方程的求根公式得到的显式表达式
但计算其导数过于繁琐。我们对原方程求微分可得
令,得到驻点满足的条件
方法一:利用渐近分析法:用、代入方程可得
因此是极小值。
方法二:利用二阶微分:计算可得
代入、、、可得
因此是极大值。
解2
记原方程为,它定义隐函数 的充分条件是
解1中得到的驻点都满足这个条件。于是驻点满足的方程为临界点临界点
由前5个方程解得解1中的结果。继续计算二阶导数可得
代入解得二阶导数,进而判断Hesse矩阵的类型、得到极值结论。
解3
方程配方得到
所以
所以或。易见等号可以成立。实际上,上述方程定义的曲面为双叶双曲面(图5.3.2)。
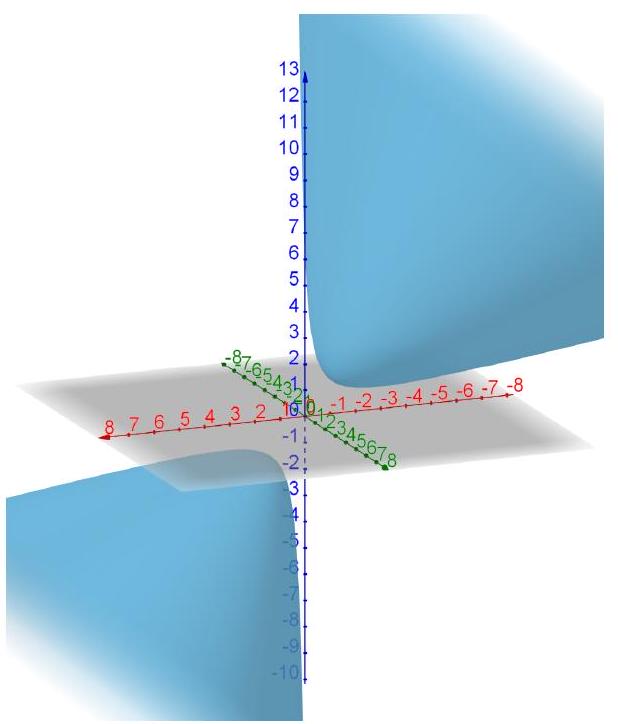
图 5.3.2: 函数的图像(双叶双曲面)
解4
配凑可得
所以或。当时,;当时,。上述不等式说明了和分别是极小值和极大值。
例 5.3.4 (例14, )
求在、、所围闭区域上的最大值。
)
求在、、所围闭区域上的最大值。
解1
连续函数在有界闭区域上取得最大值和最小值。先求开区域内的最大值,再求三条边界上的驻点,最后求所有边界两两交点的函数值。
开区域内的最大值。由驻点方程解得
只有在内,它为满足题意的驻点。计算Hesse矩阵可得
Hesse矩阵负定,故为极大值点,极大值为。
三条边界上的驻点。分情况讨论可得(计算过程略)
边界两两交点的函数值。计算可得。
综上所述,在上取得最大值,最大值点为。
解2
记
由于,此时。当或时,。所以考虑求最大值只需考虑
当(满足的条件)时,最大值为。
5.3.2 计算条件极值
例 5.3.5 (例4, )
例3可以改写为条件极值问题:
)
例3可以改写为条件极值问题:
解
构造Lagrange函数
求导可得
当、、、时,约束曲面的切向量满足
因此
因此、、是极小值。类似可得、、是极大值。
例 5.3.6 (例5, )
求函数在曲线上的最大方向导数。
)
求函数在曲线上的最大方向导数。
解
对约束条件求微分可得
曲线的切向量为
因此目标函数(沿的方向导数)为
用Lagrange乘子法计算比较繁琐,故我们借助配方给出约束曲面的一个参数化表示,即
代入可得
利用一元微积分的知识可得在(即、)时取得最大值。
例 5.3.7 (例6)
求函数沿曲线切方向的最大方向导数。
解
曲线在点处的切线方程为
曲线的切向量为
沿的方向导数为
原问题即
用Lagrange乘子法手工求解该问题显得计算比较繁琐。
考虑、(由二次型矩阵的特征方向而得),则
从而可设
得到约束曲线的参数方程
这实现了消元的目的,此时目标函数变成一元函数
对使用一元微积分的方法,得到该函数的最大值为,在、即时取得(图5.3.3)。
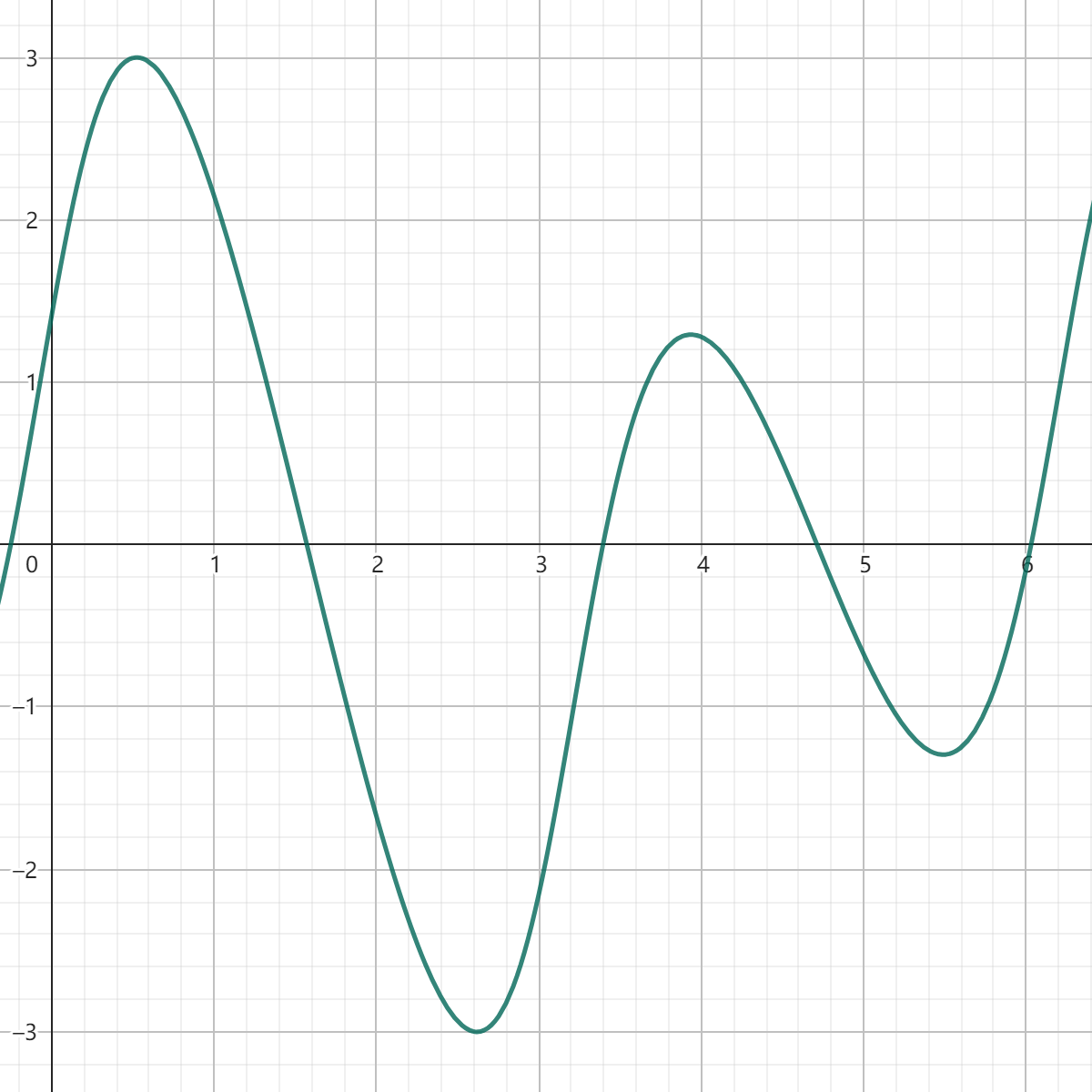
图 5.3.3: 函数的图像
例 5.3.8 (例7)
方程确定了一个曲面,求曲面上的点的坐标的取值范围。
解
原方程为关于的超越方程,即无法用有限次四则运算和开方运算来表示。我们采用下面的方法处理。
Step 0. 证明存在且唯一。
记,则对任意,有
因此对任意,关于严格增。计算可得
因此对任意,存在唯一的使得。
Step 1. 列出并求解驻点方程。
对方程求导,得到
其中
于是当且仅当
即,因此
因为
且、、,所以是的唯一零点,此时,亦即。
Step 2. 利用渐近分析法证明为极大值。
记,则
即
从而
因此
故是的极大值。
Step 3. 利用不等式放缩证明为最大值。
如果存在使得,则
矛盾。所以对任意,都有 。因此是最大值。
Step 4. 证明为的取值范围,亦即是满射。
沿直线有
对任意,取,则有,所以曲面上的点的坐标的取值范围是。
例 5.3.9 (例8, )
设为一个三角形的三条边的边长,求的取值范围。
)
设为一个三角形的三条边的边长,求的取值范围。
解
由问题的齐次性,不妨设,令
其中满足
记、(图5.3.4),则上述不等式等价于、,此时
由
知在上严格减,在上严格增,故,都有
由
知在上严格减,在上严格增,是最小值,所以。
由
知在上严格减,在上严格增,是最大值,所以。
因此的上确界在等腰三角形的腰与底的比值趋于时以极限形式取得,的最小值在等边三角形时取得,从而的取值范围为。
另解
由Cauchy-Schwarz不等式可得原式
取等号条件为。由于为三角形的三边长,每个分数值都小于1,由糖水不等式可得原式
当、时以极限形式取得上确界。故原式的取值范围为。
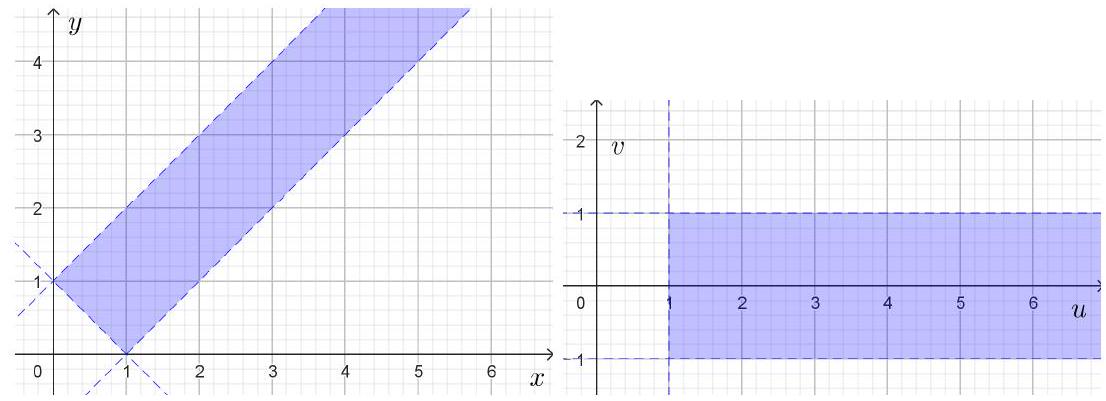
图 5.3.4: 与的取值范围
例 5.3.10 (例9)
求的最大值,其中是正数且满足。
解
记目标函数和约束函数为
因为
是有界闭凸集,是连续函数(当时,),故在上有最大值和最小值。
对,有
负定,所以在凸集上是凹函数,所以它的最小值在的(相对)边界上达到,于是的最小值在达到,最小值为。
构造Lagrange函数
则
解得
此时。是在约束条件下,在(的相对内部)中的唯一临界点,所以它是的最大值点,是的最大值。
例 5.3.11 (例11)
求原点到曲面的最短距离。
解1
原问题可化为
令
则
解得
当时,解得,此时。
当时,解得,此时无实数解。
当时,方程组无界。
当时,,此时
此时。
综上所述,原点到曲面的距离为。
解2
当时,由约束条件得到,此时。
当时,从解得,此时
由
解得、或。比较相应的的值以及,得到其中的最小值。
解3
将代入,得到
且当时,是最小距离。
解4
将代入,得到
求导可得
解得。
当时,;当时,;所以对任意关于在时取最小值。记,则
即当时,;当 时,。所以在处取得最小值。
所以在取得最小值,所求最小距离为 。
注
以上四种解法都是不完整的。
解1和解2的补救 需要证明这个问题存在最小值。目标函数在非空有界闭集
上有最小值,且最小值不大于。在中,任何函数值(如果存在)必然大于。所以此约束极值问题有最小值。另外,这个目标函数在约束条件下没有最大值,因为对任意正整数 ,点满足约束条件,它到原点距离大于。
解3和解4的补救 事实上,约束条件有个潜在的约束是,所以解4需要说明满足这个条件。有些读者可能以为把约束条件代入目标函数就万事大吉了,这里的讨论(即潜在约束的存在)说明情况并非想象的那样简单。
例 5.3.12 (例13, )
求旋转抛物面与平面的交线(椭圆)的长轴、短轴的长。
)
求旋转抛物面与平面的交线(椭圆)的长轴、短轴的长。
解1
联立曲面方程与平面方程可得
因此
代入平面方程中可得
由此知椭圆中心(对称中心)为,椭圆上的点到椭圆中心的距离满足
最大值为、最小值为。所以椭圆的长轴长为、短轴长为。
解2
设为椭圆上的两点。它们是长轴两个端点,当且仅当它们是以下问题的解(注:短轴的两个端点不是的解!)
从约束条件中尽量解出一些变量,以减少变量个数:
这是条件极值问题,接下来用Lagrange乘子法即可解出答案。另外,上述约束条件等价于
目标函数为
先用三角函数的性质化简这个表达式(降次),然后再研究它的极值和最值。
5.3.3 与极值有关的证明题(2)
例 5.3.13 (例10, )
设是由个维单位列向量组成的阶矩阵,证明,其中等号成立当且仅当是的一组单位正交基。
)
设是由个维单位列向量组成的阶矩阵,证明,其中等号成立当且仅当是的一组单位正交基。
证明1
设线性无关,此时有,否则有。作Gram-Schmidt正交化:设,且
用与上式两端内积可得
因此
上式对亦成立。设上三角矩阵满足(其中),正交矩阵,则有
故有
当且仅当所有均与对应的共线时等号成立,即是的一组单位正交基。
证明2
记
则为对称矩阵,故存在谱分解,其中为正交矩阵,为对角矩阵。由,结合AM-GM不等式可得
取等号条件为,即为正交矩阵,亦即是的一组单位正交基。
证明3
类似地可设可逆。构造Lagrange函数
记表示元素的代数余子式、,则的驻点满足
易知,否则有,此时对的第列求行列式为,与可逆矛盾。
当时,注意到
因此
故当为正交矩阵时取得极值,此时且是的一组单位正交基。
记为所有满足题设要求的矩阵构成的集合,易见为有界闭集,故函数在上有最值。由Fermat引理可知在上的最值点即为的驻点,因此在上的最大值为、最小值为,,等号成立当且仅当为正交矩阵。
例 5.3.14 (例16)
函数在有界闭区域上连续,在的边界上,在内部偏导数存在,且满足,其中是严格单调函数,且,证明。
证明1
在有界闭区域上连续,所以有最大值和最小值。
假设不恒为,则的最大值和最小值中必有一个非零。又因为在的边界上,所以的非零最值必在内某点取得,从而。由于是严格单调函数,所以,矛盾。
证明2
假设,则 。记
因为连续,,是有界闭区域,,所以。计算可得
因为,所以根据Rolle定理,存在使得
于是。由的严格单调性,。这与的定义矛盾。
例 5.3.15 (例17)
假设有连续的偏导数,在全平面除原点之外处处满足等式
证明:原点是的唯一极小值点,且满足
解
对任何,计算可得
所以严格增。所以都不是极值点。由连续性可得
所以是唯一最小值点。因此,所以,因此
例 5.3.16 (例12)
当时,求函数在球面上的最大值,这里。由此进一步证明,对于任意正实数,下述不等式成立
解
令
由
解得
从而
当时,
所以使得当时,。在包含的非空有界闭集
上连续,故有最大值。所以是在
中的最大值。于是
令即可得到
例 5.3.17 (例18)
设满足。求函数在平面第一象限里满足约束条件 的最小值。由此进一步证明Young不等式
解1
作Lagrange函数
解方程组
由方程3知,从而,因此
分情况进行讨论:
- 当时,。
- 当时,。
- 当时,。
- 当时,,总有。
注意到是含的有界闭集 在上有最小值,此最小值必然是。所以是 在约束条件下的最小值。
对所有正数,令
则、、,所以
等号当且仅当时成立。因此
等号当且仅当时成立。
解2
记,则
由此易知是的最小值点,是最小值。
例 5.3.18 (例19, )
证明对任何以及非负实数,成立Minkowski不等式
等式成立当且仅当与线性相关。
)
证明对任何以及非负实数,成立Minkowski不等式
等式成立当且仅当与线性相关。
证明1
利用Hölder不等式可得ö
其中
因此
Hölder不等式可通过加权Jensen不等式证明,等号成立当且仅当与线性相关。
证明2
当时,等式成立。假设时,不等式成立;下证时,结论成立。注意到归纳假设
所以关键在于证明当时结论成立。
令,其为关于的连续函数。考虑
若或,则或,此时要证明的不等式中等号成立。下设。因为
是有界闭集,所以连续函数在上存在最大值和最小值。不妨设,注意到
如果不是在上的最大值,则最大值点必然满足都不是零或者都不是零。
不妨设都不是零。对给定的,考虑
则条件最大值点满足
解得
从而
此时
亦即,所以
这与假设不是的最大值矛盾,因此是的最大值。
例 5.3.19 (2022春期末考试・19)
设是映射,满足
-
(a)
-
,在点处的Jacobi矩阵都是可逆矩阵;
-
(b)
-
当时,。
证明:
-
(1)
-
是满射,即,使得;
-
(2)
-
,存在有限多个使得。
证明1
(1) 令,注意到
取,使得,而在有界闭集上有最小值点,显然是上的最小值点和极小值点。由可微、结合Fermat原理知是的驻点。
对求梯度可得驻点方程为
由于可逆,故的唯一驻点满足,即是满射。
(2) 设为的原像集,我们需要证明。首先有界,否则存在满足而,这与题设(a)矛盾。再类似例2.1.5可得为闭集,故是有界闭集。,由于可逆,由逆映射定理可知和可逆映射使得
故是双射,亦即开集内有且仅有满足。
由此得到有界闭集的开覆盖。根据Heine-Borel定理(有限覆盖定理),中有界闭集的开覆盖必有有限子覆盖,其中。由于每个内只有一个点满足,所以。
证明2
(1) 我们证明非空(显然)且既开又闭,则。
,满足,由证明1(2)可知使得为双射,故,即是开集。
设满足,则使得恒成立。类似证明1(2)可知有界,故存在收敛子列使得。由于连续,故有
即是闭集。
(2) 设,由证明1(2)可知有界。采用反证法,假设,则必有聚点,否则易由有限覆盖定理得到孤立点构成的有界集必有限。由证明1(2)可知使得为双射,这与为聚点矛盾。所以。
注
证明1(1)的基本思路源自梯度下降法,即通过构造优化问题来求解方程。证明2(1)则更接近拓扑法:如果不是满射,那么中就有不属于的点;而又为闭集,故必定存在边界点,在边界点处的Jacobi矩阵必定不满秩,矛盾。




