8.2 知识点复习

8.2.1 第一型曲线积分

设曲线$\gamma \subseteq {\mathbb{R}}^m$，第一型曲面积分的一种自然的定义是$$\begin{array}{}\text{(1)}& {\int }_{\gamma }\rho (x)\mathrm{d}l=\underset{\parallel P\parallel \to 0}{lim}\sum _{k=1}^n\rho ({\xi }_k)\parallel P_k-P_{k-1}\parallel \end{array}$$ 但是这种定义并不严格，因为曲线上两个参数值相去甚远的点空间距离可能很小。

重要概念回顾

(1)

弧长：设曲线$\gamma$的参数表示为$\mathit{x}:[a,b]\to {\mathbb{R}}^m$，$\mathrm{\Pi }:a=t_0<t_1<\cdots <t_n=b$为曲线的划分，$P_k=\mathit{x}(t_k)$，则折线段的总长度为$\sum _{k=1}^n\parallel \mathit{x}(t_k)-\mathit{x}(t_{k-1})\parallel$。若$$\begin{array}{}\text{(2)}& L=\underset{\mathrm{\Pi }}{sup}\sum _{k=1}^n\parallel \mathit{x}(t_k)-\mathit{x}(t_{k-1})\parallel <+\mathrm{\infty }\end{array}$$ 则称$\gamma$为可求长曲线，$L$为曲线的弧长。

(2)

正则曲线的弧长坐标：设正则曲线$\gamma$的参数表示为$\mathit{x}:[a,b]\to {\mathbb{R}}^m$，定义弧长参数$l(t)={\int }_a^t\parallel {\mathit{x}}^{\prime }(s)\parallel \mathrm{d}s$，则$l^{\prime }(t)=\parallel {\mathit{x}}^{\prime }(t)\parallel >0$，故$l(t)$存在反函数$t(l)$，$\tilde{\mathit{x}}(l):=\mathit{x}(t(l))$称为曲线$\gamma$在弧长参数$l$下的表示。

(3)

第一型曲线积分：设$f\in \mathcal{C}(\gamma )$，定义微元弧长$\mathrm{d}l=\parallel {\mathit{x}}^{\prime }(t)\parallel \mathrm{d}t$，则$f$在$\gamma$上的第一型曲线积分定义为$$\begin{array}{}\text{(3)}& {\int }_{\gamma }f\mathrm{d}l={\int }_a^{b}f(\mathit{x}(t))\parallel {\mathit{x}}^{\prime }(t)\parallel \mathrm{d}t\end{array}$$ 在直角坐标系中有$$\begin{array}{}\text{(4)}& \mathrm{d}l=\parallel {\mathit{x}}^{\prime }(t)\parallel \mathrm{d}t=\sqrt{\sum _{i=1}^m{\left(\frac{\mathrm{d}{x}_i}{\mathrm{d}t}\right)}^2}\mathrm{d}t=\sqrt{\mathrm{d}{x}_1^2+\cdots +\mathrm{d}{x}_m^2}\end{array}$$

(4)

度规：设$\mathit{x}(t)$和$\mathit{u}(t)$为$\gamma$在两个坐标系中的参数表示，则有$$\begin{array}{}\text{(5)}& \mathrm{d}l=\sqrt{\sum _{i,j=1}^m⟨\frac{\partial \mathit{x}}{\partial u_i},\frac{\partial \mathit{x}}{\partial u_j}⟩\mathrm{d}{u}_i\mathrm{d}{u}_j}=\sqrt{\sum _{i,j=1}^m{g}_{ij}\mathrm{d}{u}_i\mathrm{d}{u}_j}\end{array}$$ 其中$G=(g_{ij}{)}_{m\times m}$为度规矩阵、$\mathrm{d}{u}_i=u_i^{\prime }(t)\mathrm{d}t$。更多信息请回顾第 2.2.7 节。

重要定理回顾

(1)

设$\lambda (\mathrm{\Pi })=\underset{1\le k\le n}{max}(t_k-t_{k-1})$，若$\underset{\lambda (\mathrm{\Pi })\to 0}{lim}L(\mathrm{\Pi })=L$，则$\gamma$为可求长曲线且$L=L(\gamma )$，即$\mathrm{\forall }\epsilon >0$，$\mathrm{\exists }\delta (\epsilon )>0$，使得对$[a,b]$的任意划分$\mathrm{\Pi }$，$\lambda (\mathrm{\Pi })<\delta (\epsilon )⟹|L(\mathrm{\Pi })-L|<\epsilon$。

(2)

若$\gamma$为${\mathcal{C}}^1$正则曲线，即$\mathit{x}\in {\mathcal{C}}^1$且${\mathit{x}}^{\prime }(t)\ne 0$，则$\gamma$为可求长曲线且$L={\int }_a^b\parallel {\mathit{x}}^{\prime }(t)\parallel \mathrm{d}t$。

(3)

第一型曲线积分的值与曲线的参数化方式无关，故为良定义的。

应用

(1)

求曲线$\gamma :r=2(1+\cos \theta )$，$\theta \in [-\pi ,\pi ]$的弧长和质心。

(2)

不同坐标系中的微元弧长公式：

• 直角坐标系：$\mathrm{d}l=\sqrt{\mathrm{d}{x}^2+\mathrm{d}{y}^2+\mathrm{d}{z}^2}$。
• 极坐标系：$\mathrm{d}l=\sqrt{\mathrm{d}{r}^2+(r\mathrm{d}\theta {)}^2}$。
• 柱坐标系：$\mathrm{d}l=\sqrt{\mathrm{d}{r}^2+(r\mathrm{d}\theta {)}^2+\mathrm{d}{z}^2}$。
• 球坐标系：$\mathrm{d}l=\sqrt{\mathrm{d}{r}^2+(r\mathrm{d}\theta {)}^2+(r\sin \theta \mathrm{d}\phi {)}^2}$。

8.2.2 第一型曲面积分

类似曲线弧长，求曲面面积的一种自然想法是使用三角形对曲面进行划分，求出这些三角形面积之和的上确界。然而早在19世纪，Schwarz证明：即便对于圆柱面，任意的三角划分可使得面积之和无上界。小平邦彦在其著作中证明：如果所有三角形的顶角都大于一个给定的正数，则上面这种做法可行。因此，我们仍需借助曲面的参数化定义曲面积分。

重要概念回顾

(1)

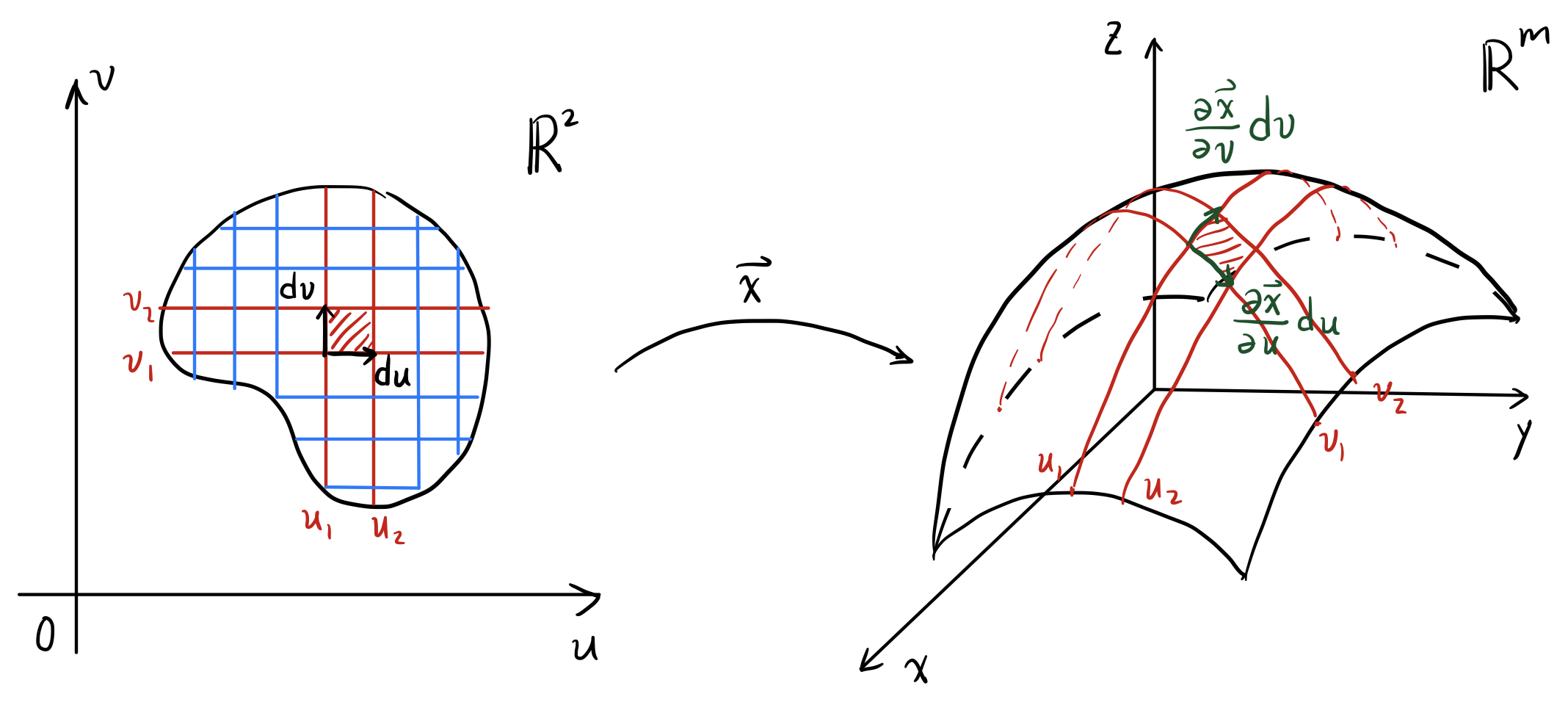
曲面的参数化：设（2维）正则曲面$\mathrm{\Sigma }\subseteq {\mathbb{R}}^m$的参数化为$\mathit{x}:D\to {\mathbb{R}}^m$，其中$D\in {\mathbb{R}}^2$，$(u,v)\in D\mapsto \mathit{x}(u,v)\in \mathrm{\Sigma }$，且$\frac{\partial \mathit{x}}{\partial u},\frac{\partial \mathit{x}}{\partial v}$在$D$上线性无关。更多内容请回顾第 4.2.3 节。

(2)

微元面积：用参数$u,v$的等值线对$\mathrm{\Sigma }$进行划分，由此得到许多微元平行四边形，其面积为$$\begin{array}{}\text{(6)}& \mathrm{d}\sigma =\Vert \frac{\partial \mathit{x}}{\partial u}\mathrm{d}u\Vert \Vert \frac{\partial \mathit{x}}{\partial v}\mathrm{d}v\Vert \sin \theta =\sqrt{\underset{E}{\underbrace{{\Vert \frac{\partial \mathit{x}}{\partial u}\Vert }^2}}\cdot \underset{G}{\underbrace{{\Vert \frac{\partial \mathit{x}}{\partial v}\Vert }^2}}-\underset{F^2}{\underbrace{{⟨\frac{\partial \mathit{x}}{\partial u},\frac{\partial \mathit{x}}{\partial v}⟩}^2}}}\mathrm{d}u\mathrm{d}v\end{array}$$

(3)

第一型曲面积分：设$f\in \mathcal{C}(\mathrm{\Sigma })$，则$f$在$\mathrm{\Sigma }$上的第一型曲面积分定义为$$\begin{array}{}\text{(7)}& {\int }_{\mathrm{\Sigma }}f\mathrm{d}\sigma ={\int }_{D}f(\mathit{x}(u,v))\sqrt{EG-F^2}\mathrm{d}u\mathrm{d}v\end{array}$$

(4)

高维曲面：设$k$维正则曲面$\mathrm{\Sigma }\subseteq {\mathbb{R}}^m$的参数化为$\mathit{x}:D\to {\mathbb{R}}^m$，其中$D\in {\mathbb{R}}^k$，$(u_1,\cdots ,u_k)\in D\mapsto \mathit{x}(u_1,\cdots ,u_k)\in \mathrm{\Sigma }$，且$\frac{\partial \mathit{x}}{\partial u_1},\cdots ,\frac{\partial \mathit{x}}{\partial u_k}$在$D$上线性无关，则微元面积的定义为$\mathrm{d}\sigma =\sqrt{detG}\mathrm{d}{u}_1\cdots \mathrm{d}{u}_k$，其中$G$为度规矩阵。

重要定理回顾 第一型曲面积分的值与曲面的参数化方式无关，故为良定义的。

应用

(1)

曲面$z=f(x,y)$的微元面积为$\mathrm{d}\sigma =\sqrt{1+\parallel \mathrm{\nabla }f{\parallel }^2}\mathrm{d}x\mathrm{d}y$。

(2)

曲线$y=f(x)>0,x\in [a,b]$绕$x$轴旋转一周得到曲面的面积为$A={\int }_{\gamma }2\pi y\mathrm{d}l$。

(3)

${\mathbb{R}}^{m+1}$中的$m$维曲面$x_{m+1}=f(x_1,\cdots ,x_m)$的微元面积为$\mathrm{d}\sigma =\sqrt{1+\parallel \mathrm{\nabla }f{\parallel }^2}\mathrm{d}{x}_1\cdots \mathrm{d}{x}_m$。

(4)

半径为$R$的$m$维球面的面积$A_m(R)$和$m$维球体的体积$V_m(R)$的关系为$A_m(R)=V_{m-1}^{\prime }(R)$。

8.2.3 第二型曲线积分

重要概念回顾

(1)

有向曲线：设$\mathit{x}:[a,b]\to \mathrm{\Omega }$（表示一种运动），$\mathit{x}(t)$表示位置（$t$为时间），路径$\gamma =\{\mathit{x}(t)\mid t\in [a,b]\}$。

(2)

第二型曲线积分：设（连续）向量场$\mathit{F}:\mathrm{\Omega }\to {\mathbb{R}}^m$，$\mathit{x}(t)$为$\gamma$上的运动，$\mathit{T}$为$\gamma$的单位前切向量，则$\mathit{F}$在$\gamma$上的第二型曲线积分定义为$$\begin{array}{}\text{(8)}& {\int }_{\gamma }⟨\mathit{F},\mathit{T}⟩\mathrm{d}l={\int }_a^b⟨\mathit{F},\frac{{\mathit{x}}^{\prime }(t)}{\parallel {\mathit{x}}^{\prime }(t)\parallel }⟩\parallel {\mathit{x}}^{\prime }(t)\parallel \mathrm{d}t={\int }_a^b⟨\mathit{F}(\mathit{x}(t)),{\mathit{x}}^{\prime }(t)⟩\mathrm{d}t={\int }_{\gamma }\mathit{F}\cdot \mathrm{d}\mathit{x}\end{array}$$ 设$\mathit{F}=(F_1,\cdots ,F_m{)}^{\mathrm{T}}$、$\mathit{x}=(x_1,\cdots ,x_m{)}^{\mathrm{T}}$，则有$$\begin{array}{}\text{(9)}& {\int }_{\gamma }⟨\mathit{F},\mathit{T}⟩\mathrm{d}l={\int }_{\gamma }\mathit{F}\cdot \mathrm{d}\mathit{x}={\int }_a^b[\sum _{i=1}^m{F}_i(\mathit{x}(t))x_i^{\prime }(t)]\mathrm{d}t={\int }_{\gamma }\omega \end{array}$$ 其中$\omega =\sum _{i=1}^m{F}_i\mathrm{d}{x}_i$为一阶微分形式。

(3)

势场：设向量场$\mathit{F}:\mathrm{\Omega }\to {\mathbb{R}}^m$，若存在$f:\mathrm{\Omega }\to \mathbb{R}$，使得$\mathit{F}=\mathrm{\nabla }f$，则称$\mathit{F}$为势场，$f$为势函数，此时一阶微分形式可表示为$$\begin{array}{}\text{(10)}& \omega =\sum _{i=1}^m{F}_i\mathrm{d}{x}_i=\sum _{i=1}^m\frac{\partial f}{\partial x_i}\mathrm{d}{x}_i=\mathrm{d}f\end{array}$$

(4)

保守场：设向量场$\mathit{F}:\mathrm{\Omega }\to {\mathbb{R}}^m$，若$\mathit{F}$在任意从$A$到$B$的${\mathcal{C}}^1$路径$\gamma$上的第二型曲线积分为零，则称$\mathit{F}$为保守场。

(5)

无旋场：设向量场$\mathit{F}:\mathrm{\Omega }\to {\mathbb{R}}^m$，若$\frac{\partial F_i}{\partial x_j}=\frac{\partial F_j}{\partial x_i}$对任意$1\le i<j\le m$成立，则称$\mathit{F}$为无旋场。

重要定理回顾

(1)

Newton-Leibniz公式：对于$\mathrm{\Omega }$中的任意从$A$到$B$的${\mathcal{C}}^1$路径$\gamma$，都有$$\begin{array}{}\text{(11)}& {\int }_{\gamma }\mathrm{\nabla }f\cdot \mathrm{d}\mathit{x}=f(B)-f(A)⟺{\int }_{\gamma }\mathrm{d}f=f(B)-f(A)\end{array}$$

(2)

势场是保守场。区域（连通的开集）上的保守场是势场。

(3)

势场是无旋场。单连通区域（区域中的任意连续闭曲线可连续变换为点）上的无旋场是保守场。

应用

(1)

力做的功：$W={\int }_{\gamma }\mathit{F}\cdot \mathrm{d}\mathit{x}$。

(2)

流场的环量：${\oint }_{\gamma }\mathit{F}\cdot \mathrm{d}\mathit{x}$。

(3)

平面流场的通量：设$\gamma$为平面上的闭合曲线，$\mathit{T},\mathit{n}$为$\gamma$的单位前切向量、外法向量，$\mathit{k}$为平面的单位法向量且$\mathit{T},\mathit{k},\mathit{n}$构成右手坐标系，则流场$\mathit{F}$在$\gamma$上的通量为$$\begin{array}{}\text{(12)}& {\int }_{\gamma }\mathit{F}\cdot \mathit{n}\mathrm{d}l={\int }_{\gamma }\mathit{F}\cdot (\mathit{T}\times \mathit{k})\mathrm{d}l={\int }_{\gamma }(\mathit{k}\times \mathit{F})\cdot \mathrm{d}\mathit{x}\end{array}$$

(4)

设$\gamma$为球面$x^2+y^2+z^2=R^2$与平面$x+y+z=0$的交线，其前向通过右手定则确定：法向量沿$+z$轴方向，计算：${\oint }_{\gamma }z\mathrm{d}x+x\mathrm{d}y+y\mathrm{d}z$。

(5)

设$\gamma \subseteq {\mathbb{R}}^2$为平面自然正向（逆时针，一般记作${\gamma }^{+}$）的简单闭曲线，则$\gamma$围成区域的面积为$$\begin{array}{}\text{(13)}& A(\gamma )={\oint }_{{\gamma }^{+}}x\mathrm{d}y={\oint }_{{\gamma }^{+}}-y\mathrm{d}x=\frac{1}{2}{\oint }_{{\gamma }^{+}}(x\mathrm{d}y-y\mathrm{d}x)\end{array}$$ 在极坐标系下，有$$\begin{array}{}\text{(14)}& A(\gamma )=\frac{1}{2}{\oint }_{{\gamma }^{+}}{r}^2\mathrm{d}\theta \end{array}$$

(6)

求势函数的方法：凑全微分，或利用$f(B)=f(A)+{\int }_{\gamma }\mathit{F}\cdot \mathrm{d}\mathit{x}$，其中$\gamma$为从$A$到$B$的任意一条路径。利用以上方法证明：$\mathit{F}(\mathit{x})=-\frac{\mathit{x}}{\parallel \mathit{x}{\parallel }^3}$的势函数为$f(\mathit{x})=\frac{1}{\parallel \mathit{x}\parallel }+C$。

(7)

计算：${\int }_{\gamma }[({\mathrm{e}}^y+\sin x)\mathrm{d}x+(x{\mathrm{e}}^y-\cos y)\mathrm{d}y]$，其中$\gamma$为$(x-\pi {)}^2+y^2={\pi }^2$上的圆弧，从$(0,0)$逆时针旋转到$(\pi ,\pi )$。

(8)

计算：${\int }_{\gamma }[(x^2-yz)\mathrm{d}x+(y^2-zx)\mathrm{d}y+(z^2-xy)\mathrm{d}z]$，其中$\gamma :t\mapsto (a\cos t,a\sin t,bt)$，$t\in [0,2\pi ]$，$a,b>0$。

(9)

容易证明$\mathit{F}={(\frac{-y}{x^2+y^2},\frac{x}{x^2+y^2})}^{\mathrm{T}}$是${\mathbb{R}}^2\setminus \{\mathbf{0}\}$（非单连通）上的无旋场，然而${\oint }_{\partial B(\mathbf{0},a)}\mathit{F}\cdot \mathrm{d}\mathit{x}={\int }_0^{2\pi }\mathrm{d}\theta =2\pi \ne 0$，故$\mathit{F}$不为${\mathbb{R}}^2\setminus \{\mathbf{0}\}$上的保守场。在单连通区域${\mathbb{R}}^2\setminus \{(x,0)\mid x\le 0\}$上，则可以证明$\mathit{F}$有势函数$f(x,y)=\arg (x+\mathrm{i}y)$。

注

(1)

这里$\mathit{x}(t)$不是$\gamma$的参数化！$\gamma$为静态对象，而$\mathit{x}(t)$是动态运动，其可在$\gamma$上作往复运动等。

(2)

无旋场不一定是保守场，见应用(9)。