10.1 知识点复习
10.1.1 向量场的旋度和散度、Gauss公式、Stokes公式
重要概念回顾
-
(1)
-
散度:空间向量场的散度定义为
-
(2)
-
旋度:空间向量场的旋度定义为
-
(3)
-
楔积与外微分的运算法则:设为阶微分形式、为阶微分形式,则
- ,。
- 。
- 。
- 。
重要定理回顾
-
(1)
-
Gauss公式的物理表述:设为空间闭区域,其边界分片且法向为曲面外向,为向量场,则有
-
(2)
-
Stokes公式的物理表述:设为可定向曲面,其边界为分段曲线且前向为曲面法向,为向量场,则有
-
(3)
-
Gauss公式和Stokes公式的数学表述:,其中为一阶或二阶微分形式,称为广义Stokes公式。
-
(4)
-
Gauss公式的展开形式:
-
(5)
-
Stokes公式的展开形式:
应用
-
(1)
-
散度的物理定义:。
-
(2)
-
旋度的物理定义:,其中表示以为圆心,为法向量,半径为的圆盘。
注
广义Stokes公式涵盖了Newton-Leibniz公式、Green公式、Gauss公式、Stokes公式等,它联系了彼此相关的两个不同维数的几何对象上的积分:当几何对象升高一维时,被积分的微分形式就通过外微分(求导)运算提高一阶,几何对象的维数与被积分的微分形式的阶数一致。其中,Newton-Leibniz公式
这里分别是区间在左右两个端点(边界)处的单位外法向量(沿着数轴)。
一方面,我们可以利用这些公式对积分“降维”;另一方面,我们使用这些公式,把曲线曲面上的积分变成高维欧氏空间上的积分。此外,这些公式还把不同的物理量联系在一起,如反映了区域内的向量场的散度、旋度(微观性质)和边界上的通量、环量(宏观性质)的联系。
10.1.2 曲线、曲面积分小结
王兆臻学长总结了曲线、曲面积分的所有重要知识点,大家可以参考。
10.1.3 *曲面坐标系(2)
设为正交曲面坐标系中的一点,方向的单位向量为,则
设,则可表示为
散度的物理定义和计算方式如图10.1.1所示。由图可知,通过微元长方体中与垂直的两个表面的通量为
其余表面同理。由Gauss公式可得
因此
取,可得Laplace算子在正交曲面坐标系中的展开为
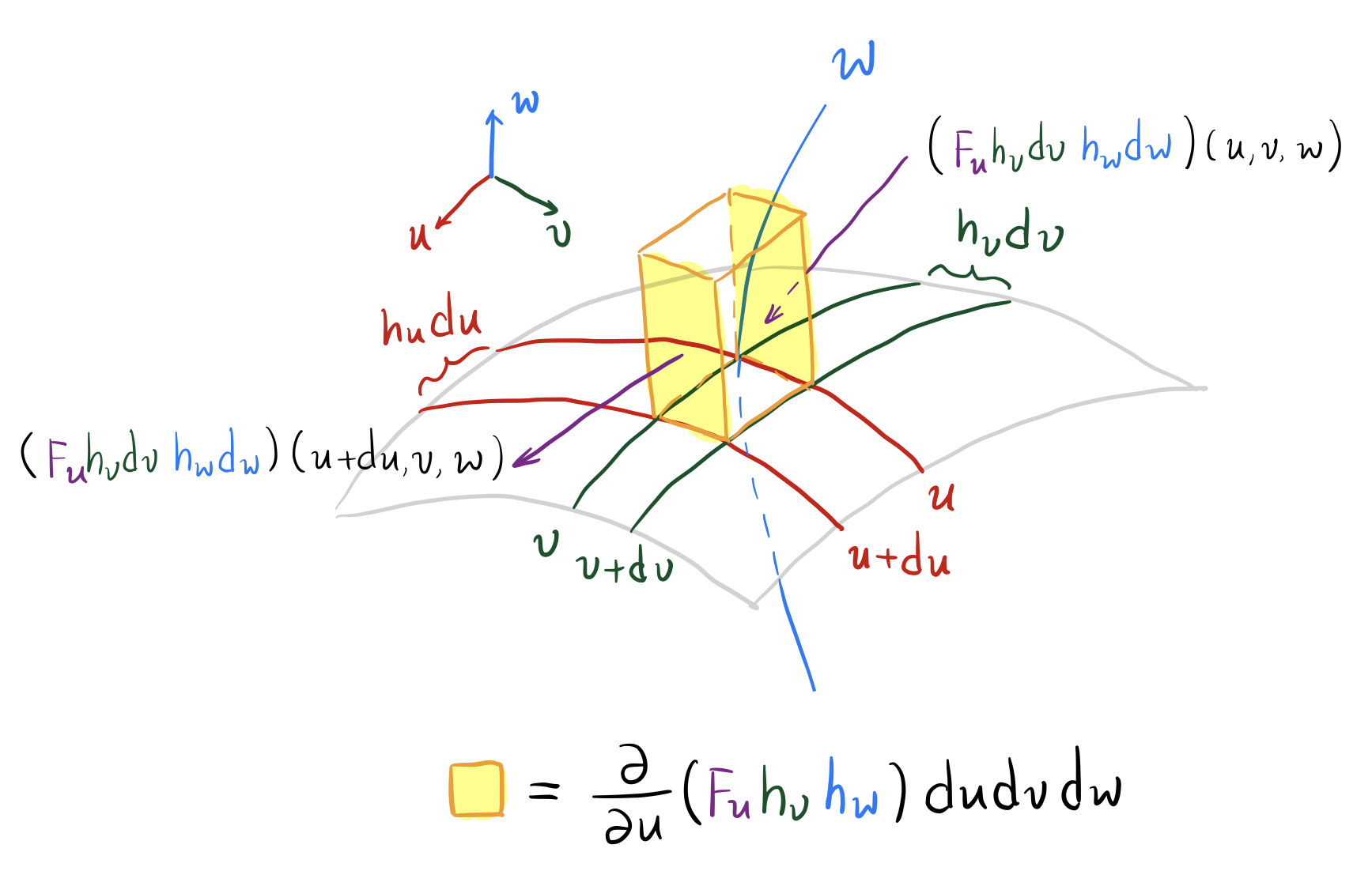
图 10.1.1: 散度的物理定义和计算方式
旋度的物理定义和计算方式如图10.1.2所示。由图可知,通过与垂直的微元长方形边界的前向环量为
由Stokes公式可得
其余方向同理。因此
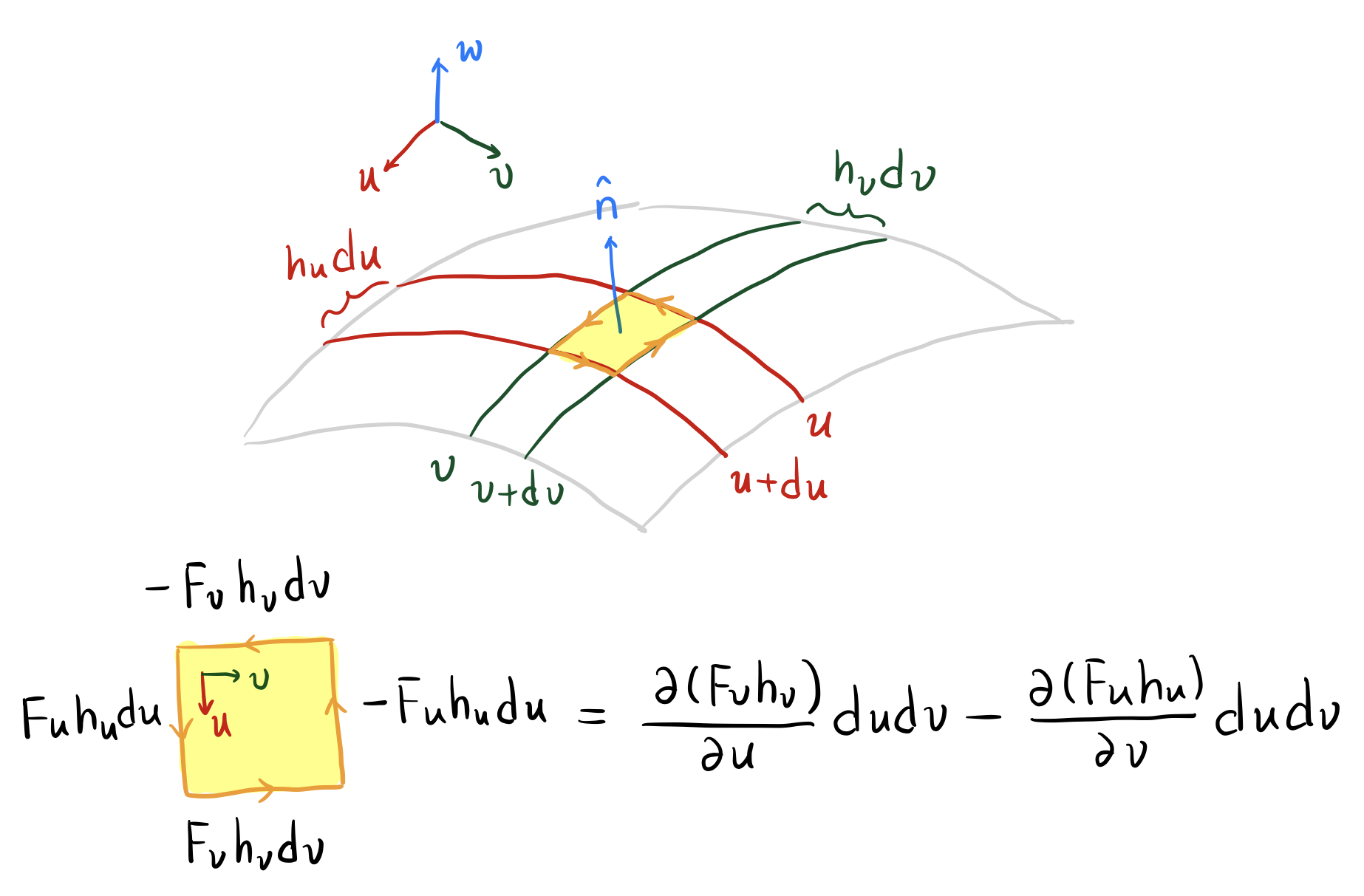
图 10.1.2: 旋度的物理定义和计算方式
10.1.4 *向量分析
设,,算符满足以下运算公式:
-
-
-
-
-
-
-
以上公式都可以用直角分量展开直接证明,但只要我们正确地考虑到算符(包括、)的特性,就可以把上述公式简单地“写”出来,例如:
- 计算:作为微分算符,既要作用在上、也要作用在上,因此有
- 计算:作为微分算符,既要作用在上、也要作用在上,因此有
然而不是正确的写法,需要将其改为,最终有
计算同理,但需要严格遵守“标量在前、向量在后”的规则。
- 计算:利用向量的混合积公式
可得到
移动的位置,可使其分别作用在和上;但是并不是正确的写法,需要将其改为。最终的结果是上述两部分之和,即
- 计算:只考虑作用在的部分,利用向量的向量积公式
可得到
并不是作用在上的,需要将其改为,其中是一个复合算符,既可以作用在标量函数上、又可以作用在向量函数上。再考虑其作用在的部分,同理需要将改为。最终的结果是上述两部分之和,即
- 计算:只考虑作用在的部分,需要反向利用
将修正为,得到不变
再考虑,最终有
- 计算:这里只有一个向量函数,直接利用向量的向量积公式可得
10.1.5 *Helmholtz分解
定理 10.1.1
(Helmholtz分解)设为有界开区域,向量场且,则可以分解为无旋场与无源场之和,即
其中
注
对于线性向量场,,。

